МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра Автоматики
Индивидуальное задание № 2 по курсу
«Системы автоматической оптимизации»
Факультет: АВТ
Группа: ААМ–11
Студент: Кутузова И.В. Преподаватель: Французова Г.А.
Вариант №11
Новосибирск
2011
Задание
Рассчитать оптимальное управление для объекта, математическая модель которого имеет вид:
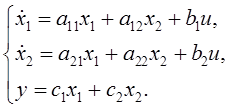
Известны ограничение на управляющее воздействия, ![]() , начальная
, начальная ![]() и
конечная точки
и
конечная точки ![]() . Заданы требования к качеству
процесса в виде критерия оптимальности
. Заданы требования к качеству
процесса в виде критерия оптимальности 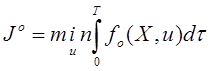 и
длительности процесса
и
длительности процесса ![]() .
.
Численные значения параметров представлены в таблице 1.
Таблица 1. Исходные данные.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
-3 |
0 |
0 |
1 |
1 |
2 |
1 |
0 |
|
1 |
|
Расчет
Математическая модель объекта:
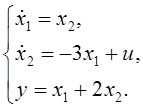
Для
расчёта оптимального регулятора воспользуемся принципом максимума Понтрягина.
Запишем расширенный вектор состояния: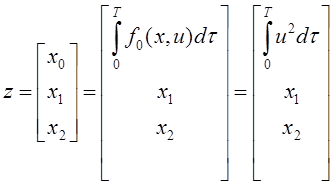
Вектор правых частей: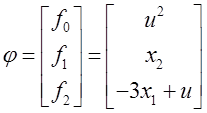
Вектор
сопряжённых координат:![]()
Гамильтониан:![]()
Из условия максимума гамильтониана определяем оптимальное управление как функцию сопряжённых координат:
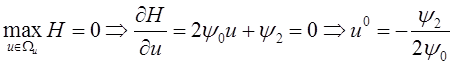
Сформируем систему дифференциальных уравнений для нахождения сопряжённых координат:
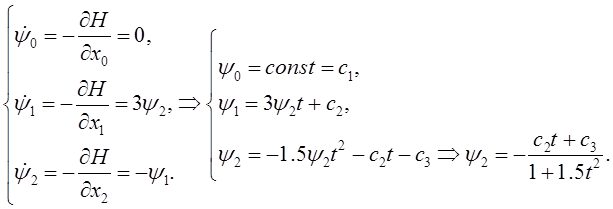
В результате оптимальное управление принимает вид:
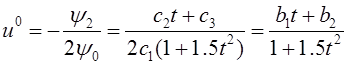 .
.
Коэффициенты bi определим, решая краевую задачу. С этой целью запишем уравнение замкнутой системы
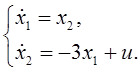
Определим решение для переменных состояния в виде
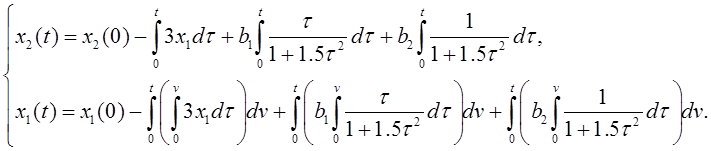 (1)
(1)
Поскольку зависимость x1(t) неизвестна, невозможно найти решение системы уравнений.
Моделирование системы
Решим задачу методом подбора.
Найдем зависимость переходных процессов х1(t) и х2(t) от b1 и b2.
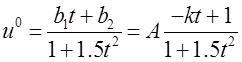
1. Подбираем k таким, чтобы x2(T)=0.
2. Подбираем Aтаким, чтобы x1(T)=1.
В результате
получили. ![]()
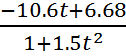
Модель системы представлена на рис.1.
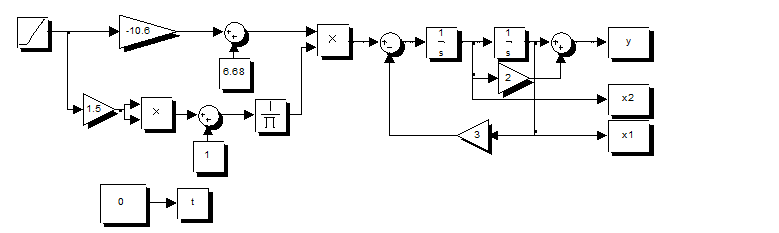
Рис.1. Модель системы
Результаты моделирования, представленные на рис.2,3 иллюстрируют, что конечные значения переменных состояния соответствуют заданным (x1(T)=1, x2(T)=0 при T=1).


![]()

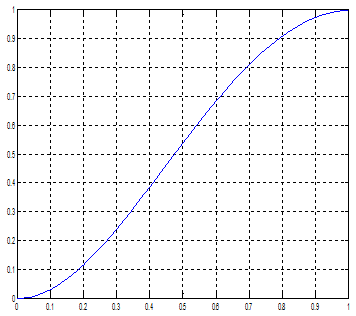
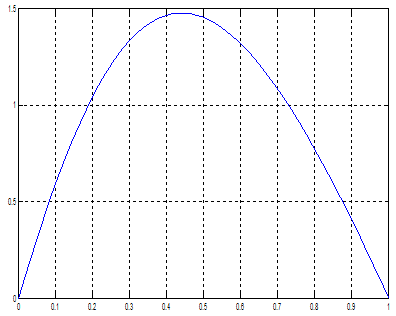
Рис.6. Переходный процесс x1(T) Рис.7. Переходный процесс x2(T)
Вывод
Для решения задачи поиска оптимального управления нельзя применить метод динамического программирования, поскольку время перехода в заданное состояние ограничено(T=1). Решить задачу с помощью принципа максимума Понтрягина тоже нельзя, так как в сформированной системе уравнений (1) неизвестна функция x1(t).
Оптимальное
управление для заданного объекта по заданному критерию было найдено методом
подбора с помощью анализа влияния управляющего воздействия и его коэффициентов на
переходные процессы x1(T)
и x2(T).
Оптимальное управление имеет вид ![]()
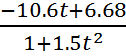 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.