(8) Здесь параметр C играет роль весового коэффициента, определяющего, какому из соотношений (7) мы отдаем предпочтение. Параметр T, имеющий размерность времени, характеризует желаемое время затухания колебаний ротора.
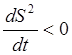 Условие выхода системы на желаемую траекторию и дальнейшего
скольжения вдоль
нее имеет вид
Условие выхода системы на желаемую траекторию и дальнейшего
скольжения вдоль
нее имеет вид
![]() (9)
или
(9)
или
Совместное использование условий (7) и уравнения (8) преобразует условие (9) в требование
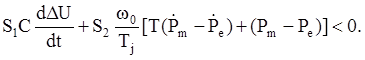
(10)
Уравнения (1) - (6) позволяют привести условие (10) к виду S0 + SaUa + SmUm < 0, (11) где S0, Sa, Sm являются функциями токов статора и возбуждения, напряжения на шинах генератора и отклонения частоты .Именно соотношение (11) позволяет сформулиро-вать правила для нечеткого контроллера, формирующего стабилизирующие сигналы Ua и Um и принимающего решение о вмешательстве в происходящие процессы.
Подход, использованный в настоящей работе, основан на следующих положениях. При незначительных отклонениях от номинальных величин напряжения на шинах и частоты генератора управление осуществляется от традиционных линейных регуляторов возбуждения генератора и скорости первичного двигателя. В области значительных отклонений параметров процессов от заданных величин вырабатываются дополнительные управляющие воздействия, обеспечивающие скользящий режим системы. По мере возвращения ее к номинальному режиму степень воздействия дополнительных сигналов уменьшается. Совместные действия основных регуляторов и дополнительных контроллеров координируются нечеткими арбитрами FLCA и FLCM ( на рис. 1 и 2 представлены предложенные структурные схемы регуляторов возбуждения и угловой скорости соответственно).
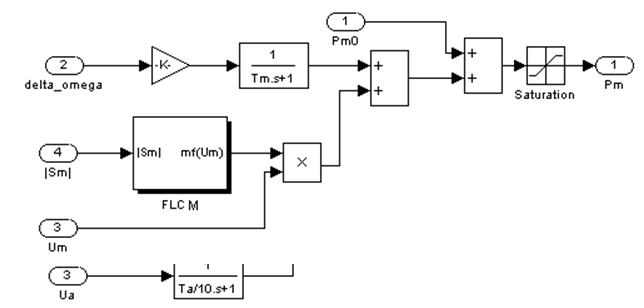 |
Рис. 2.
Функции принадлежности лингвистических переменных Sa, Sm, mf(Ua), mf(Um) изображены на рис. 3. База правил нечеткого арбитра контура управления возбуждением имеет следующий вид
R1: if |Sa| is S then mf(Ua) is ZE,
R2: if |Sa| is B then mf(Ua) is P, а контура управления скоростью R1: if |Sm| is S then mf(Um) is ZE,
R2: if |Sm| is B then mf(Um) is P.
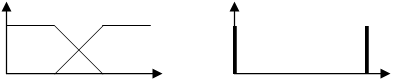 a1
a2
a1
a2
FLCA 350 650
0 a1 a2 x 0 1 mf(U) FLCM 20 40
Рис. 3.
Результаты моделирования динамического отклика одномашинной энергосистемы с шиной бесконечной мощности, управляемой с использованием предложенного подхода, представлены на рис. 4 и 5. Нами промоделирована следующая последовательность трехфазного короткого замыкания на землю:
1) 0.0 =< t < 8.04 с. - работа на две параллельные линии передачи,
2) 8.04 =< t < 8.14 с. - трехфазное короткое замыкание на одной из линий,
3) 8.14 =< t < 20 с. - отключение поврежденной линии, передача по второй линии.
 |
 |
 |
||
![]()
![]()
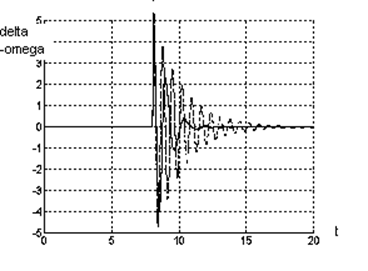
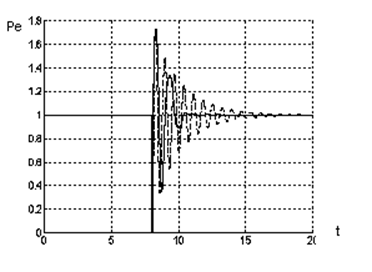
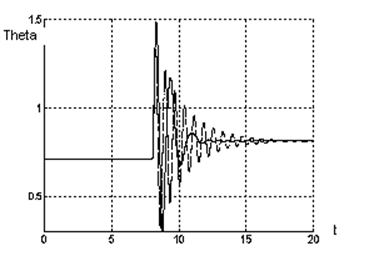
![]() На рис. 4 приведены отклики
угла ,производной угла ,электрической мощности Pe. Рис. 5
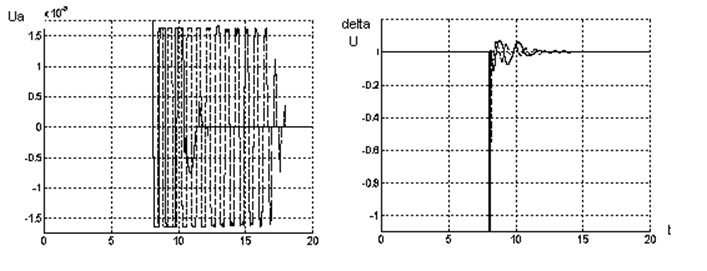
представляет поведение напряжения возбуждения Uf , отклонения напряжения на шинах
генератора и дополнительных управляющих сигналов Uа и Um ( штриховые линии на рисунках
относятся к процессам в системе с традиционными регуляторами, сплошные - к
процессам в системе с дополнительными управляющими сигналами ). Результаты
моделирования подтверждают возможность быстрого восстановления параметров
системы после аварийного режима в случае использования нечеткого контроллера
для реализации скользящего режима.
На рис. 4 приведены отклики
угла ,производной угла ,электрической мощности Pe. Рис. 5
представляет поведение напряжения возбуждения Uf , отклонения напряжения на шинах
генератора и дополнительных управляющих сигналов Uа и Um ( штриховые линии на рисунках
относятся к процессам в системе с традиционными регуляторами, сплошные - к
процессам в системе с дополнительными управляющими сигналами ). Результаты
моделирования подтверждают возможность быстрого восстановления параметров
системы после аварийного режима в случае использования нечеткого контроллера
для реализации скользящего режима.
 |
Таблица
|
Xd=1.1 |
Xq=1.0 |
Xe=0.3 |
|
|
Ta=0.1 |
Ka=40.0 |
Tm=2.0 |
Km=10.0 |
|
Pm0=1.0 |
Omega_0=314 |
C=1.0 |
Заключение. В работе для повышения динамической устойчивости энергосистемы предложен метод совместного управления регуляторами возбуждения генератора и угловой скорости первичного двигателя путем организации скользящего режима. С использованием нечетких арбитров реализована коррекция управляющих воздействий традиционных линейных регуляторов.
Список литературы.
1. В. И. Уткин. Скользящие режимы в задачах оптимизации и управления. М., Наука, 1981.
2. T. Senjyu, A. Miyazato, K. Uezato. Improvement of Power System Stability by Cooperative Fuzzy Controller. Proceedings of the International Conference on Electrical Engineering. Aug. 12-15, Beijing, 1996, China, 1996, vol. 1, pp. 328-332.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.