Рассчет и исследование с помощью моделирования в среде MATLAB системы экстремального регулирования (с учетом необходимых оценок производных) для объекта

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматики

Расчетно-графическая работа №1

по курсу

Оптимальные и адаптивные системы

Факультет: АВТ

Группа: ААМ-10

Студент:                                                                                                       Преподаватель:

Ливенец Д.                                                                                       Французова Г.А. 

Вариант: 7    

Дата выполнения:

Отметка о защите:

Новосибирск, 2010

Цель работы: рассчитать и исследовать с помощью моделирования в среде MATLAB систему экстремального регулирования (с учетом необходимых оценок производных) для объекта, математическая модель которого имеет вид:

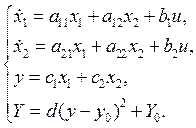
Известны ограничения на переменные состояния и управляющие воздействия: , , . Заданы требования к качеству процесса выхода на экстремум в виде следующих оценок:  и . Численные значения параметров представлены в таблице 1.

Таблица 1

Параметр
Значение	0	-2	2	3	0	8	1	1
Параметр								, %
Значение	2	1	2	20	60	500	3	0

Решение:

Рассмотрим систему уравнений, описывающих объект в следующем виде:

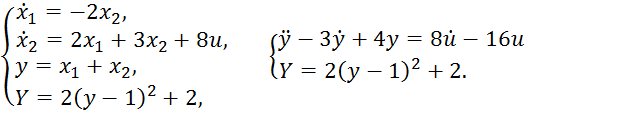
Так как в данном случае относительный порядок объекта равен единицы, то закон управления выглядит следующим образом:

где  – параметр регулятора, а  – желаемое уравнение. Сформируем желаемое уравнение исходя из заданных требований к системе. На основании требований к динамике процессов выберем корень характеристического уравнения .

Учитывая требования к статике

получим

Преобразуем уравнение с учетом градиента:

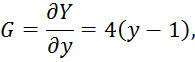
Для выбора параметра регулятора  запишем уравнение объекта в следующем виде:

где ,  .

Параметр  выбираем из условия , учитвая что , выберем:

Проверим условие разрешимости задачи синтеза:

Таким образом, ресурса управления достаточно для реализации сформированного желаемого уравнения.

Так как производная выходного сигнала недоступна для измерения, то вместо точного значения производной будем пользоваться ее оценкой:

где  – оценка производной выходного сигнала получаемая с помощью дифференцирующего фильтра.

Для оценки производной выходного сигнала воспользуемся дифференцирующим фильтром. При отсутствии помех измерения можно воспользоваться фильтром первого порядка:

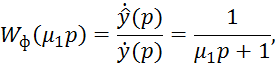
где  – постоянная времени дифференцирующего фильтра, выбираемая из условия разделимости движений:

Для получения оценки градиента  будем использовать фильтр оценки частной производной, модель которого имеет вид:

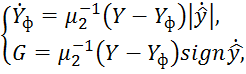
где  – постоянная времени дифференцирующего фильтра, выбираемая из условия разделимости движений:

Результаты моделирования:

Структурная схема системы поиска экстремума показана на рис. 1. Моделирование проводилось при  , . Графики переходных процессов , а так же траектория движения системы на плоскости , представлены на рис. 2- 6 соответственно.

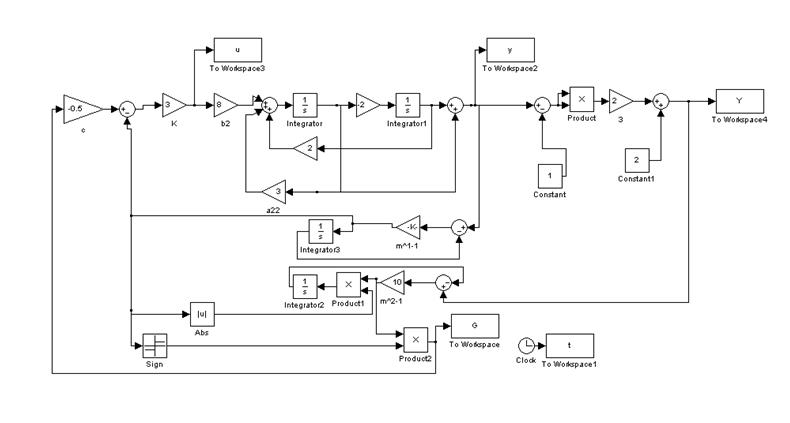
Рис. 1. Структурная схема системы поиска экстремума

Поскольку корень числителя данной передаточной функции исходного объекта положительный и находится в правой полуплоскости, то объект будет неустойчив, значит не выполняется условие разрешимости задачи синтеза. Следовательно, такой объект нельзя стабилизировать.

Возьмем объект с измененными параметрами, которые удовлетворяют условиям:

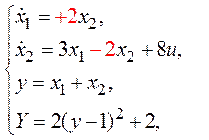
Результаты моделирования этого объекта при тех же самых начальных условиях показаны на рис.7-11.

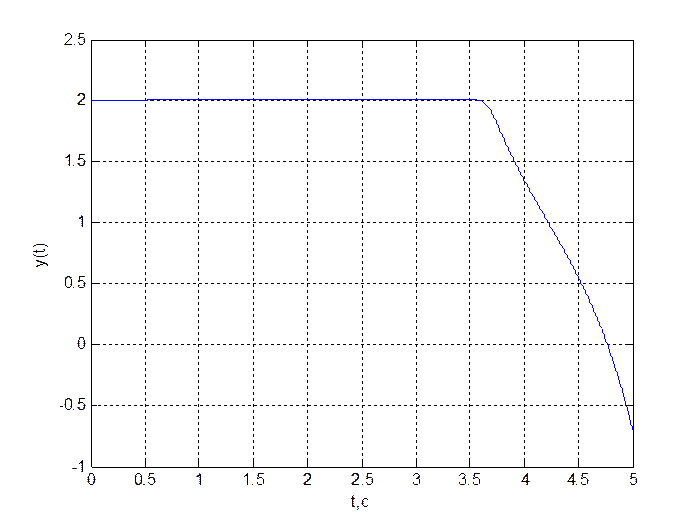
Рис. 2. График переходного процесса  

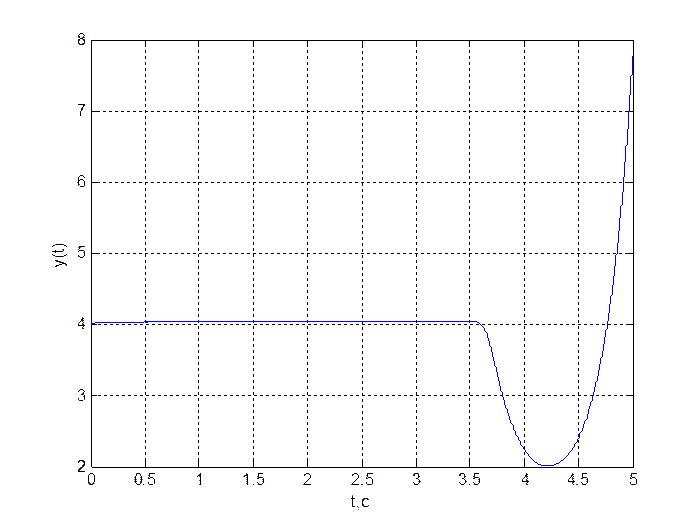
Рис. 3. График переходного процесса  

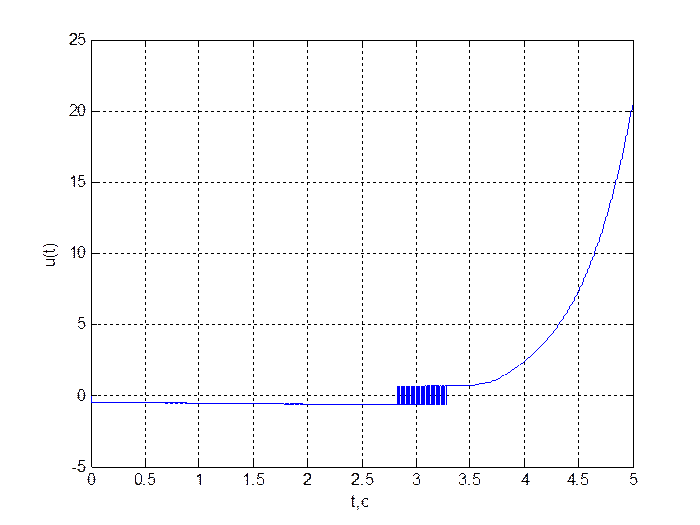
Рис. 4. График переходного процесса  

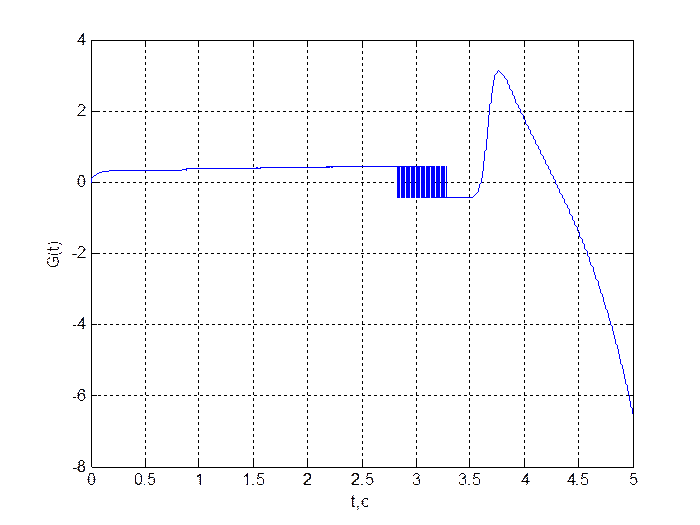
Рис. 5. График переходного процесса  

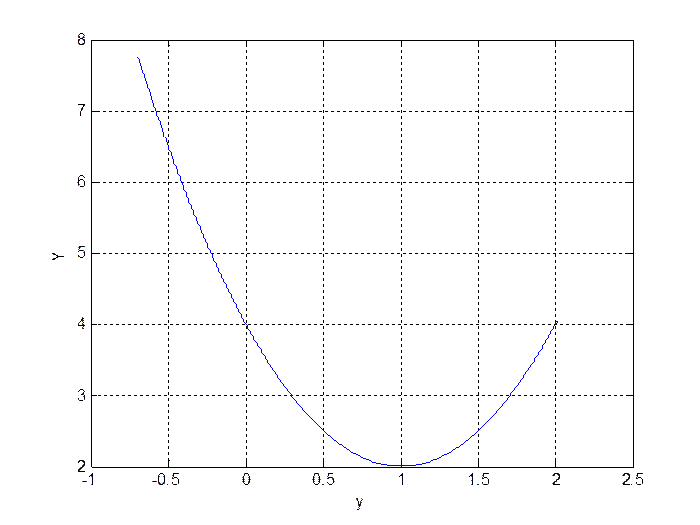
Рис. 6. Траектория движения системы на плоскости  

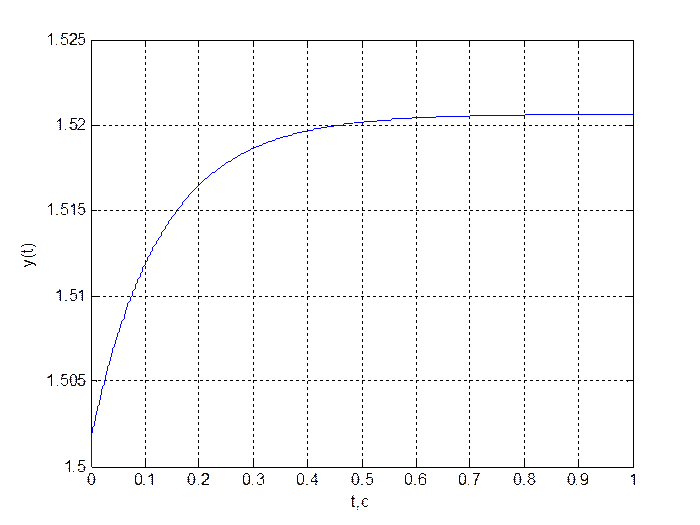
Рис. 7. График переходного процесса

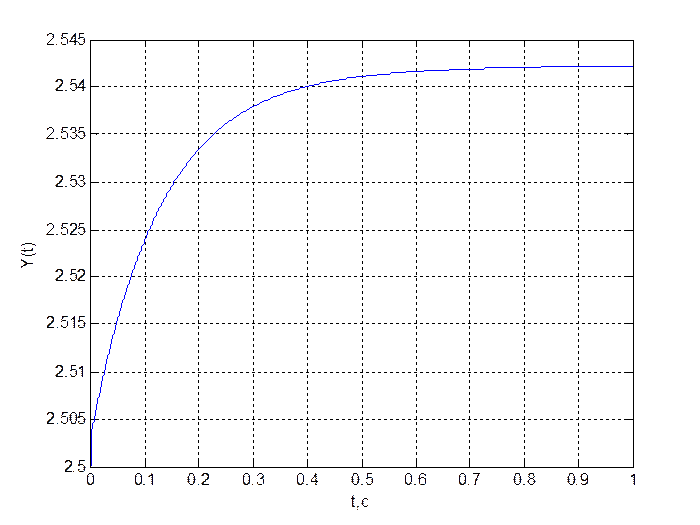
Рис. 8. График переходного процесса

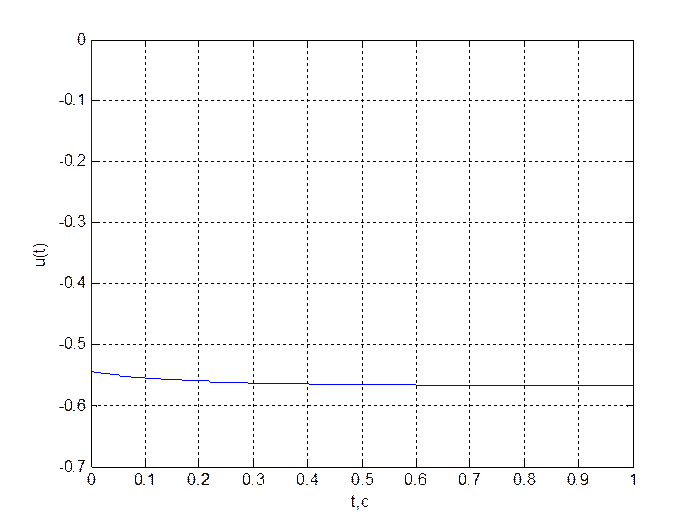
Рис. 9. График переходного процесса

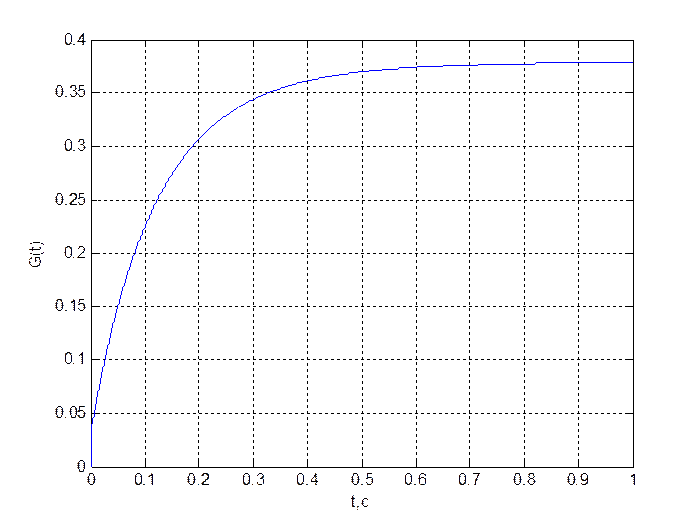
Рис. 10. График переходного процесса

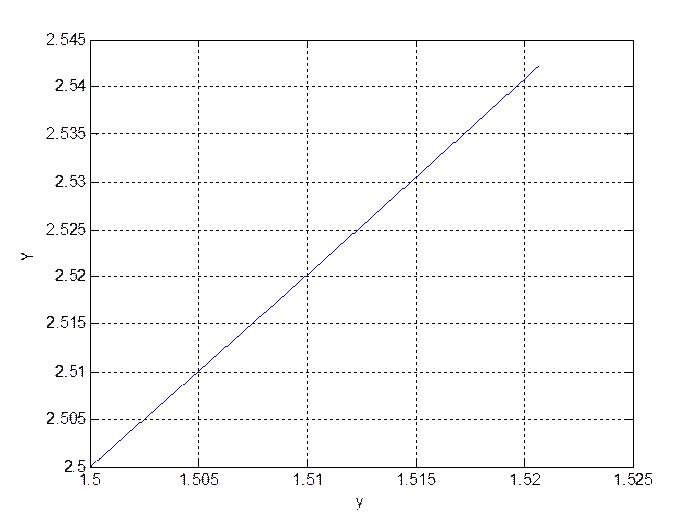
Рис. 11. Траектория движения системы на плоскости

Выводы

Для заданного объекта управления была рассчитана система экстремального регулирования, но т.к. объект неустойчив не удалось его стабилизировать. Исследовали объект с измененными параметрами. Время переходного процесса  и , что удовлетворяет заданным требованиям к качеству процесса выхода на экстремум.