Расчет устройства управления для системы из 3-х грузов на пружине

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра вычислительной техники

Дисциплина “Основы теории управления”

Расчетно-графическая работа

На тему:

Расчет устройства управления для системы из 3-х грузов на пружине

Группа:          АМ-110

Студент:        Каюров В.Н

Вариант:        9

Преподаватель:         Воевода А.А.

Новосибирск 2003

1.  Задание

Найти устройство управления для заданной системы такое, чтобы система была устойчивой

2.  Математическое описание системы

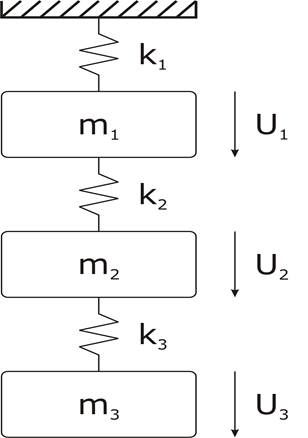
Индивидуальные данные:

m₁=m₂=m₃=1,  k₁=k₂=k₃=1

U₁=0

Регулировать выходы y₂,y₃

Уравнения Ньютона для системы:

После преобразования Лапласа получаем:

Выразим y1, y2 и y3:

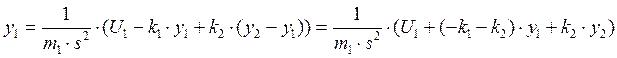
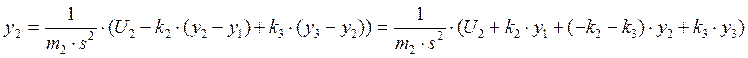
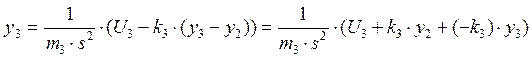
3. 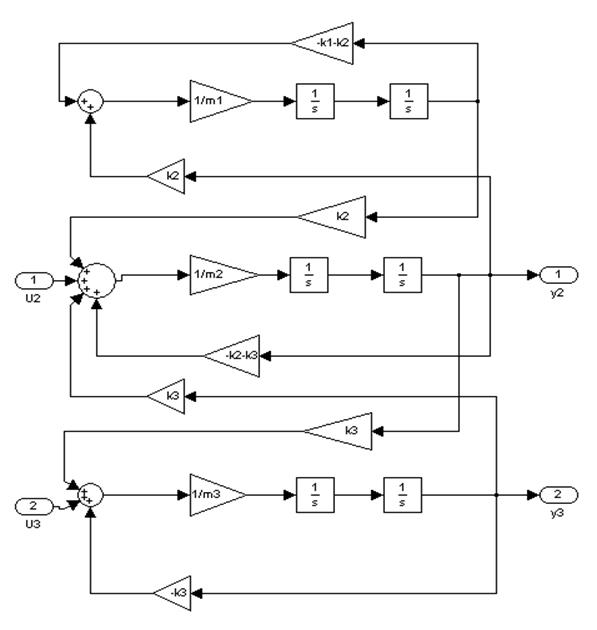 Структурная схема исходной системы

После упрощения, т.к. m_i=k_i=1 получаем:

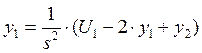
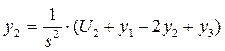
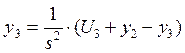
Структурная схема после упрощения, учитывая, что U₁ и y₁ нулевые

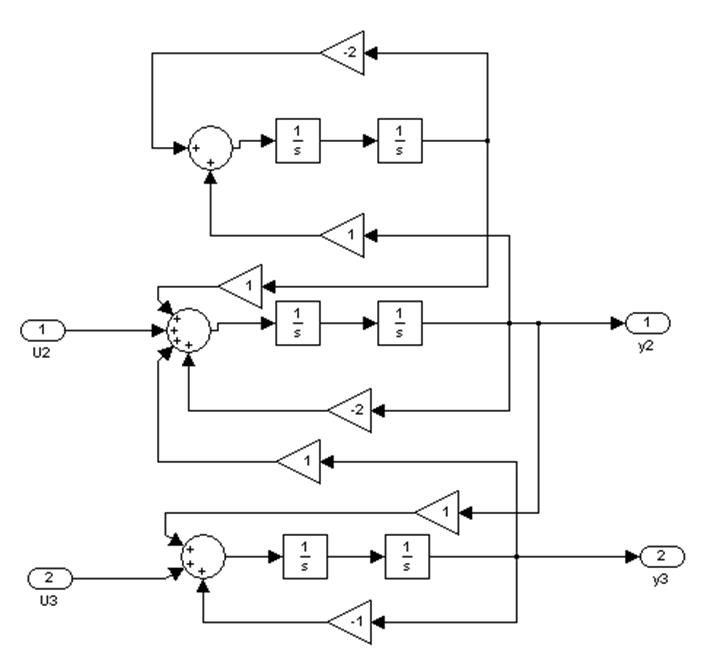
4.  Синтез устройства управления (УУ) алгебраическим методом

а) УУ для входа U₂ и выхода y₂

Для синтеза УУ положим U₃ и y₃ равными нулю.

Упрощенная схема объекта с регулятором

 

Структурная схема системы без регулятора

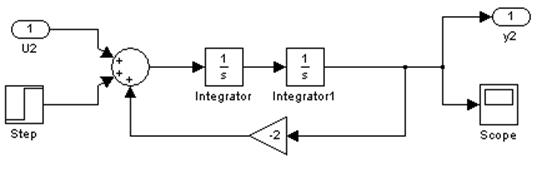
Переходные процессы в системе без регулятора

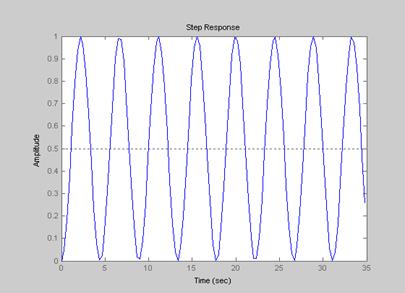
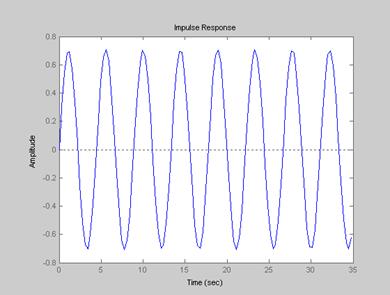
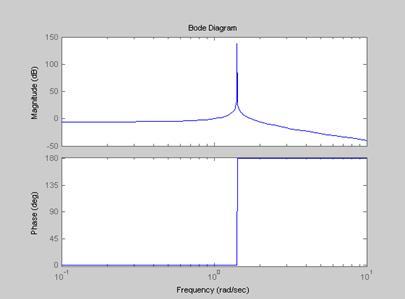
Расчет регулятора.

Для начала найдем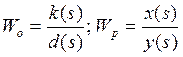           

 было найдено посредством MathLab с помощью данной программы:

[a,b,c,d] = linmod('u2y2');    //исходный файл схемы

sys=tf(ss(a,b,c,d))                 //трансфертная функция

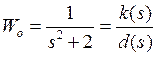
Степень регулятора на порядок ниже, поэтому получаем  в общем виде:

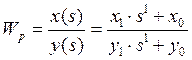
Для замкнутой системы получаем:

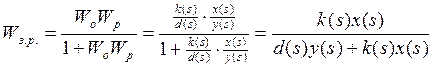
Х.П.З.С. системы с регулятором:

     

       

=

 

      

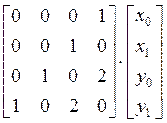Приравнивая коэффициенты при соответствующих степенях S, и, решая полученную

 систему уравнений, получим:

      

   

Подставим полученные значения:

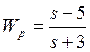
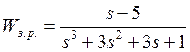
Схема с регулятором

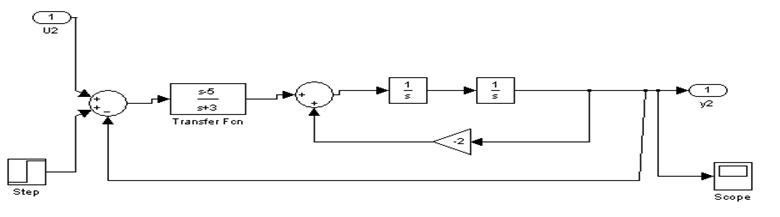
Переходные процессы с регулятором

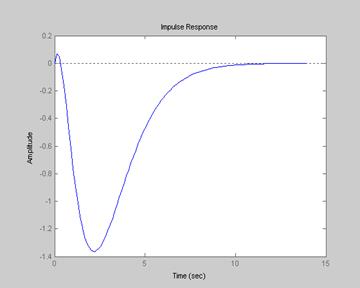
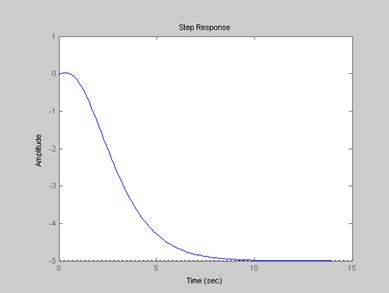
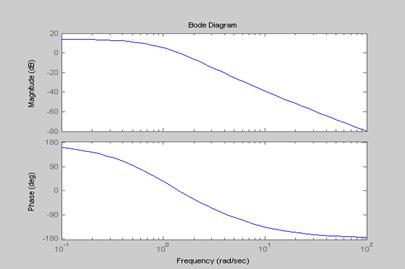
б) УУ для входа U₃ и выхода y₃

Для синтеза УУ положим U₂ и y₂ равными нулю.

Упрощенная схема объекта с регулятором

 

Структурная схема системы без регулятора

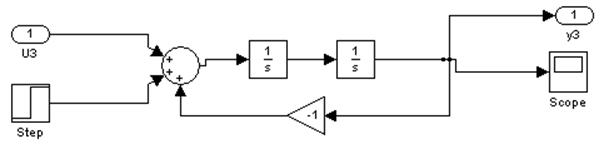
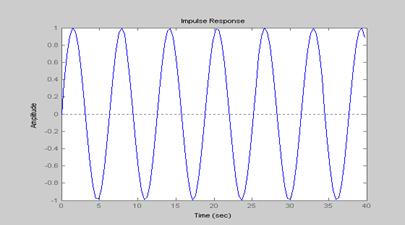
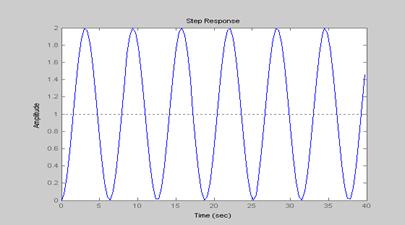Переходные процессы в системе без регулятора

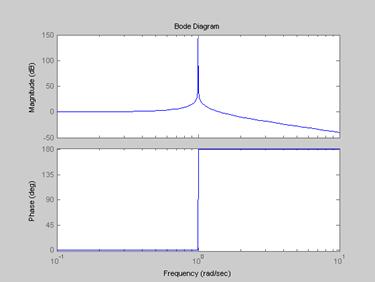
Расчет регулятора.

Для начала найдем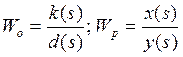           

 было найдено посредством MathLab с помощью данной программы:

[a,b,c,d] = linmod('u3y3');    //исходный файл схемы

sys=tf(ss(a,b,c,d))                 //трансфертная функция

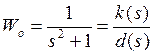
Степень регулятора на порядок ниже, поэтому получаем  в общем виде:

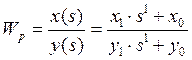
Для замкнутой системы получаем:

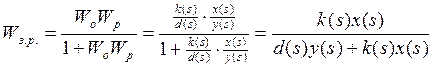
Х.П.З.С. системы с регулятором:

          

       

=

 

      

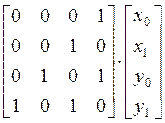Приравнивая коэффициенты при соответствующих степенях S, и, решая полученную

 систему уравнений, получим:

      

   

Подставим полученные значения:

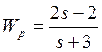
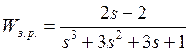
Схема с регулятором

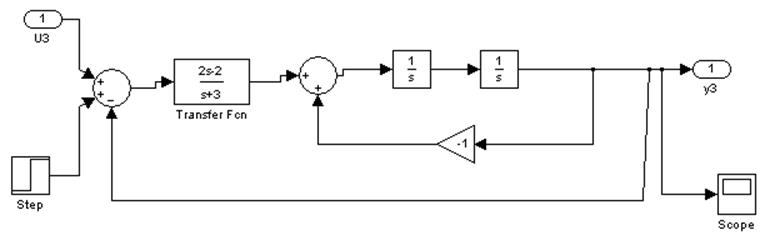
Переходные процессы с регулятором

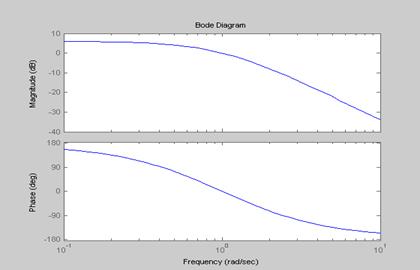
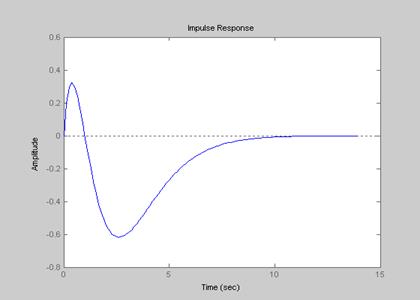
5.  Схема с двумя регуляторами

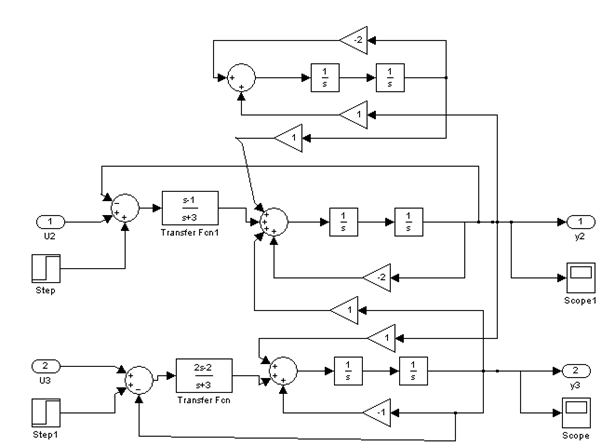
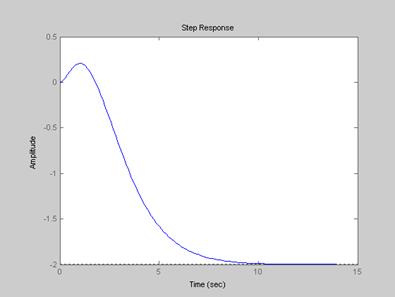
Переходные процессы с регуляторами

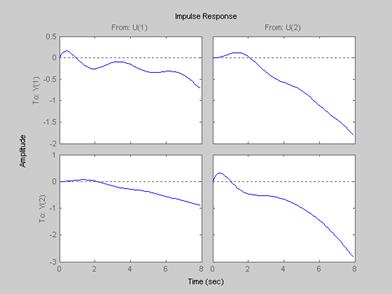
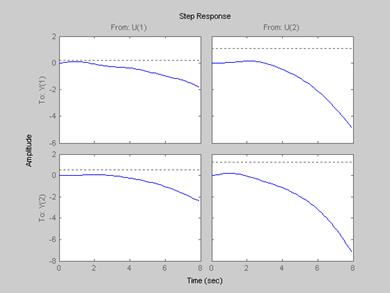
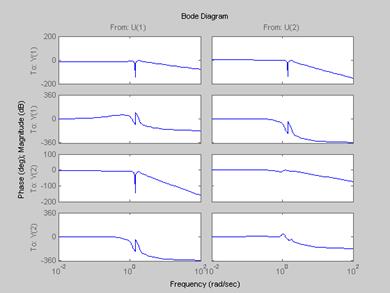
Как показывают графики, наша схема с регуляторами неустойчивая.

Теперь подберем регулятор U₂-y₂ для схемы с регуляторами U₂-y₂  и U₃-y₃.

Будем рассматривать схему, данную ниже, как объект и подберем для него регулятор

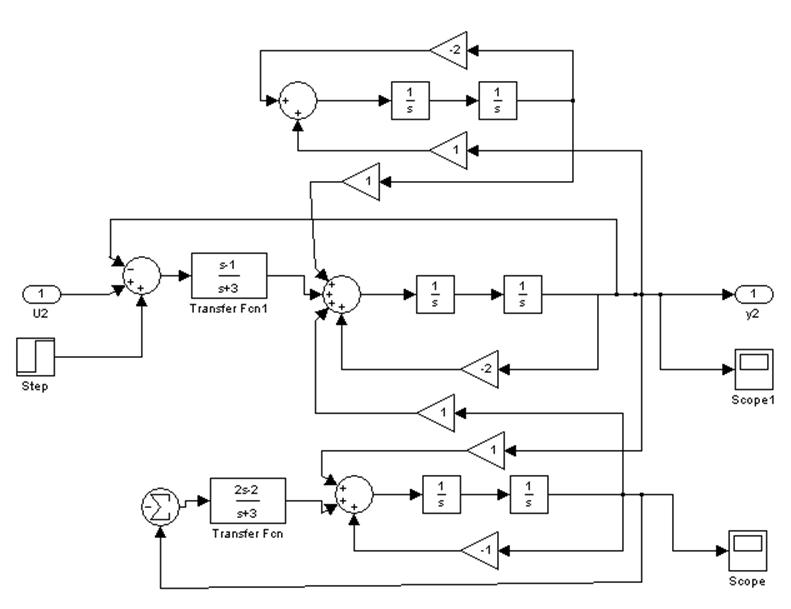
Для начала найдем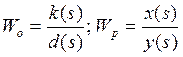           

 было найдено посредством MathLab с помощью данной программы:

[a,b,c,d] = linmod('u1y3');    //исходный файл схемы

sys=tf(ss(a,b,c,d))                 //трансфертная функция

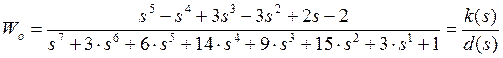
Степень регулятора на порядок ниже, поэтому получаем  в общем виде:

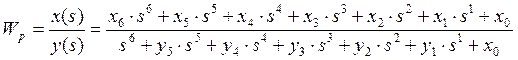
Для замкнутой системы получаем:

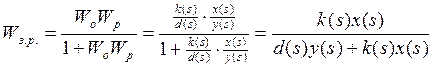
Х.П.З.С. системы с регулятором:

Произведем вычисления с помощью Excel в матричном виде: