Рассчет и исследование с помощью моделирования в среде MATLAB системы экстремального регулирования (с учетом необходимых оценок производных) для объекта с заданной математической моделью

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Новосибирский Государственный Технический Университет

Кафедра автоматики

Индивидуальное задание  №1 по курсу

Оптимальные и адаптивные системы

Вариант №10

Факультет: АВТ                                                              Преподаватель:

Группа: ААM-01                                                             Французова Г.А.

Студент:  Розенталь П.

Новосибирск, 2010

Цель работы

Рассчитать и исследовать с помощью моделирования в среде MATLAB систему экстремального регулирования (с учетом необходимых оценок производных) для объекта, математическая модель которого имеет вид:

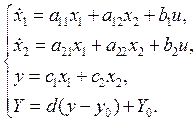
Известны ограничения на переменные состояния и управляющее воздействия: , , . Заданы требования к качеству процесса выхода на экстремум в виде следующих оценок:  и .

Численные значения параметров системы приведены в таблице 1.

Таблица 1

1	1	-1	-4	0	3	2	1	2	-1	-	25	60	500	1	0

Выполнение работы

Подставив в исходную систему численные значения из табл. 1, получим математическую модель объекта:

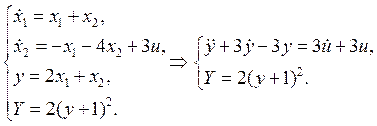                                    (1)

Для синтеза экстремальной системы будем рассчитывать регулятор основанный на методе локализации.

Относительный порядок объекта равен единице. Следовательно, согласно методу синтеза формируется управляющее воздействие

, где  – параметр регулятора, а  – желаемое уравнение, которое формируется исходя из заданных требований к системе. Так как в системе не допускается перерегулирование, корни должны быть вещественными и располагаться на расстоянии не ближе . Выбирается следующий возможный корень:

.

Формируется желаемое характеристическое уравнение:

.

Следовательно желаемое дифференциальное уравнение имеет вид:

.

На основании требования к статике

получим

,

                                                                        (2)

Выражение для градиента имеет вид:

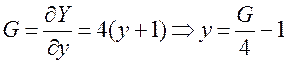.                                                 (3)

Подставляя (3) в (2) получим желаемое дифференциальное уравнение

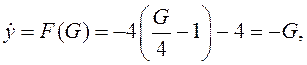
Определяется численное значение коэффициента усиления регулятора из соотношения . Т.к. , получим . Выберем .

Проверим ресурсное ограничение:

.

Найдём  и .

Из исходной системы (1) получим дифференциальное уравнение объекта виде:

.

.

В итоге получим:

.

Следовательно, в системе можно обеспечить желаемые процессы.

В законе управления используется не сама производная, а её оценка, которую получаем при помощи дифференцирующего фильтра, передаточная функция которого имеет вид:

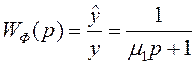, где – постоянная времени дифференцирующего фильтра.

Оценка градиента G осуществляется с помощью фильтра оценки частной производной, модель которого имеет вид:

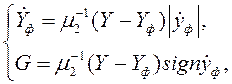
где – постоянная времени фильтра оценки частной производной.

С учётом условия разделимости движений выберем , .

Моделирование

Моделируемая система приведена на рис.1. Моделирование проводится при начальных условиях:

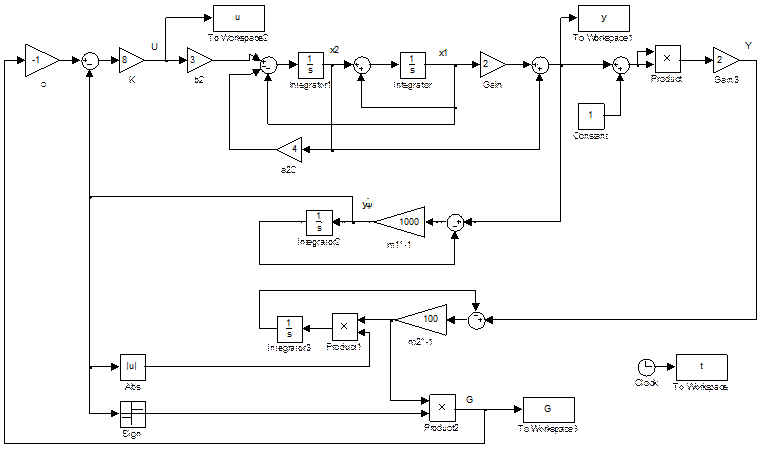
Рис.1. Моделируемая система

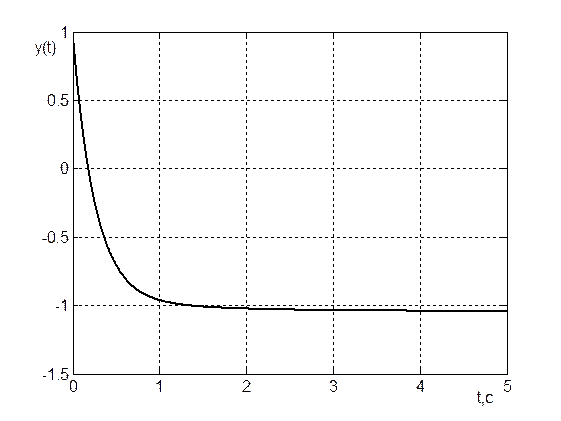
Рис.2. График переходного процесса y(t) при

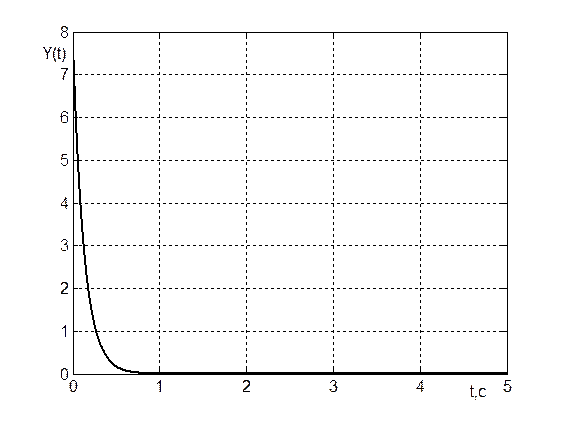
Рис.3. График переходного процесса Y(t) при

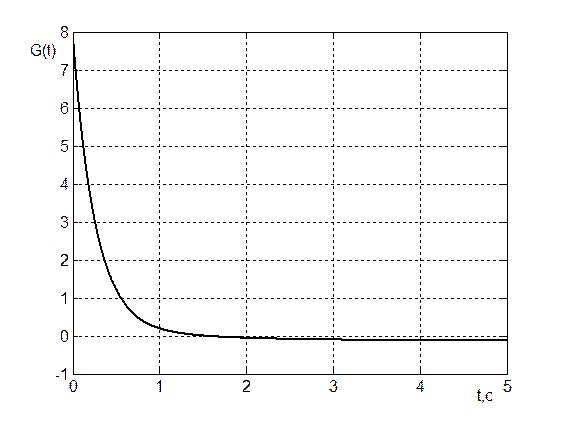
Рис.4. График переходного процесса G(t) при

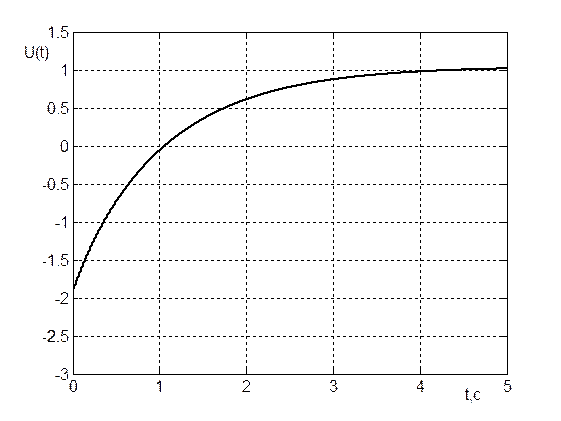
Рис.5. График переходного процесса U(t) при

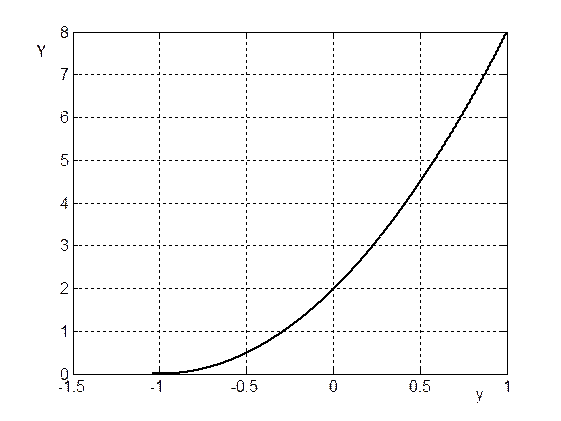
Рис.6. Портрет системы (y,Y) при

Выводы

В ходе расчётно-графической работы была рассчитана и исследована с помощью моделирования в среде MATLAB система экстремального регулирования.

Рассчитанная система удовлетворяет заданным требованиям к качеству процесса выхода на экстремум ( и .)

Статическая ошибка составляет менее пяти процентов (см. рис 2.). Ресурс управления не превышен (см. рис 5).