В условиях пассивного эксперимента организация работы по сбору данных связана с выбором средств регистрации параметров процесса. Обработка же результатов нацелена в конечном итоге на получение уравнения регрессии. Для достижения конечной цели при этом необходимо проводить расчет средних значений и дисперсий переменных; формирование целевой функции, с помощью которой при подборе коэффициентов уравнения регрессии можно обеспечить минимум расхождения результатов эксперимента с идентифицируемой математической моделью.
Для подбора коэффициентов, в MATLABe можно использовать процедуру-функцию минимизации функций нескольких переменных FMINS. Справку о ней можно получить с использованием команды help fmins.
Целевая функция F для k факторов формируется для конкретной задачи по условию:
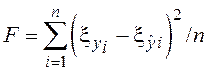 ,
,
где ![]() -
нормированные значения выходного показателя регистрируемого процесса y
-
нормированные значения выходного показателя регистрируемого процесса y
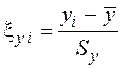 ;
;
![]() - средние значения выходного показателя
- средние значения выходного показателя
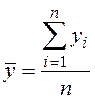 ;
;
![]() , -
среднеквадратичное отклонение (рассеяние) результатов выборки
, -
среднеквадратичное отклонение (рассеяние) результатов выборки
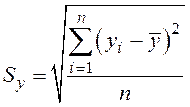 ;
;
![]() -
ординаты искомого линейного уравнения регрессии в точках, формирующих выборку в
виде
-
ординаты искомого линейного уравнения регрессии в точках, формирующих выборку в
виде
![]() ;
;
![]() - нормированные значения параметров исследуемого
процесса Tj (j=1 … k)
- нормированные значения параметров исследуемого
процесса Tj (j=1 … k)
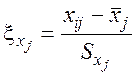 ;
;
![]() , -
среднеквадратичное отклонение (рассеяние) параметров в выборке
, -
среднеквадратичное отклонение (рассеяние) параметров в выборке
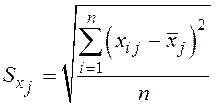 ;
;
![]() - средние значения j – го параметра
- средние значения j – го параметра
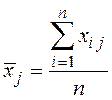 .
.
Таким образом, по сформированной целевой функции искомыми являются коэффициенты регрессии bj,. В качестве первого приближения любые вещественные числа.
Текст программы:
%Исходные значения коэффициентов регрессии
b1=1; b2=1;
%Данные эксперимента, взятые в обработку
% s2-число регистрируемых факторов
S2=3;
%Число фиксированных наблюдений, взятых в обработку
[n,s2]=size(q);
%Tемпература в помещении
T=q(1:n,1);
%Tемпература от окружающей среды
T1=q(1:n,2);
%Tемпература от социальной среды
T2=q(1:n,3);
%Средние значения переменных для выбранных данных
sumT1=0;
sumT2=0;
sumT=0;
for i=1:n
sumT1=sumT1+T1(i);
sumT2=sumT2+T2(i);
sumT=sumT+T(i);
end
Td1=sumT1/n;
Td2=sumT2/n;
Td=sumT/n;
______________________________________________________
%Выборочные рассеяния по данным измерений
sumT1=0;
sumT2=0;
sumT=0;
for i=1:n
sumT1=sumT1+(T1(i)-Td1)^2;
sumT2=sumT2+(T2(i)-Td2)^2;
sumT=sumT+(T(i)-Td)^2;
end
STd1=sqrt(sumT1/n);
STd2=sqrt(sumT2/n);
STd= sqrt(sumT/n);
%Безразмерные переменные, полученные по температурам
%от социальной и внешней сред
dz1=(T1-Td1)/STd1;
dz2=(T2-Td2)/STd2;
%Безразмерное отклонение от среднего значения в %помещении по данным измерений
dt=(T-Td)/STd;
%Среднее значение температуры в помещении по уравнению %регрессии
sumT=0;
y=b1*T1+b2*T2;
for i=1:n
sumy=sumy+y(i);
end
ysr=sumy/n;
%Величины безразмерного отклонения температуры по
%уравнению регрессии
dzet=T1*b1+T2*b2;
%Выборочная дисперсия данных по уравнению регрессии
%и результатами измерений, соответствующая конечной %форме целевой фунции
sumy=0;
for i=1:n
sumy=sumy+(dz(i)-dzet(i))^2;
end
F=sqrt(sumy/n);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.