Относительно простая справа (relatively right prime) пара полиномиальных матриц

1.  ВВЕДЕНИЕ

Любая невырожденная полиномиальная матрица P(s) столбцово (строчно) эквивалентна столбцово (строчно) правильной матрице. Т.е. может быть всегда найдена унимодальная матрица U_R(S) (U_L(s)), которая приводит P(s) к столбцово (строчно) правильной форме.

Пример. Для матрицы

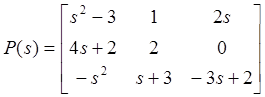
степени столбцов равны соответственно  _с1 = 2, _{с 2} = 1, _{с 3} = 1 и степени строк равны _{r 1} = 2, _{r 2} = 1, _{r 3} = 2; матрицы коэффициентов при старших столбцовых степенях Г_с и при старших строчных степенях Г_r  равны соответственно

,  .

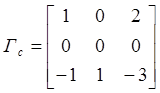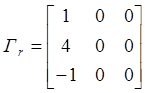Матрица P(s) не является столбцово приведенной, так как |Г_с| = = 0. Кстати, найдем определитель матрицы P(s):

|P(s)| = 6s³ + 44s² + 28s – 16 ≠ 0.

Отметим, что степень его меньше суммы степеней как строк, так и столбцов. Введем матрицу P^c(s)  Г_с· diag[]:

.

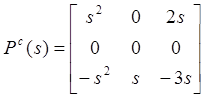Из |Г_с| = 0 и определения P^c(s) следует, что матрица вырожденная,

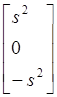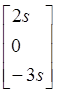-2 + s + s = 0.

Следовательно, если сложить столбцы с коэффициентами 1, -s/2, -s/2, то первый столбец матрицы P^c(s) исчезнет. Это можно выполнить при помощи умножения матрицы P(s) справа на U₁(s):

  P(s)U₁(s)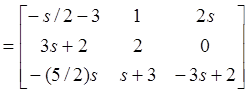 

Эта матрица столбцов правильная:

■

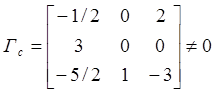Теорема. Рассмотрим пару {P(s), R(s)} ({P(s),Q(s)}) полиномиальных матриц, которые имеют одно и то же число столбцов (строк). Если составная/блочная (composite) матрица

, ()

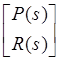сводится к верхнетреугольной (нижнетреугольной) форме

, (),

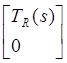тогда T_R(s) (T_L(s)) есть наибольший общий правый делитель G_R(s) пары {P(s), R(s)} (наибольший общий левый делитель G_L(s) пары {P(s), Q(s)}).

Определение. Пара полиномиальных матриц {P(s), R(s)} ({P(s), Q(s)}), имеющих одно и то же число столбцов (строк), называется относительно простой справа (relatively right prime) (слева), если их наибольший общий правый делитель (наибольший общий левый делитель) – унимодальная матрица.