






11. ПРИВЕДЕНИЕ СКАЛЯРНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ К ВЗАИМО ПРОМТОМУ ВИДУ
Пусть ![]() некоторая передаточная функция, которую
запишем в виде
некоторая передаточная функция, которую
запишем в виде
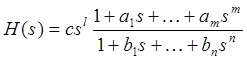 , (1)
, (1)
где ![]() и
и ![]() комплексные константы с
комплексные константы с ![]() ,
, ![]() и
и ![]() - неотрицательные целые,
- неотрицательные целые, ![]() некоторое целое. Задача состоит в
определении коэффициентов
некоторое целое. Задача состоит в
определении коэффициентов ![]() , таких, что
, таких, что
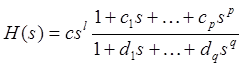 , (2)
, (2)
где ![]() и
и ![]() взаимно простые. Алгоритм включает в себя
пять шагов.
взаимно простые. Алгоритм включает в себя
пять шагов.
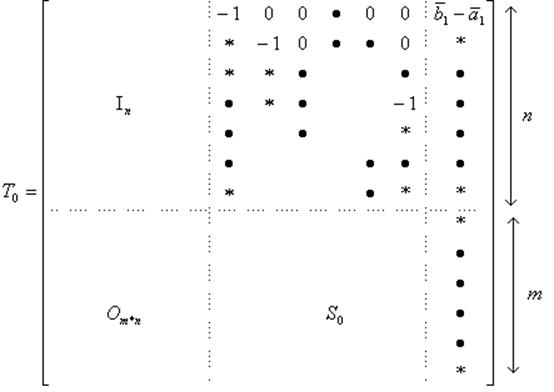
Шаг 1. Предположим, что ![]() . Тогда мы запишем так называемую би-теплицеву
матрицу (bi-Toeplitz matrix)
. Тогда мы запишем так называемую би-теплицеву
матрицу (bi-Toeplitz matrix) ![]() размерами
размерами ![]() следующим образом:
следующим образом:
![]()
![]()
![]()

![]()
![]()
![]()
Если ![]() ,
достаточно перейти к рассмотрению обратной передаточной функции, т.е. поменять
местами
,
достаточно перейти к рассмотрению обратной передаточной функции, т.е. поменять
местами ![]() и
и ![]() . Таким
образом, мы всегда сформируем матрицу
. Таким
образом, мы всегда сформируем матрицу ![]() такую,
что ширина блока
такую,
что ширина блока ![]() будет меньше ширины блока
будет меньше ширины блока ![]() .
.
 |
![]()
![]()
![]()
где ![]() единичная
матрица размером
единичная
матрица размером ![]() (единичный блок),
(единичный блок), ![]() нулевой блок размером
нулевой блок размером ![]() , и
, и ![]() блок.
Так как
блок.
Так как ![]() теплицева матрица и все ведущие элементы
равны единице (элемент на диагонали блока
теплицева матрица и все ведущие элементы
равны единице (элемент на диагонали блока ![]() матрицы
матрицы
![]() ), эта процедура не вызывает затруднений.
), эта процедура не вызывает затруднений.
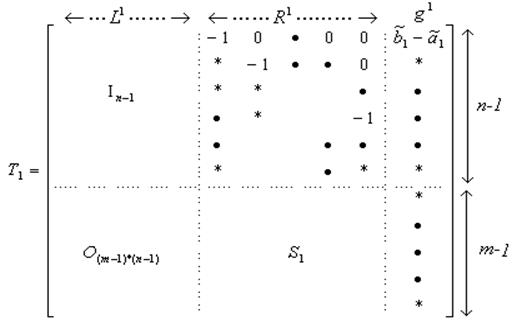 |
Шаг 4. Проверим ранг ![]() .
Если
.
Если ![]() имеет полный ранг, тогда продолжим строчные
операции над
имеет полный ранг, тогда продолжим строчные
операции над ![]() с целью получения
с целью получения
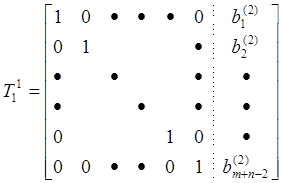
![]()
и заключаем, что
![]() ,
, ![]()
![]()
Если ![]() неполного ранга, тогда удаляем последний
столбец
неполного ранга, тогда удаляем последний
столбец ![]() , последний столбец
, последний столбец ![]() и
две последние строки
и
две последние строки ![]() , получая
, получая
![]()
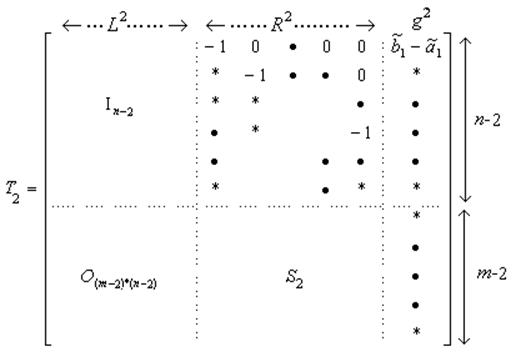 |
где ![]() блок.
блок.
Шаг 5. Повторим процедуру шага 4 k-раз, до тех пор, пока не получим
матрицу ![]() размерами
размерами ![]()

![]()
Окончательный результат следующий:
![]() ,
, ![]() ,
,
![]() ■
■
Пример. Рассмотрим заданную передаточную функцию
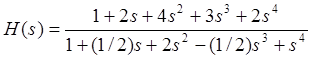 , где
, где ![]() .
Положим
.
Положим
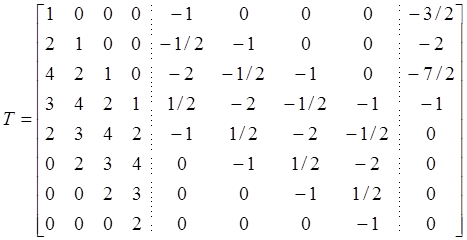 .
.
Используя строчные операции для
упрощения матрицы ![]() , получим
, получим
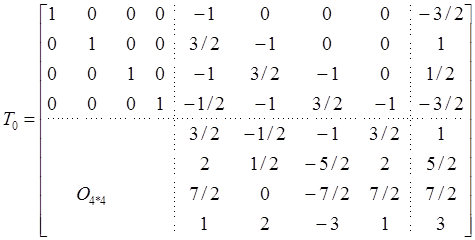
![]()
![]()
![]()
Так как матрица ![]() сингулярная (сумма трех столбцов равна
нулю), удаляем четвертый и восьмой столбцы и две последние строки
сингулярная (сумма трех столбцов равна
нулю), удаляем четвертый и восьмой столбцы и две последние строки ![]() и получаем
и получаем
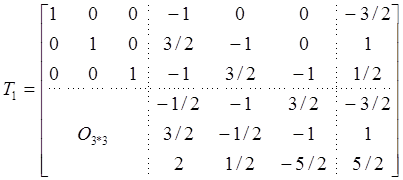
![]()
![]()
![]()
Легко увидеть, что матрица ![]() сингулярная, и таким образом мы должны
удалить третий и шестой столбцы и две последние строки
сингулярная, и таким образом мы должны
удалить третий и шестой столбцы и две последние строки ![]() ,
получив
,
получив
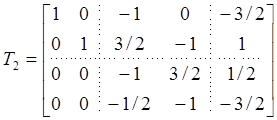 .
.
Но сейчас матрица ![]() имеет полный ранг, и таким образом мы,
продолжив строчные операции над
имеет полный ранг, и таким образом мы,
продолжив строчные операции над ![]() , получим
, получим
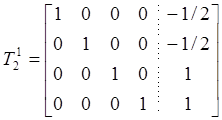 .
.
Возможная последовательность преобразований:
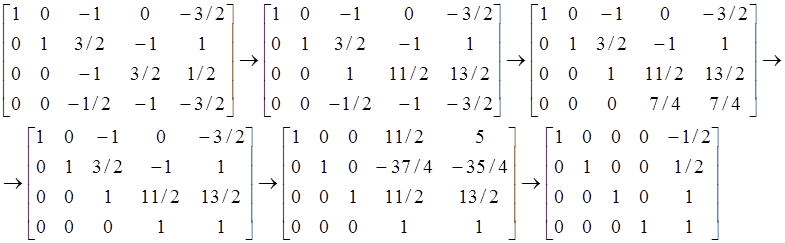
Окончательный результат следующий:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
и
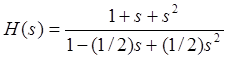 ■
■
Обоснование
алгоритма. Пусть
![]() будет соответствовать приведенной (сокращенной)
форме
будет соответствовать приведенной (сокращенной)
форме ![]() , заданной (1), где
, заданной (1), где
![]() ,
, ![]() .
.
Тогда имеем ![]() и
и
![]() или эквивалентно
или эквивалентно
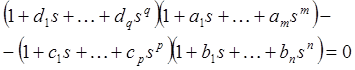
Перемножая левую часть приведенного выше равенства и приравнивая
коэффициенты при равных степенях ![]() , где
, где ![]() ,
, ![]() ,
получим в случае
,
получим в случае ![]()
![]()
![]()
. . . . .
![]()
. . . . .
![]()
![]()
![]()
. . . . .
![]()
![]()
. . . . .
![]()
![]() .
.
Эта система уравнений имеет следующую матричную форму:
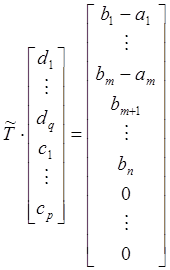 .
.
Где ![]() задается
задается
![]()
![]()
 ,
,
![]()
![]()
которая получена из ![]() удалением последних
удалением последних ![]() столбцов из
столбцов из ![]() ,
последних
,
последних ![]() столбцов из
столбцов из ![]() (где
(где ![]() ) и последних
) и последних ![]() строк
строк ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.