Стабилизация двухмассовой системы: модальный метод синтеза

СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2009. – № 2(56). – 3–10

автоматическое управление и идентификация

УДК 681.513

СТАБИЛИЗАЦИЯ ДВУХМАССОВОЙ СИСТЕМЫ: МОДАЛЬНЫЙ МЕТОД СИНТЕЗА

А.А. Воевода^©, Е.А. Ижицкая§,

Сформулирована технология синтеза системы АУ модальным методом на примере объекта, представляющего два консервативных звена, и регулятор полного порядка. Подразумевается, что регулятор рассчитывается на основе использования диофантова уравнения. Приведенная технология может быть использована в качестве шаблона для синтеза систем с произвольным объектом модальным методом.

Пусть рассматривается объект управления в общем виде

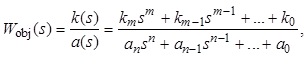
где m<n.

Число коэффициентом соответственно m + 1 и n + 1. Такое описание избыточно, поэтому коэффициент при старшей степени полинома знаменателя a_n+1 можно сделать равным единице, разделив на него все коэффициенты.

Пусть передаточная функция регулятора имеет вид

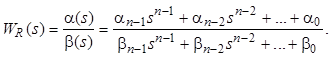
Степень каждого полинома n–1, количество коэффициентов – 2n. Описание и здесь избыточное, поэтому коэффициент β_n–1 при степени n–1 полинома знаменателя также можно привести к 1.

Передаточная функция замкнутой системы

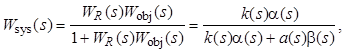
т. е. характеристический полином замкнутой системы

будет иметь степень 2n–1 и 2n коэффициентов. Здесь , где , как следствие из равенств a_n=1  и β_n–1=1. Коэффициенты желаемого полинома

Приравнивая коэффициенты действительного и желаемого уравнений, получаем систему

где A включает коэффициенты объекта; x – искомые коэффициенты регулятора, b – коэффициенты желаемого характеристического полинома. Рассмотрим метод на примере.

Пусть рассматривается объект 5-го порядка

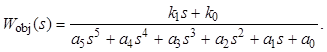
Синтезируем систему АУ с регулятором полного порядка для этого объекта

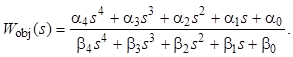
Характеристический полином замкнутой системы (ХПЗС)

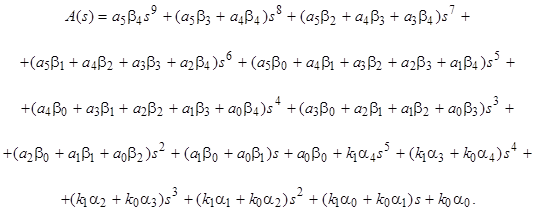
Пусть все полюсы желаемого ХПЗС будут равны единице

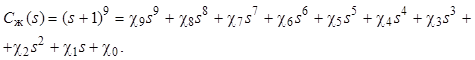
Для удобства вычисления ХПЗС можно представить в матричном виде

.

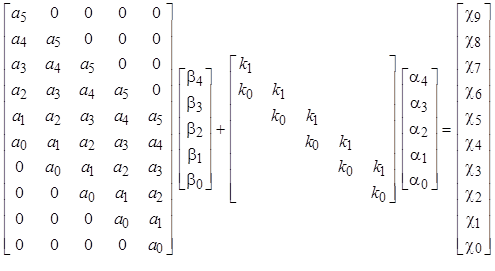Представим матрицы в следующем виде:

.

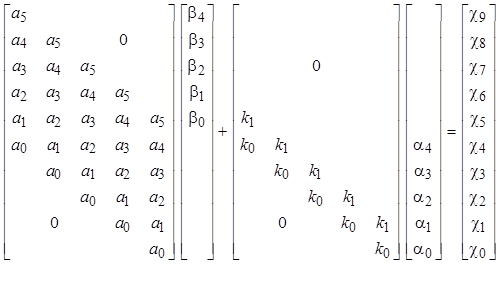Рассмотрим частный случай

           

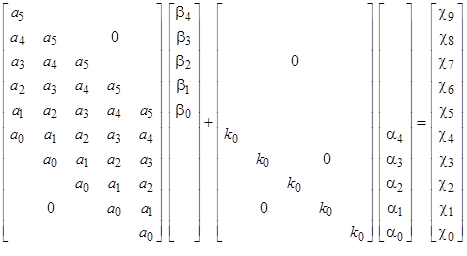
Объединим вышеприведенные матрицы в одну на основе следующих соображений:

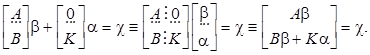
Объединив матрицы коэффициентов, получим

.

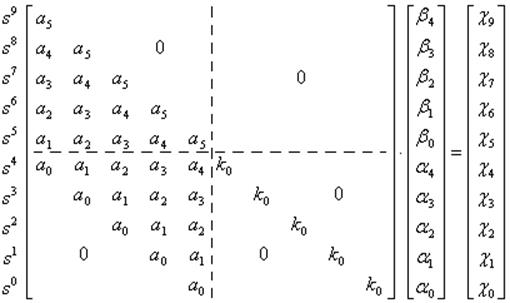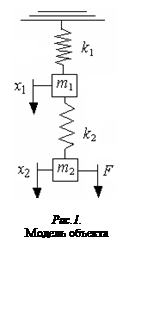Рассмотрим синтез для объекта, представляющего собой два консервативных звена.

Модель объекта представляет собой систему из двух грузов разной массой m₁ и m₂, подвешенных последовательно на двух пружинах разной жесткости k₁ и k₂, Управляющее воздействие F приложено ко вторму грузу, измеряемая переменная – x₁.

Координаты x₁ и x₂ отсчитываются от состояния равновесия.

Уравнение первого звена

Уравнение второго звена

Сведем к одному уравнению

Дважды дифференцируя, подставим в уравнение выражение   

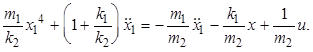
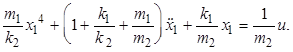
В операторной форме данное уравнение принимает вид

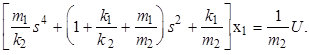
Передаточная функция объекта

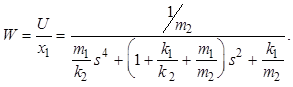
Домножая на k₂, получаем передаточную функцию объекта

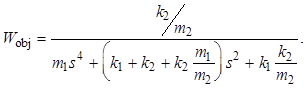
Для простоты подберем коэффициенты системы так, чтобы получить объект

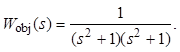
Потребуем астатизма системы, для чего введем интегратор, который отнесем к объекту. Таким образом,

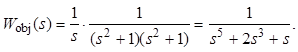
Для приведенного объекта:

Поскольку  то первая строка матрицы коэффициентов объекта, умноженная на первую строку матрицы коэффициентов регулятора, всегда даст единицу в матрице коэффициентов желаемого уравнения системы, следовательно, это уравнение не влияет на дальнейшие расчеты и первую строку каждой матрицы можно исключить из дальнейшего анализа:

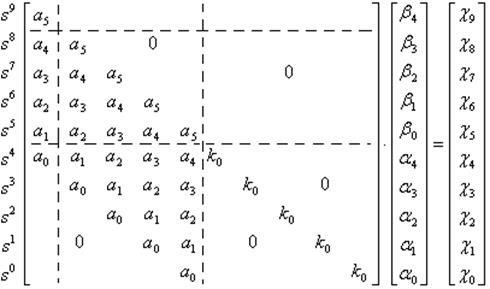
Запишем эту матрицу без первой строки, которая не влияет на вычисления, и отнимем первый столбец матрицы коэффициентов объекта от матрицы коэффициентов желаемого ХПЗС:

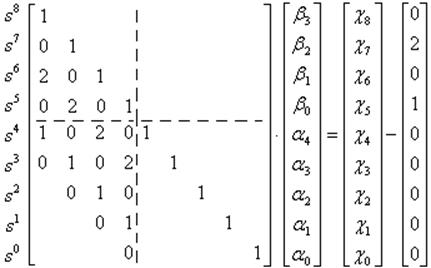
Обозначим матрицы следующим образом: матрица коэффициентов слева – A, матрица коэффициентов желаемого ХПЗС – В, матрица вычитаемых коэффициентов – С, матрица искомых коэффициентов регулятора – X. Тогда:Искомое решение

Запишем передаточную функцию регулятора с полученными коэффициентами

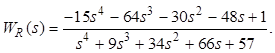
Проверка показывает, что передаточная функция замкнутой системы

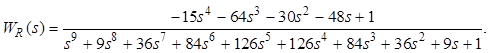
Таким образом, знаменатель передаточной функции замкнутой системы совпадает с заданным желаемым уравнением.

Переходный процесс в системе показан на рисунке светлой линией.

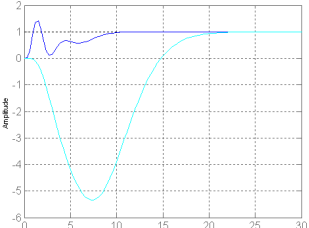
Time, s

Переходные процессы, полученные для замкнутой системы  с желаемыми полюсами: 1 – светлая линия и 2 – темная линия

Такой вид переходного процесса связан со сложностью объекта, для которого синтезируется регулятор, и с требуемым расположением корней. Зададим желаемый характеристический полином замкнутой системы

                                                      

Переходный процесс в системе показан на рисунке темной линией.

В заключение следует отметить, что задание желаемых полюсов замкнутой системы в общем случае не позволяет получить требуемые качества переходного процесса. Кроме того, в передаточной функции замкнутой системы объединены нули объекта и регулятора, которые могут существенно влиять на вид переходного процесса. Это подсказка для задания всех полюсов или их части либо части нулей системы.

При вычислении коэффициентов регулятора в  MatLab удобно использовать операторное выражение: X=inv(A)(B–C).