Исследование инверсного ферромагнитного преобразователя частоты

УДК 621.316.176

Исследование инверсного ферромагнитного преобразователя частоты

Воробей А. М.

Научный руководитель СОНЧИК Л. И., кандидат технических наук, доцент

Особый теоретический и практический интерес представляет возможность работы ферромагнитных преобразователей частоты в инверсном режиме. Обязательным элементом инверсного преобразователя частоты является колебательный контур, включающий в себя нелинейный элемент [1].

Подтверждением работоспособности инверсных преобразователей частоты служат и некоторые экспериментальные исследования [2]. Такие преобразователи могут служить в качестве связующего звена между системами промышленной и утроенной частоты.

Практическое применение преобразователей частоты, наряду с вопросами анализа и расчета, связано с разработкой методов оптимизации их параметров. Оптимальное конструирование преобразователей частоты, как и других устройств с нелинейными элементами, предполагает выбор критерия оптимальности. В качестве критерия оптимальности инверсного преобразователя следует выбирать наиболее эффективный, определяющий его конкурентоспособность в сравнении с устройствами одинакового функционального назначения. Для силовых преобразователей параметров электроэнергии главным условием оптимального проектирования принято считать обеспечение минимального веса, объема или стоимости активных материалов на единицу установленной мощности при заданном допустимом перегреве [3,4]. Обеспечение минимальных весогабаритных показателей преобразовательных устройств невозможно без максимального использования материала его основного элемента – магнитопровода. Кроме этого для преобразователей частоты в инверсном режиме является обязательным наличие источников реактивной мощности, как на входе, так и на выходе устройства. При этом необходимо учесть, что вход и выход инверсного преобразователя являются понятиями относительными, зависящими от режима работы устройства – умножения или деления частоты. Поэтому оптимизация параметров инверсного преобразователя также невозможна без определения оптимальной величины емкостной компенсации.

Ранее рассматривались вопросы определения оптимальной емкостной компенсации в различных аспектах [5]. Величина оптимальной емкостной компенсации на выходе утроителей может быть определена из условия максимально отдаваемой мощности при исключении автоколебаний и триггерного эффекта или из условия обеспечения максимальной величины отношения суммарной намагничивающей силы трансформатора к суммарной намагничивающей силе умножителя [6]. Другие авторы [7] вопрос оптимальной емкостной компенсации рассматривают в связи с условием получения необходимой внешней характеристики утроителя. Вследствие выполнения разработанных нами устройств на базе магнитопровода заданной формы и габаритных размеров и обязательного наличия в них источников реактивной мощности выбираем в качестве критерия оптимальности отношение суммарной реактивной компенсирующей мощности к величине максимально отдаваемой активной мощности:

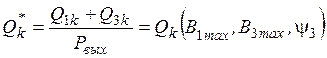,                             (1)

где  - относительная реактивная компенсирующая мощность;  – реактивная компенсирующая мощность со стороны первой и третьей гармоники соответственно.

Математически поставленная задача сводится у минимизации целевой функции относительной компенсирующей мощности при фиксированном значении амплитуды индукции основной гармоники:

,                               (2)

где  - значения амплитуды индукции третьей гармоники и ее начальной фазы, соответствующие оптимальному режиму.

Нахождение минимума относительной компенсирующей мощности инверсного преобразователя частоты ставит вопрос выбора аппроксимации характеристик линейных элементов устройства. Использование для данной задачи принятой в работе основной аппроксимации кривой намагничивания в форме выражения гиперболического синуса не позволяет получить решение в аналитическом виде. В связи с этим возникает необходимость замены основной аппроксимации эквивалентной ей в смысле идентичного отображения свойств сердечника устройства относительно преобразования энергии в инверсном режиме работы. Учитывая особенности режима работы преобразователя частоты, примем в качестве эквивалентной аппроксимации выражение степенного полинома. При этом с целью получения решения задачи в аналитическом виде степень полинома не должна быть выше третьей. В качестве критерия эквивалентности двух выражений аппроксимации кривой намагничивания сердечника примем равенство гармонического спектра напряженности поля. Для оценки эффективности изложенного метода выполним расчет характеристики холостого хода преобразователя в режиме умножения частоты при аппроксимации кривой намагничивания сердечника с помощью основной и эквивалентной аппроксимации.

Запишем выражение эквивалентной аппроксимации в действительных единицах: