Исследование инверсного ферромагнитного преобразователя частоты, страница 2

                                                                                    (3)

Коэффициенты аппроксимации степенного полинома определим из условия эквивалентности гармонического спектра напряженности поля. Для упрощения расчетов эквивалентирование двух выражений аппроксимации выполним при синусоидальной индукции. Приравнивая коэффициенты при членах с одинаковой частотой в выражениях разложения в ряд Фурье напряженности поля при использовании основной и эквивалентной аппроксимации, получим:

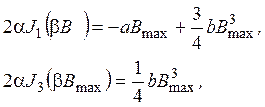                                                         (4)

где , - модифицированная функция Бесселя первого и третьего порядка соответственно.

Из полученной системы уравнений можно определить коэффициенты аппроксимации степенного полинома:

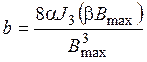                   ,                                                            (5)

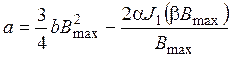                 .                                             (6)

Значение индукции первой гармоники в выражении эквивалентной аппроксимации определим из соотношения:

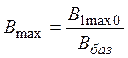                       ,                                                             (7)

где - значение индукции первой гармоники в выражении основной аппроксимации.

Значение базисной индукции определим из выражения:

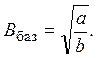                                                                              (8)

С учетом полученных соотношений можно записать выражение эквивалентной аппроксимации в относительных единицах:

                                                                          (9)

Принимаем закон изменения индукции в сердечнике преобразователя в виде:

                                        (10)

Подставив уравнение (10) в (9) выделим из кривой напряженности поля третью гармонику:

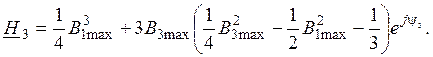                      (11)

В режиме холостого хода преобразователя:

                                                                                    (12)

Отсюда получим:

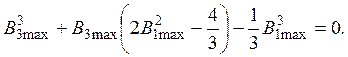                            (13)

Из уравнения (13) можно легко определить эквивалентное значение амплитуды индукции третьей гармоники. Обратный переход к величинам, соответствующим выражению основной аппроксимации, можно осуществить с помощью базисных единиц.

При использовании эквивалентной аппроксимации кривой намагничивания полная выходная и входная мощность преобразователя в относительных единицах может быть определена из выражения:

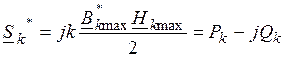            ,                                       (14)

где  – номер гармоники;  - реактивная компенсирующая мощность –той гармоники.

Активную и реактивную компенсирующую мощность первой и третьей гармоники определим из следующих выражений:

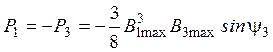            ,                                         (15) 

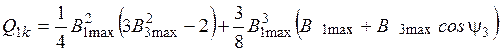            ,        (16)

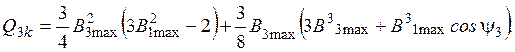                  (17)

Из приведенных уравнений следует, что при неизменной величине индукции основной гармоники максимально преобразуемой мощности соответствует угол 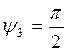, а минимальной компенсирующей мощности - .

В соответствии с методом наискорейшего спуска отыскание минимума критерия оптимальности будем выполнять, начиная с определения оптимального значения индукции третьей гармоники по выражению:

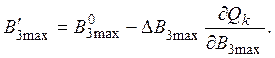                                          (18)

Начальное значение амплитуды индукции третьей гармоники определим из режима холостого хода устройства по уравнению (13).

Величина шага в уравнении (18) определяется из выражения:

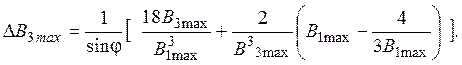      (19)

Величина оптимального угла  в уравнении (19) определяется начальной фазой амплитуды индукции третьей гармоники:

                                                                               (20)

где

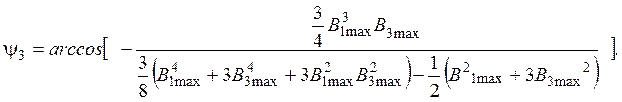
Обратный переход от полученных результатов к размерности, соответствующей основной аппроксимации, можно выполнить с помощью базисных величин:

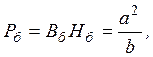                                                                              (21)

                                                                                                (22)

где  - базисная мощность; - базисная проводимость.

Литература

1.  Каримов А. С., Турдыев М. Г. Особенности возбуждения субгармонических колебаний в многоконтурных феррорезонансных целях переменного тока. – Электричество, 1979.

2.  Ешелькин В. М, Бурыкин В. В. Передача активной мощности в системе ферромагнитный преобразователь частоты – синхронная машина. – Известия высших учебных заведений. Серия Энергетика, 1981.

3.  Бертинов А. И., Кофман Д. Б. Тороидальные трансформаторы статических преобразователей. – М.: Энергия, 1970.

4.  Бальян Р. Х. Трансформаторы для радиоэлектроники. – М.: Радио, 1971.

5.  Обрусник В. П. Дискретно-управляемые ферромагнитные элементы для преобразования параметров электроэнергии. – М.: Наука,1979.

6.  Бамдас А. М., Блинов И. В., Захаров Н. В., Шапиро С. В. Ферромагнитные умножители частоты. – М.: Энергия, 1968.

7.  Баженов И. А. Исследование регулируемости статических ферромагнитных нечетнократных умножителей частоты. Автореф. дисс. канд. техн. наук. – Минск, 1971.