образования Республики Беларусь
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра “Электротехника и электроника”
Лабораторная работа по ТОЭ №30Н
ИССЛЕДОВАНИЕ электрического поля горизонтального цилиндрического заземлителя
М и н с к 2 0 10
Л а б о р а т о р н а я р а б о т а №30H
ИССЛЕДОВАНИЕ электрического поля горизонтального цилиндрического заземлителя
30.1. Цель работы
1. Исследование электрического поля вертикального цилиндрического заземлителя методом математического моделирования на ЭВМ.
2. Изучение методов расчета параметров электрического поля вертикального цилиндрического заземлителя в произвольной точке пространства.
3. Исследование влияния геометрических размеров вертикального цилиндрического заземлителя на его электрическое сопротивление.
30.2. Исходные данные
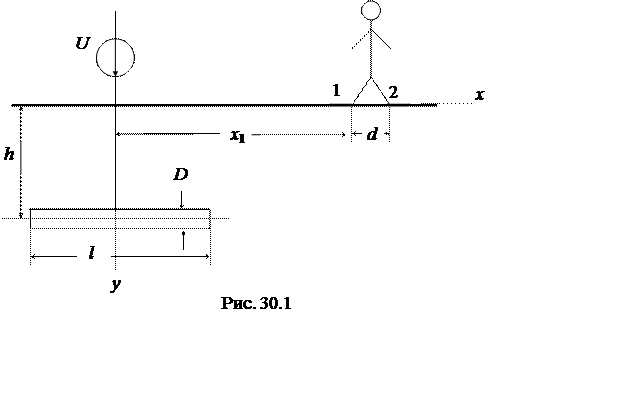
Заземлитель цилиндрической формы диаметром D погружен на глубину h в проводящую среду (землю) с заданной удельной проводимостью g (рис.30.1). К заземлителю приложено постоянное напряжение U. К заземлителю приближается человек, который находится на расстоянии x1 от его центра. Заданы координаты расчетной точки n(xn , yn). Исходные данные повариантно приведены в табл. 30.1.
 |
Т а б л и ц а 30.1
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
U, кВ |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
7,0 |
7,5 |
|
l, м |
2 |
2,5 |
3 |
3,5 |
4 |
2 |
2,5 |
3 |
3,5 |
4 |
|
h, м |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
|
D, см |
4 |
6 |
8 |
10 |
12 |
5 |
7 |
9 |
11 |
13 |
|
g,См/м |
0,01 |
0,02 |
0,03 |
0,01 |
0,02 |
0,03 |
0,01 |
0,02 |
0,03 |
0,01 |
|
xn, м |
4 |
5 |
6 |
7 |
8 |
9 |
4 |
5 |
7 |
9 |
|
yn, м |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
30.4. Теоретические сведения
Электрическое поле в проводящей среде создается и поддерживается в стационарном режиме источниками энергии. Такое поле в произвольной точке можно описать законами Ома и Кирхгофа в дифференциальной или интегральной формах:
![]() ;
; ![]() ; rot
; rot![]() ;
; ![]() ;
;
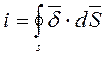 ;
; 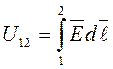 ;
; 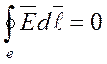 , где
, где ![]() – вектор плотности
электрического тока, A/м,
– вектор плотности
электрического тока, A/м,
![]() – вектор напряженности
электрического поля, В/м,
– вектор напряженности
электрического поля, В/м,
![]() – удельная проводимость
среды, См/м,
– удельная проводимость
среды, См/м,
V– потенциал, В.
При решении задачи по расчету электрического поля заземлителя предполагается, что к нему подведен положительный полюс источника энергии с потенциалом V = U, а отрицательный полюс с потенциалом V = 0 удален на бесконечное расстояние. Среда принята однородной, т.е. удельная проводимость g = const во всех точках. Принятые допущения позволяют упростить решение задачи.
В целом картина электрического поля будет иметь сложный характер. Исходя из условия симметрии можно утверждать, что электрическое поле будет иметь две плоскости симметрии, проходящие вертикально через центр заземлителя: 1) плоскость x – y , совпадающая по направлению с длиной l заземлителя; 2) плоскость x – y, расположенная перпендикулярно длине l заземлителя. В дальнейшем исследование электрического поля проводится в плоскости x – y, совпадающей с длиной l заземлителя.
 Решение
задачи осуществляется методом зеркальных отображений. Сущность метода в данном
случае состоит в том, что непроводящая верхняя часть полупространства
заменяется проводящей средой с такой же удельной проводимостью g и в ней зеркально поверхности раздела располагается заземлитель с
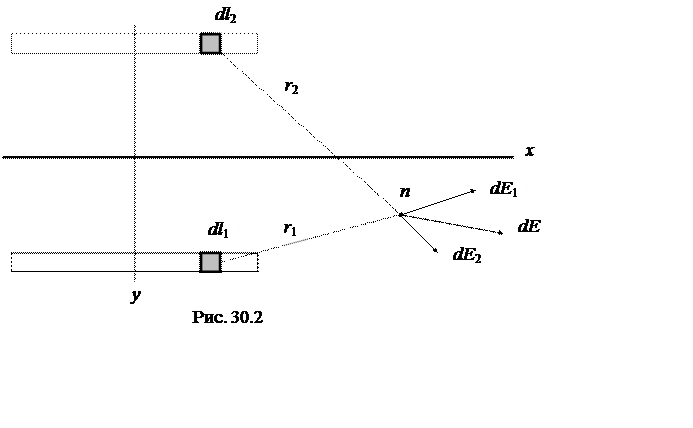
такими же геометрическими и электрическими параметрами (рис. 30.2). Такая
замена не нарушает граничных условий (Ey = 0,
Решение
задачи осуществляется методом зеркальных отображений. Сущность метода в данном
случае состоит в том, что непроводящая верхняя часть полупространства
заменяется проводящей средой с такой же удельной проводимостью g и в ней зеркально поверхности раздела располагается заземлитель с
такими же геометрическими и электрическими параметрами (рис. 30.2). Такая
замена не нарушает граничных условий (Ey = 0, ![]() ), следовательно, не повлияет на распределение
электрического поля в нижней части полупространства.
), следовательно, не повлияет на распределение
электрического поля в нижней части полупространства.
После введения зеркального отображения задача по расчету поля становится симметричной и ее решение упрощается.
Стекание электрического тока с заземлителя будет неравномерным по длине. Линейная плотность тока стекания t будет больше к концам заземлителя и меньше к его середине. В общем случае это будет некоторая функция геометрических размеров l и D и координаты x, умноженная на напряжение U: t=U×f(l, D, x). Вид этой функции должен удовлетворять граничным условиям на поверхности заземлителя: его поверхность должна быть эквипотенциальной с потенциалом V = U = const .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.