результате решения системы уравнений определяются комплексные контурные токи Ik1, Ik2. Токи ветвей I1, I2, I3 определяются через контурные токи: I1 = Ik1, I2 = Ik2, I3 = Ik1 + Ik2. Напряжения на отдельных участках схемы определяются по закону Ома: U1 = I1·Z1, U2 = I2·Z2, U2 = I2·Z2.
Уравнение метода 2-х узлов:
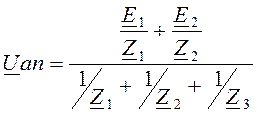 .
.
Токи ветвей I1, I2, I3 определяются из потенциальных уравнений ветвей:
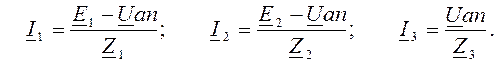
Решение задачи по расчету режима цепи переменного тока, как правило, иллюстрируется построением совмещенной векторной диаграммы напряжений и токов. Для этой цели на комплексной плоскости в выбранных масштабах mU и mI из начала координат откладываются найденные векторы напряжений и токов. Пример построения такой диаграммы в MathCAD приведен на рис. 5.2.
Активные и реактивные мощности отдельных источников и приемников энергии определяются в комплексной форме:
SE1 = P E1 +jQ E1 = E1·I1*, SE2 = P E2 +jQ E2 = E2·I2*, S1 = P 1 +jQ 1 = U1·I1*,
S2 = P 2 +jQ 2 = U2·I2*, S3 = P 3 +jQ 3 = U3·I3*.
Состояние электрической цепи можно описывать потенциальной функцией, разность значений потенциалов в двух заданных точках численно равна напряжению между этими точками: Uab = Va–Vb. При расчете потенциалов точек схемы потенциал одной из них принимают равным нулю, а потенциалы остальных определяют через напряжение между данной точкой и точкой с нулевым потенциалом. Ниже приведен вариант расчета потенциалов точек для исследуемой схемы: Vn = 0 – принимаем; Va= E1; Vb= E1 – I1·R1; Ve= E2; Vd= E2 – I2·jX2; Vf= I3· jX3; Vc= I3·jX3 + I3·R3.
Потенциалы всех характерных точек схемы в выбранном масштабе наносятся на комплексную плоскость в виде точек. Отдельные точки соединяются между собой так, как они соединены на схеме. Таким образом формируется топографическая диаграмма потенциалов. Топографическая диаграмма потенциалов дополняется векторной диаграммой токов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.2. Совмещенная векторная диаграмма напряжений и токов.
Пример построения топографической диаграммы потенциалов и векторной диаграммой токов в MathCAD приведен на рис. 5.3.
При выполнении экспериментальной части работы комплексные ЭДС с заданной начальной фазой через интервал в 120о получаются от симметричного трехфазного генератора: UA = 73×ej0, UB = 73×e-j120, UC = 73×ej120. Комплексные сопротивления ветвей Z = R±jX реализуются путем последовательного включения регулируемого резистора R и регулируемой катушки L при Х > 0 или регулируемого конденсатора C при Х < 0.
Для измерения токов и мощностей в нескольких ветвях цепи применяется коммутатор токовых цепей, позволяющий включать приборы (амперметр и ваттметр) поочередно в любую ветвь цепи.
При измерении начальных фаз векторов токов и напряжений с помощью фазометра следует учитывать, что показание фазометра равно углу сдвига фаз между вектором напряжения U = U×eja и вектором тока I = I×ejb, которые подведены к обмоткам прибора, т.е. j = a-b. Если к фазометру подведен базовый напряжения Uо = U×ej0 с начальной фазой, равной нулю, то показание фазометра будет численно равно j = -b, откуда следует, что b = -j, т.е. начальная фаза вектора тока (аргумент комплекса тока) численно равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.