Лабораторная работа №5
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
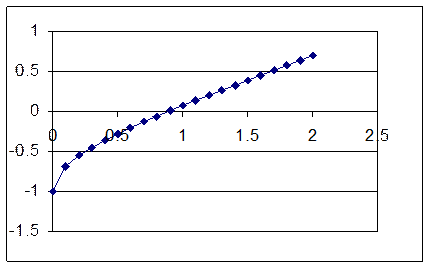 Задана
нелинейная функция, график, построенный в Excel, приведен
на рис.1. Требуется найти один корень, т.к. график пересекает ось абсцисс
только в одной точке на промежутке
Задана
нелинейная функция, график, построенный в Excel, приведен
на рис.1. Требуется найти один корень, т.к. график пересекает ось абсцисс
только в одной точке на промежутке ![]() . Требуется найти эту точку.
. Требуется найти эту точку.
Процесс отыскания корней производится в два этапа:
1.
|
2. Нахождение корней с заданной точностью.

![]() Отделить корень в некоторых случаях можно
и графически. Для этого необходимо построить график соответствующей функции и
найти точку пересечения с осью абсцисс (рис.2).
Отделить корень в некоторых случаях можно
и графически. Для этого необходимо построить график соответствующей функции и
найти точку пересечения с осью абсцисс (рис.2).
Но этот метод может привести к большим погрешностям.
Можно использовать
программный метод. При этом отыскиваются два таких соседних значения ![]() , для которых
, для которых ![]() имеет
противоположные знаки.
имеет
противоположные знаки.
 Зададим код ошибки
равный единице, предполагая, что на отрезки
Зададим код ошибки
равный единице, предполагая, что на отрезки ![]() , где
, где ![]() - левая граница, а
- левая граница, а ![]() -
правая, нет корней. В дальнейшем проверим, так ли это. Затем зададим значение
-
правая, нет корней. В дальнейшем проверим, так ли это. Затем зададим значение ![]() и вычислим значение функции в точке
и вычислим значение функции в точке ![]() . Изменим значение аргумента по формуле
. Изменим значение аргумента по формуле ![]() , где
, где ![]() - шаг
перебора аргумента. Проверим, лежит ли
- шаг
перебора аргумента. Проверим, лежит ли ![]() нутрии
промежутка
нутрии
промежутка ![]() . Если
. Если ![]() , то на
отрезке нет корня. Нужно возвратиться в вызывающую программу. Затем вычисляем
значение функции в новой точке
, то на
отрезке нет корня. Нужно возвратиться в вызывающую программу. Затем вычисляем
значение функции в новой точке ![]() и проверяем, изменила
ли функция знак или нет. Если нет, то опять изменяем
и проверяем, изменила
ли функция знак или нет. Если нет, то опять изменяем ![]() .
Если да, то определяем границы отрезка
.
Если да, то определяем границы отрезка ![]() по
формулам
по
формулам ![]() ,
, ![]() . В
данном случае код ошибки равен единице, отрезок найден (рис. 3).
. В
данном случае код ошибки равен единице, отрезок найден (рис. 3).
Для уточнения корня нелинейного уравнения до заданной точности используем два метода:
1. Метод половинного деления. 2.Метод Ньютона.
Метод половинного деления
Данный метод
заключается в разбиении отрезка пополам при условии, если корень попадает в
данный отрезок. Эту операцию можно повторять несколько раз до получения
заданной точности. Зададим код ошибки равный единице. Проверим произведение ![]() , если знак положительный, то возвращаемся
в вызывающую программу. Зададим границы отрезка содержащего корень
, если знак положительный, то возвращаемся
в вызывающую программу. Зададим границы отрезка содержащего корень ![]() ,
, ![]() ;
зададим начальное
;
зададим начальное  значение итерации
значение итерации ![]() , код ошибки равен нулю.
Вычислим значение функции в точке
, код ошибки равен нулю.
Вычислим значение функции в точке ![]() . Вычислим середину
отрезка
. Вычислим середину
отрезка ![]() :
: ![]() . Изменим,
счетчик итераций на
. Изменим,
счетчик итераций на ![]() . Если длина отрезка
. Если длина отрезка ![]() меньше заданной точности, то возвращаемся
в вызывающую программу. Необходимо проверить, в каком из отрезков
меньше заданной точности, то возвращаемся
в вызывающую программу. Необходимо проверить, в каком из отрезков ![]() или
или ![]() лежит
корень. Если корень лежит внутри первого отрезка, то изменяем правую границу
отрезка, в противном случае – левую: если
лежит
корень. Если корень лежит внутри первого отрезка, то изменяем правую границу
отрезка, в противном случае – левую: если![]() , то
, то ![]() , иначе
, иначе ![]() (рис.4).
(рис.4).
Метод Ньютона
Метод состоит в построении
итерационной последовательности 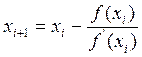 , сходящейся к корню
уравнения
, сходящейся к корню
уравнения ![]() (рис. 5). Зададим код ошибки равный
единице, и изначальное количество итераций
(рис. 5). Зададим код ошибки равный
единице, и изначальное количество итераций ![]() ,
текущее значение корня
,
текущее значение корня ![]() . Выполним итерационный цикл, изменим,
количество итераций на
. Выполним итерационный цикл, изменим,
количество итераций на ![]() , если количество итераций
превысило
, если количество итераций
превысило ![]() , осуществим возврат в вызывающую
программу, вычислим уточненное значение по формуле:
, осуществим возврат в вызывающую
программу, вычислим уточненное значение по формуле: 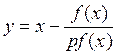 ,
вычислим модуль разности
,
вычислим модуль разности ![]() . В качестве нового
значения зададим уточненное значение корня
. В качестве нового
значения зададим уточненное значение корня ![]() . Если
. Если ![]() , то итерационный цикл необходимо
повторить. После достижения заданной точности, код ошибки, меняем на ноль и
осуществляем возврат в вызывающую программу.
, то итерационный цикл необходимо
повторить. После достижения заданной точности, код ошибки, меняем на ноль и
осуществляем возврат в вызывающую программу.
На языке Fortran программа примет следующий вид:
Function F(x)
F=sqrt(x)-cos(.387*x)
end
Function PF(x)
PF=1/(2*sqrt(x))+.387*sin(.387*x)
end
Program L5
External F,PF
x0=0.5
do ; call OKNU(F,x0,1.5,0.1,a,b,ier1); if(ier1==1) exit
print*,a,b,ier1 ; x0=b
call MPD(F,a,b,1E-5,C,ier2)
print*,C,ier2
call MN(F,PF,0.5*(a+b),1E-5,20,C1,ier3)
print*,C1,ier3
enddo
End
Subroutine OKNU(F,XL,XR,h,a,b,ier)
X=XL; y=F(x); ier=1
do; x=x+h; if(x>XR) Return
Z=F(x); if(y*Z<=0) then
ier=0; a=x-h; b=x;
return; end if
enddo
End
Subroutine MPD(F,a1,b1,eps,c,ier)
a=a1; b=b1
ier=1; if(F(a)*F(b)>0) Return
ier=0; y=F(a)
do; c=0.5*(a+b)
if(y*F(c)>0) then; a=c; else; b=c; end if
if(b-a<eps) Return
enddo
End
Subroutine MN(F,FP,x0,eps,mmax,x,ier)
x=x0; m=0
do; m=m+1; if(m>mmax) Return
y=x-F(x)/FP(x); e=abs(y-x); x=y
if(e<eps) then; ier=0; Return; end if
enddo
End
|
8.000001E-01 |
9.000001E-01 |
0 |
|
8.867738E-01 |
0 |
|
|
8.867772E-01 |
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.