Лабораторная работа №6
Вычисление определённых интегралов
 Постановка
задачи: Вычислить определённый интеграл от функции
Постановка
задачи: Вычислить определённый интеграл от функции ![]() ,
используя: метод трапеции, метод прямоугольника, метод Симпсона, метод Гаусса.
,
используя: метод трапеции, метод прямоугольника, метод Симпсона, метод Гаусса.
Обыкновенный
определённый интеграл считается по формуле Ньютона-Лейбница ![]() . Численное интегрирование применяется,
если нахождение
. Численное интегрирование применяется,
если нахождение ![]() сложно и невозможно.
сложно и невозможно.
Рассмотрим несколько методов вычисления определенного интеграла.
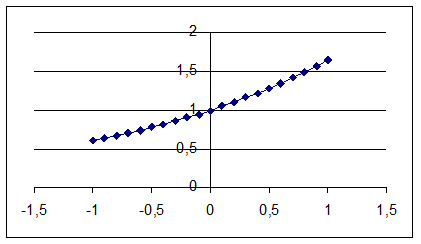
Построим график функции в
![]() Exile. Он представлен
на рис. 1, на интервале
Exile. Он представлен
на рис. 1, на интервале ![]() .
.
 Метод
прямоугольников
Метод
прямоугольников
Метод
прямоугольника заключается в разбиении отрезка интегрирование на ![]() промежутков
промежутков ![]() (рис.2),
где
(рис.2),
где ![]() ,
, ![]() - шаг
разбиения. Применяя формулу прямоугольника к каждому промежутку и суммируя,
получим
- шаг
разбиения. Применяя формулу прямоугольника к каждому промежутку и суммируя,
получим
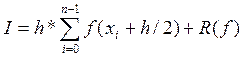 ,
,
![]()
![]() -
остаточный член. Для метода прямоугольника
-
остаточный член. Для метода прямоугольника ![]() .
.
Текст программы
Program L5
EXTERNAL F
n=20; a=-1; b=1
Call MP(F,a,b,n,y)
Print '(I5,a1,F10.5)',n,char(9),y
Do; n=n+2; Call MP(F,a,b,n,y1)
e=abs(y1-y); y=y1
Print '(I5,a1,F10.5)',n,char(9),y
If(e<1E-5) exit
Enddo
End
SUBROUTINE MP(F,a,b,n,y)
h=(b-a)/n; y=0
Do i=0, n-1; x=a+i*h+h/2
y=y+F(x)
Enddo
y=y*h
End
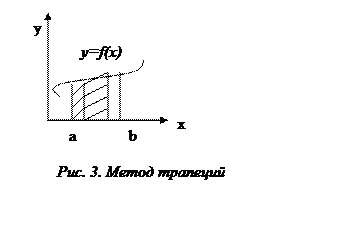 Метод трапеций
Метод трапеций
Данный метод заключается в том, что данную криволинейную трапецию разбиваем не на прямоугольники, а на прямолинейные трапеции и соответственно используем не формулу площади прямоугольника а площади трапеции (рис. 3).
Суммируя площади трапеций, получим численное значение определенного интеграла.
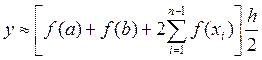
Текст программы
Program L5
EXTERNAL F
n=20; a=-1; b=1
Call MT(F,a,b,n,y)
Print '(I5,a1,F10.5)',n,char(9),y
Do; n=n+2; Call MT(F,a,b,n,y1)
e=abs(y1-y); y=y1
Print '(I5,a1,F10.5)',n,char(9),y
If(e<1E-5) exit
Enddo
End
Function F(x)
F=sqrt(exp(x))
End
SUBROUTINE MT(F,a,b,n,y)
h=(b-a)/n; y=0
Do i=1, n-1; x=a+i*h
y=y+F(x)
Enddo
y=(y+(F(a)+F(b))/2)*h
End
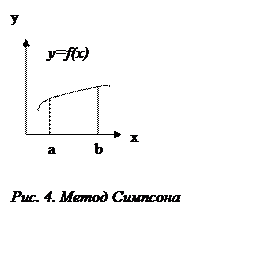 Метод Симпсона
Метод Симпсона
Метод Симпсона
или метод парабол заключается в том, что через три точки в плоскости можно
провести только одну параболу. На кривой можно найти точки, через которые и
проведем эти параболы. Криволинейная трапеция разобьется на маленькие криволинейные
трапеции, ограниченные сверху этими параболами. Число отрезков, на которые
разбиваем интервал, должно быть четным (рис. 4). Выполняя эти операции, можем
записать следующие формулы 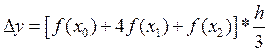 .
.
Если
просуммировать данные площади, то получим: 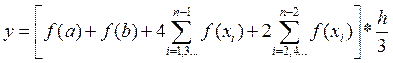 или
иначе можно записать:
или
иначе можно записать: 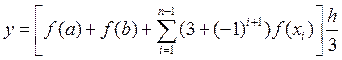
Текст программы
Program L5
EXTERNAL F
n=20; a=-1; b=1
Call MS(F,a,b,n,y)
Print '(I5,a1,F10.5)',n,char(9),y
Do; n=n+2; Call MS(F,a,b,n,y1)
e=abs(y1-y); y=y1
Print '(I5,a1,F10.5)',n,char(9),y
If(e<1E-5) exit
Enddo
End
Function F(x)
F=sqrt(exp(x))
End
SUBROUTINE MS(F,a,b,n,y)
h=(b-a)/n; y=0; c=1
Do i=1, n-1; x=a+i*h
y=y+F(x)*(3+c); c=-c
Enddo
y=(y+F(a)+F(b))*h/3.
End
Метод Гаусса
Основан на интерполяции f(x) полиномом Лагранжа. Интеграл вычисляется по 8 точкам.
Program L5
EXTERNAL F
n=20; a=-1; b=1
Call Qg8(a,b,F,y)
Print '(I5,a1,F10.5)',n,char(9),y
Do; n=n+2; CallQg8(a,b,F,y1)
e=abs(y1-y); y=y1
Print '(I5,a1,F10.5)',n,char(9),y
If(e<1E-5) exit
Enddo
End
Результаты вычислений приведены в таблице
|
n |
MP |
MT |
Qg8 |
n1 |
MS |
|
20 |
2.08416 |
2.08482 |
2.08438 |
2 |
2.08508 |
|
40 |
2.08433 |
2.08449 |
4 |
2.08443 |
|
|
60 |
2.08436 |
2.08443 |
6 |
2.08439 |
|
|
80 |
2.08437 |
2.08441 |
8 |
2.08438 |
|
|
100 |
2.08440 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.