


Лабораторная работа №6
Вычисление определённых интегралов
Порядок выполнения задания:
1) составить программное обеспечение: подпрограммы вычисления интеграла методами прямоугольников, трапеций, Симпсона, Гаусса; подпрограмму-функцию для вычисления значений f(x);
2) составить головную программу для исследования точности вычисления интеграла разными методами;
3) выбрать исходные данные и провести счёт;
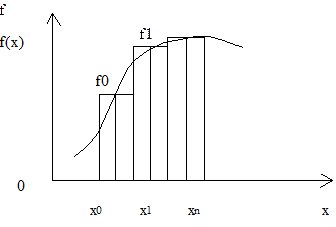
Метод прямоугольников.
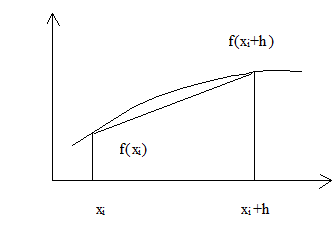
 На
каждом промежутке
На
каждом промежутке ![]() функция y=f(x)
заменяется интерполяционным многочленом нулевого порядка, построенным по
значению функции в средней точке xi+h/2. Применяя формулу прямоугольников к каждому
промежутку и суммируя, получим
функция y=f(x)
заменяется интерполяционным многочленом нулевого порядка, построенным по
значению функции в средней точке xi+h/2. Применяя формулу прямоугольников к каждому
промежутку и суммируя, получим
I=h*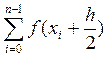 +R(f)
+R(f)
где R(f) – остаточный член, который не используется в вычислениях, но по которому можно судить о точности применяемой формулы. Для метода прямоугольников R(f)=h2*(b-a)*f’’(t)/24, f’’(t) – значение второй производной f(x) в точке x=t, где она максимальна.
Метод трапеций.
Метод трапеций заключается в линейном аппроксизме f(x) на промежутке [xi,xi+1]. С учётом суммирования смежных ординат внутри отрезка [a,b] обобщённая формула принимает вид:
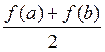 +
+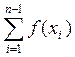 }-R(f),
}-R(f),где R(f)=h2*(b-a)*f¢¢(t)/12
Метод Симпсона (парабол):
Метод Симпсона является частным случаем метода Ньютона-Котеса. Последний основан на интерполяции f(x) в m промежутках (т.е. на участке [xi,xi+m]) полиномом Лагранжа. При этом f(x) должна задаваться (m+1) ординатами. Формулы интегрирования точны, если f(x)-многочлен m-ой степени. При m=1 получаем метод трапеций, при m=2-метод Симпсона. Интеграл от xi до xi+2 от полинома Лагранжа, проходящего через точки (xi,f(x)),(xi+1,f(xi+1)),(xi+2,f(xi+2)),равен
[f(xi+4*f(xi+1)+f(xi+2)]*h/3.)
При суммировании получим обобщённую формулу Симпсона:
 I=
I=![]() *{f(a)+f(b)+4*
*{f(a)+f(b)+4*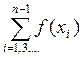 +2*
+2*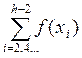 }-R(f), где
R(f)=n*h5*f¢(t)/90.
Формулу можно представить в следующем виде:
}-R(f), где
R(f)=n*h5*f¢(t)/90.
Формулу можно представить в следующем виде:
I=h/3*{f(a)+f(b)+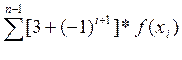 }-R(f)
}-R(f)
При использовании приведённых формул необходимо помнить, что число разбиений n в методе Симпсона должно быть чётным.
Метод Гаусса:
Метод Гаусса основан на интерполяции f(x) полиномом Лагранжа, но абсциссы x выбираются из условия обеспечения минимума погрешности интерполяции. Квадратурная формула Гаусса имеет вид:
I=![]() *
*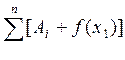 +R(f),
где x1=
+R(f),
где x1=![]() +
+![]() *t1,
*t1,
t1 - углы квадратичной формулы Гаусса, Ai - гауссовые коэффициенты, n-число узлов квадратичной формулы. Узлы t1 являются корнями многочленов Лагранжа степени n и расположены симметрично на отрезке [-1,1]. Гауссовые коэффициенты Ai равны для симметрично расположенных узлов. Метод Гаусса обеспечивает наивысший порядок точности - формула точности для многочленов степени не выше (2n-1).
Исходные данные:
f(x)=(exp(x)), a=-1, b=1
Решение в Fortran:
program pr
external F
n=4;e=1;a=-1;b=1
call met_pr(F,a,b,n,y1)
call met_tr(F,a,b,n,y2)
call met_sim(F,a,b,n,y3)
call qg8(a,b,f,y)
print*,' n met_pr met_tr met_sim met_Gauss'
print*,n,y1,y2,y3,y
y11=0;y22=0;y33=0
do
n=n+4
call met_pr(F,a,b,n,y1)
call met_tr(F,a,b,n,y2)
call met_sim(F,a,b,n,y3)
print*,n,y1,y2,y3
e1=abs(y1-y11);y11=y1
e2=abs(y2-y22);y22=y2
e3=abs(y3-y33);y33=y3
if(e1<1e-6.and.e2<1e-6.and.e3<1e-6)exit
! if(y1==y.and.y2==y.and.y3==y)exit
enddo
end
Программы:
subroutine met_pr(F,a,b,n,y1)
real::F,a,b,y1,h,x,h2
integer::i,n
h=(b-a)/n;h2=h/2;y1=0
do i=0,n-1
x=a+i*h+h2
y1=y1+f(x)
enddo
y1=y1*h
end
subroutine met_tr(F,a,b,n,y2)
real::F,a,b,y2,h,x
integer::i,n
h=(b-a)/n;y2=0
do i=1,n-1
x=a+i*h
y2=y2+f(x)
enddo
y2=((f(a)+f(b))/2+y2)*h
end
subroutine met_sim(F,a,b,n,y)
real::F,a,b,y,h,x
integer::i,n
h=(b-a)/n;y=0;c=1
do i=1,n-1
x=a+i*h
y=y+(3+c)*f(x)
c=-c
enddo
y=(f(a)+f(b)+y)*h/3
end
subroutine qg8(xl,xv,f,y)
a=.5*(xv+xl)
b=(xv-xl)
c=.4801449*b
y=.05061427*(f(a+c)+f(a-c))
c=.3983332*b
y=y+.1111905*(f(a+c)+f(a-c))
c=.2627662*b
y=y+.1568533*(f(a+c)+f(a-c))
c=.09171732*b
y=b*(y+.1813419*(f(a+c)+f(a-c)))
return
end
function f(x);f=exp(x);
end
Результатысчёта:
N met_pr met_tr met_sim met_Gauss
4 2.326097 2.399166 2.351195 2.350402
8 2.344293 2.362631 2.350453
12 2.347684 2.355841 2.350413
16 2.348873 2.353462 2.350406
20 2.349423 2.352361 2.350404
24 2.349722 2.351763 2.350403
28 2.349903 2.351402 2.350403
32 2.350020 2.351167 2.350402
36 2.350100 2.351007 2.350403
40 2.350158 2.350892 2.350403
44 2.350200 2.350807 2.350403
48 2.350233 2.350743 2.350403
52 2.350258 2.350693 2.350403
56 2.350278 2.350652 2.350403
60 2.350294 2.350620 2.350403
Решениев Mathcad:
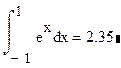
Наиболее эффективным методом нахождение интегралов в Fortran является метод Гауса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.