Определяем
изгибающий момент ![]() и поперечную силу
и поперечную силу ![]() в
в ![]() пролета
простой балки. Сечение, расположенное в
пролета
простой балки. Сечение, расположенное в ![]() пролета,
отстоит на расстоянии
пролета,
отстоит на расстоянии 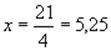 м от левой опоры:
м от левой опоры:
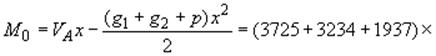
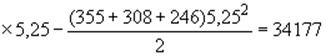 кгсм,
кгсм,
![]()
![]() кгс.
кгс.
По
табл.1 Руководства определяем ординату оси свода в ![]() пролета
и
пролета
и ![]() в этом сечении:
в этом сечении:
![]() м;
м; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Максимальный
положительный изгибающий момент в ![]() пролета на левой
половине свода
пролета на левой
половине свода
![]() кгсм.
кгсм.
Нормальная
сила в ![]() пролета на левой половине свода
пролета на левой половине свода
![]()
![]() кгс.
кгс.
Определяем
максимальный отрицательный изгибающий момент в ![]() пролета
на правой половине свода
пролета
на правой половине свода
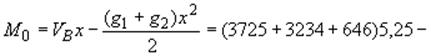
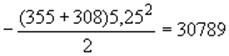 кгсм;
кгсм;
![]()
![]() кгс;
кгс;
![]() кгсм.
кгсм.
![]() кгс.
кгс.
Проверка прочности волны свода при внецентренном сжатии в сечениях с максимальными положительным и отрицательным изгибающими моментами
(производится по СНиП II-В.2-71*, "Каменные и армокаменные конструкции. Нормы проектирования"**)
________________
* При введении в действие новой редакции главы СНиП расчет свода на внецентренное сжатие производится по измененной редакции.
________________
** Внимание! Документ недействующий. Действует СНиП "Каменные и армокаменные конструкции. Нормы проектирования". - Примечание "КОДЕКС".
а) Расчет волны свода на левой половине пролета в сечении с максимальным положительным моментом:
расчет производим по формуле
![]() ,
,
![]() =1 (см. примечание 4 к п.5.9 Руководства).
=1 (см. примечание 4 к п.5.9 Руководства).
Расчетное
сопротивление кладки свода ![]() =22,5 кгс/см
=22,5 кгс/см![]() .
.
Коэффициент продольного изгиба при внецентренном сжатии определяется по формуле
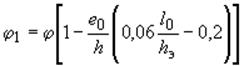 .
.
Длина
оси свода при 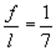 определяется по табл.4
Руководства
определяется по табл.4
Руководства
![]() м.
м.
Расчетная длина свода при продольном изгибе (п.5.9 Руководства)
![]() м.
м.
Радиус
инерции поперечного сечения свода принимается по табл.3 Руководства ![]() =21,2 см.
=21,2 см.
Гибкость
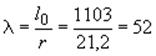 .
.
Коэффициент
продольного изгиба при центральном сжатии ![]() =0,77.
=0,77.
Эксцентрицитет приложения нормальной силы
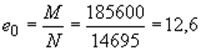 см.
см.
Расстояние от оси, проходящей через центр тяжести сечения до края сечения в сторону эксцентриситета (см. табл.3 Руководства)
![]() см,
см, 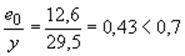 ;
;
![]() см;
см;
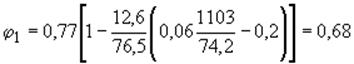 .
.
Коэффициент
![]() определяется по формуле
определяется по формуле
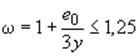 .
.
Если
![]() , то вместо
, то вместо ![]() принимается
принимается
![]() . В данном случае
. В данном случае ![]() см,
поэтому
см,
поэтому
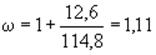 .
.
Величину
площади сжатой зоны сечения ![]() , центр тяжести которой
совпадает с точкой приложения нормальной силы, отстоящей на расстоянии
, центр тяжести которой
совпадает с точкой приложения нормальной силы, отстоящей на расстоянии ![]() см от нижнего края сечения, определяем
последовательным приближением (см. п.5.9 Руководства).
см от нижнего края сечения, определяем
последовательным приближением (см. п.5.9 Руководства).
Для
первого приближения принимаем, что расстояние от нижнего края сечения до
границы сжатой зоны ![]()
![]() см
(см. п.5.9 рис.25, а Руководства).
см
(см. п.5.9 рис.25, а Руководства).
Высота сжатой зоны сечения:
![]() см;
см;
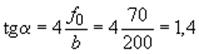 ;
; ![]() ,
, ![]() ;
;
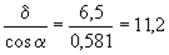 см;
см; 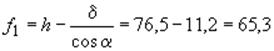 см;
см;
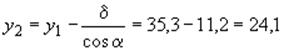 см;
см;
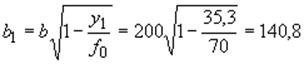 см;
см;
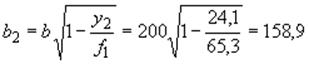 см.
см.
Площадь, ограниченная параболой 1, 2, 3:
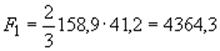 см
см![]() .
.
Площадь, ограниченная параболой 4, 5, 6:
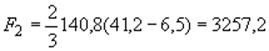 см
см![]() .
.
Площадь сжатой зоны сечения:
![]() см
см![]() .
.
Проверяем
точность приближенного определения площади ![]() .
.
Расстояние
центра тяжести площади ![]() от нижнего края сечения:
от нижнего края сечения:
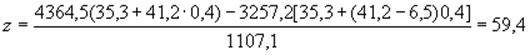 см;
см;
![]() см.
см.
Несущая способность сечения
![]() кгс
кгс ![]() кгс.
кгс.
Несущая способность сечения обеспечивается с запасом.
б) Расчет волны свода на правой половине пролета в сечении с максимальным отрицательным моментом.
Эксцентрицитет приложения нормальной силы:
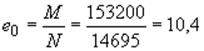 см.
см.
Расстояние
от оси, проходящей через центр тяжести сечения до края сечения в сторону
эксцентрицитета ![]() =47 см:
=47 см:
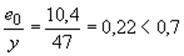 ;
;
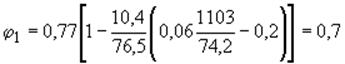 ;
;
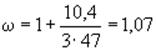 .
.
В
данном случае 3![]() =3·47=141 см>1,5
=3·47=141 см>1,5![]() =1,5·76,5=114,8 см.
=1,5·76,5=114,8 см.
Площадь
сжатой зоны сечения ![]() , центр тяжести которой совпадает
с точкой приложения нормальной силы, отстоящей на расстоянии
, центр тяжести которой совпадает
с точкой приложения нормальной силы, отстоящей на расстоянии ![]() =47-10,4=36,6 см от нижнего края сечения
(см. п.5.9 и рис.25, б Руководства); определяем последовательным приближением.
=47-10,4=36,6 см от нижнего края сечения
(см. п.5.9 и рис.25, б Руководства); определяем последовательным приближением.
Для первого приближения принимаем, что расстояние от нижнего края сечения до границы сжатой зоны (высота сжатой зоны):
![]() см,
см,
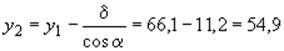 см;
см;
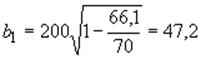 см;
см;
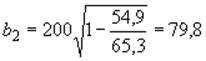 см.
см.
Площадь прямоугольника 1, 2, 4, 5:
![]() см
см![]() .
.
Площадь, ограниченная параболой 2, 3, 4:
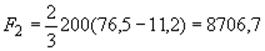 см
см![]() .
.
Площадь, ограниченная параболой 6, 3, 7:
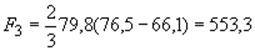 см
см![]() .
.
Площадь, ограниченная параболой 8, 9, 10:
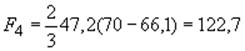 см
см![]() .
.
Площадь, ограниченная параболой 1, 9, 5:
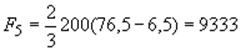 см
см![]() ;
;
![]()
![]() см
см![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.