Руководство по проектированию и возведению каменных сводов двоякой кривизны, страница 11

Наибольшая величина эксцентрицитета приложения нормальной силы в сводах 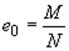 не должна превышать: для основных сочетаний нагрузок 0,7, где  - расстояние от оси , проходящей через центр тяжести сечения до края сечения в сторону эксцентрицитета (при положительном изгибающем моменте , при отрицательном моменте , см. табл.3).

Величину площади сжатой зоны сечения  определяют последовательным приближением из условия совпадения центра тяжести сжатой зоны с точкой приложения силы  (рис.25).

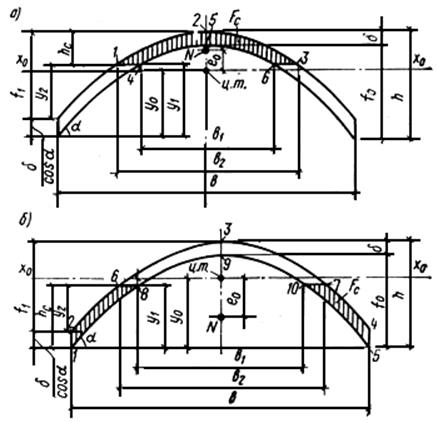
Рис.25. Сжатая зона поперечного сечения свода

а - при приложении нормальной силы выше оси, проходящей через центр тяжести сечения; б - при приложении нормальной силы ниже оси, проходящей через центр тяжести сечения

При приложении нормальной силы выше оси, проходящей через центр тяжести поперечного сечения волны свода (при положительном изгибающем моменте, рис.25 а), величину площади сжатой зоны  определяют как разность площадей, ограниченных параболами 1, 2, 3 и 4, 5, 6*, задаваясь расстоянием от нижней грани сечения до границы сжатой зоны .

________________

* Площадь, ограниченная параболой, равна  произведения основания параболы на ее высоту.

Расстояние от центра тяжести сжатой зоны до нижней грани сечения определяется как отношение разности статических моментов площадей, ограниченных параболами 1, 2, 3 и 4, 5, 6, относительно нижней грани сечения к площади *. Если центр тяжести площади  не совпадает с точкой приложения нормальной силы, отстоящей на расстоянии  от нижней грани сечения, то задаются другим значением  и вновь определяют площадь сжатой зоны и положение ее центра тяжести.

________________

* Расстояние центра тяжести площади, ограниченной параболой от ее основания, равно 0,4 высоты параболы.

При расчете сечения принимают то значение площади , при котором ее центр тяжести достаточно близко совпадает с точкой приложения нормальной силы (). Для первого приближения можно принять .

При приложении нормальной силы ниже оси, проходящей через центр тяжести поперечного сечения волны (при отрицательном изгибающем моменте, рис.25, б), площадь сжатой зоны сечения  и статический момент ее относительно нижней грани сечения при принятом значении  определяют как сумму и разность следующих площадей и их статических моментов: 1, 2, 4, 5 (прямоугольник) + 2, 3, 4-6, 3, 7+8, 9, 10-1, 9, 5.

Расстояние от центра тяжести площади  до нижней грани сечения  определяется как отношение сумм и разностей статических моментов указанных выше площадей к площади .

Значение  подбирается таким, чтобы обеспечивалось близкое совпадение центра тяжести площади  с точкой приложения нормальной силы (). Для первого приближения можно принять .

Размеры оснований парабол определяют по формулам:

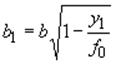;                                                        (7)

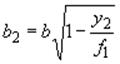.                                                    (8)

Обозначения величин, входящих в формулы (7) и (8), приведены на рис.25.

Угол , необходимый для вычисления высоты параболы 2, 3, 4 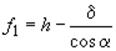, и величины  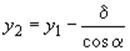определяются по величине

.

Расчетные сопротивления кладки сводов, модули упругости кладки (начальные модули деформации) и коэффициенты продольного изгиба принимают по главе СНиП "Каменные и армокаменные конструкции. Нормы проектирования". При этом расчетные сопротивления кладки кирпичных сводов толщиной  кирпича увеличивают путем умножения на коэффициент 1,25. Модуль деформаций кладки сводов принимается =0,5 , где  - модуль упругости кладки.

Расчетную длину сводов  при определении коэффициентов продольного изгиба принимают равной 0,5, где  - длина оси свода, определяемая по табл.4.

ТАБЛИЦА 4 

Примечания: 1. При применении сводов с размерами поперечных сечений, не включенных в табл.3, необходимо, чтобы размеры сечений удовлетворяли требованиям п.2.5 настоящего Руководства.