


Пусть имеется ДСВ, принимающая неотрицательные целочисленные значения 0,1,2,…,k,… с вероятностью p0, p1, …, pk, …, где pk=p{x=k}.
Определение. Производящей функцией для ДСВ называют функцию вида:
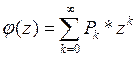 , (*)
, (*)
где z - произвольный параметр (![]() ).
).
Коэффициент при zk в ней
равен вероятности того, что ДСВ примет значение ![]() .
.
Ясно, что при z=1
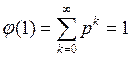 - это условие полноты.
- это условие полноты.
Замечание. При конечных значениях ДСВ x (*) сохраняет силу.
Возьмем первую производную по z от (*)
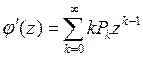
Положим z = 1.
Имеем ![]()
![]()
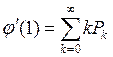
Известно, что это математическое ожидание ДСВ, отсюда
![]() . Так можно найти математическое
ожидание!!!
. Так можно найти математическое
ожидание!!!
Возьмем вторую производную по z от (*). Имеем
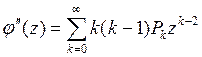
Полагая здесь z=1, получим
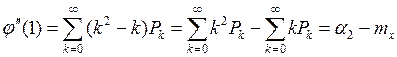
Отсюда
![]()
Можно показать, что
![]()
Это позволяет выразить начальные моменты более высокого уровня через моменты более низкого уровня!!!
Рассмотрим конкретные законы ДСВ
1) Для биномиального распределения производящая функция имеет вид:
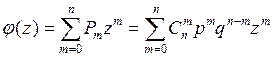 - n-ая степень
бинома, где q=(1-p)
- n-ая степень
бинома, где q=(1-p)
Тогда ![]()
Найдем производную по z
![]()
при z=1, получим
![]()
И мы уже знаем, что 2-й начальный момент можно найти как
![]()
![]() .
.
Отсюда
![]() .
.
Тогда
![]() .
.
Для дисперсии имеем
![]()
Замечание. Для обобщенного биномиального
распределения, то есть когда ![]() и т.д.
и т.д.
![]() .
.
Перемножая биномы и приводя подобные члены с одинаковыми степенями z мы действительно получим
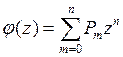 и
и 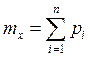 ,
, 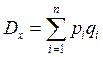
2) Для распределения Пуассона имеем
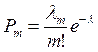 , m=0,1,2,…
, m=0,1,2,…
Отсюда для производящей функции
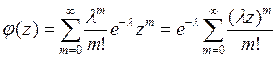 , где
, где 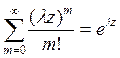
Поэтому
![]()
Для
![]()
При z=1 получим
![]()
Для второй производной имеем
![]() и
и ![]()
Отсюда, для ![]() получим
получим
![]() , а для Dx найдем
, а для Dx найдем
![]()
То есть, только в Пуассоновском распределении
![]()
- это замечательное свойство этого распределения.
3) Для геометрического распределения с "0" имеем
![]() (q=1-p) – это число "безуспешных" попыток или до первого
появления "успеха" с вероятностью p.
(q=1-p) – это число "безуспешных" попыток или до первого
появления "успеха" с вероятностью p.
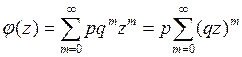
Здесь ![]() и имеем бесконечно
убывающую геометрическую прогрессию со знаменателем qz,
а ее сумма равна
и имеем бесконечно
убывающую геометрическую прогрессию со знаменателем qz,
а ее сумма равна 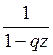
Тогда
![]()
![]()
![]()
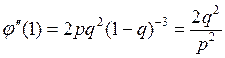
Отсюда 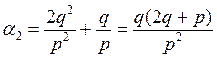 , но
, но ![]() и тогда
и тогда 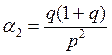
Для дисперсии получим
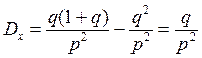
Для геометрического распределения с "1"
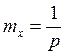
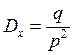 , так
как это ДСВ вида x+1
, так
как это ДСВ вида x+1
и можно найти значения с использованием свойств математического ожидания и дисперсии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.