Построение одноаргументных моделей на основе экспериментальных исследований характеристик объекта

Отчет по лабораторной работе №1.

Построение одноаргументных моделей на основе экспериментальных исследований характеристик объекта.

1)   Построение линейной модели объекта «Полкан».

Линейная модель имеет вид   , где х-входная переменная, y-выходная.

Экспериментальные значения:

X	Y
0	1.
0.1	1.21
0.2	1.48
0.3	1.56
0.4	1.76
0.5	1.36
0.6	2.21
0.7	2.38
0.8	2.64
0.9	2.56
1	2.96

С помощью программы “Origin” мы выстроили  точки и аппроксимировали их функцией “Fit Linear“, то есть   линейной зависимостью.

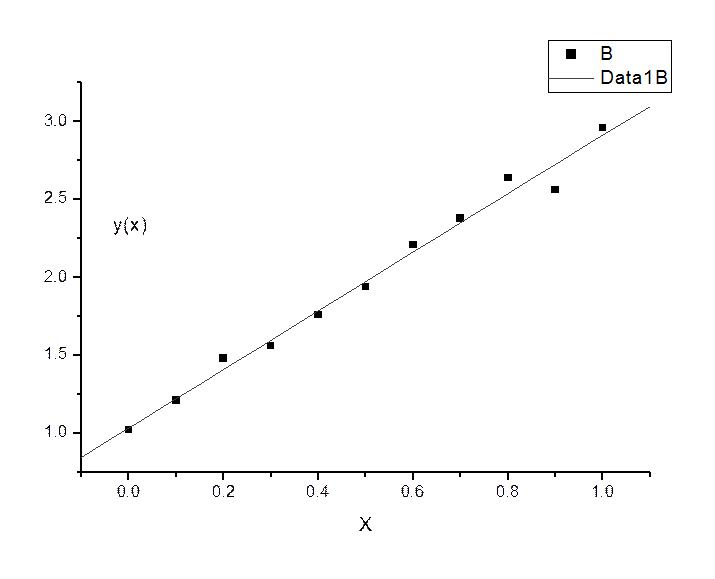
Выше приведен рисунок аппроксимации и ниже параметры:

SD=0.07586 – среднеквадратичное отклонение;

a₀  = 1.035;

a₁    = 1.87909;

Также задача была выполнена с помощью функции Aprline методом наименьших квадратов.

Считанные данные:

n = 11

i        X         Y

1      0.00    1.02

2      0.10    1.21

3      0.20    1.48

4      0.30    1.56

5      0.40    1.76

6      0.50    1.94

7      0.60    2.21

8      0.70    2.38

9      0.80    2.64

10      0.90    2.56

11      1.00    2.96

Err = 0

A0 = 1.035

A1 = 1.879091

S = 0.075859

Тоже самое мы проделали с помощью «Mathcad».

Для определения разброса параметра Y проводим дополнительный эксперимент: в центре диапазона моделирования  выбираем точку и несколько раз измеряем значения y при постоянном значении x=0.5. Данные измерения занесены в таблицу Excel и с помощью функии «дисп.» вычислено значение дисперсии. 

X	Y	Дисп. Y	Среднеквад.	Дисп. адекват.	Дис.ад/дисп.Y
0.5	1.94	0.013	0.076	0.006	0.452
	1.97
	2.02
	1.88
	1.97
	2.08
	2.15
	1.81
	2.13

Для проверки адекватности модели было вычислено отношение дисп.ад/диспY . Оно составило 0.452. Это значение было сравнено с критерием Фишера, вычисленного для вероятности 0.98. При вычислении критерия Фишера были взяты следующие параметры:

Число степеней свободы верхней дисперсии=

число точек в эксперименте- число параметров = 11-2=9;

Число степеней свободы нижней дисперсии=

число точек в эксперименте для определения разброса 10– 1=9.

Доверительная вероятность=0.98.

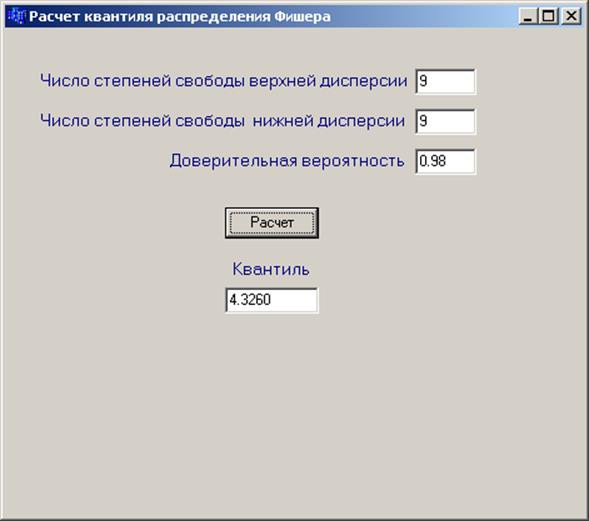
Квантиль=4.326.

Так как отношение дисперсии меньше критерия Фишера, то эти дисперсии  статистически неразличимы и модель можно считать адекватной.

С помощью программы “Origin” мы выстроили  точки и аппроксимировали их функцией “Fit Polnomial“, то есть полиномом 3-ей степени.

0	1.62
0.1	4.93
0.2	5.35
0.3	4.32
0.4	3.75
0.5	1.87
0.6	-0.3
0.7	-0.01
0.8	0.05
0.9	3.85
1	7.8

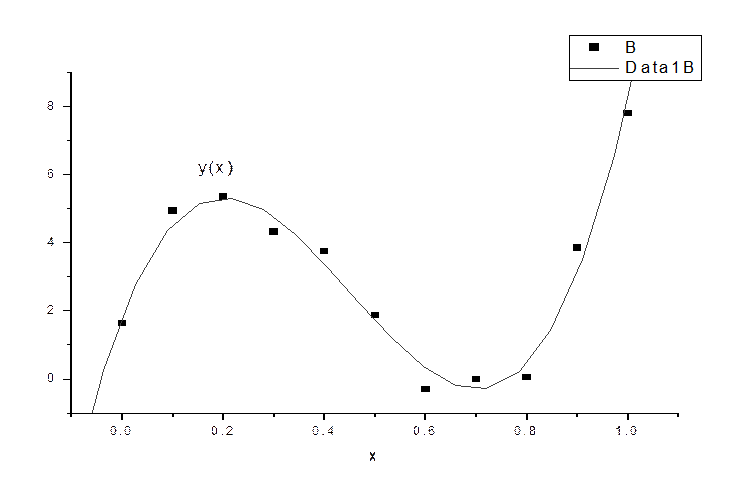
Выше приведен рисунок аппроксимации и ниже параметры:

SD=0.07586 – среднеквадратичное отклонение;

a₀  = 1.035;

a₁    = 1.87909;