Также задача была выполнена с помощью функции Aprline методом наименьших квадратов.
A 1.83804 0.46066
B1 38.2899 4.19485
B2 -122.25583 10.04679
B3 90.28166 6.5932
-----------------------------------------------------------SD=0.51821
Считанные данные:
n = 11
i X Y
1 0.00 1.62
2 0.10 4.93
3 0.20 5.35
4 0.30 4.32
5 0.40 3.75
6 0.50 1.87
7 0.60 -0.30
8 0.70 -0.01
9 0.80 0.05
10 0.90 3.85
11 1.00 7.80
A0 = 1.838042
A1 = 38.289899
A2 = -122.255828
A3 = 90.281663
S = 0.51821
Результаты вычислений в программе «Matchad» представлены ниже:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
Дисп. Y |
Среднеквад. |
Дисп. адекват. |
Дис.ад/дисп.Y |
||||
|
0.5 |
2.1 |
0.429 |
0.076 |
0.006 |
0.013 |
||||
|
1.94 |
|||||||||
|
2.73 |
|||||||||
|
2.05 |
|||||||||
|
1.04 |
|||||||||
|
1.39 |
|||||||||
|
2.74 |
|||||||||
|
0.91 |
|||||||||
|
1.77 |
|||||||||
Для проверки адекватности модели было вычислено отношение дисп.ад/диспY . Оно составило 0.013. Это значение было сравнено с критерием Фишера, вычисленного для вероятности 0.98. При вычислении критерия Фишера были взяты следующие параметры:
Число степеней свободы верхней дисперсии=
число точек в эксперименте- число параметров = 11-4=5;
Число степеней свободы нижней дисперсии=
число точек в эксперименте для определения разброса 10– 1=9.
Доверительная вероятность=0.98.
Число степеней свободы верхней дисперсии=
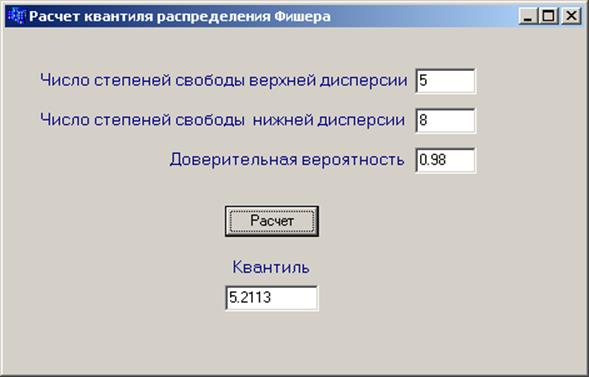
Квантиль=5.2113
Так как отношение дисперсии меньше критерия Фишера, то эти дисперсии статистически неразличимы и модель можно считать адекватной.
В обоих вариантах для параметров функции
заранее известного или предполагаемого вида использовался метод наименьших
квадратов. Параметры функции определяются исходя из условия: сумма квадратов
отклонений между заданными значениями функции ![]() и
полученными в результате аппроксимации с использованием приближающей функции
и
полученными в результате аппроксимации с использованием приближающей функции ![]() в точках
в точках ![]() была бы
минимальной:
была бы
минимальной:
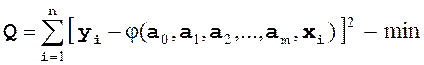 .
.
Параметры ![]() ,
, ![]() , ...,
, ..., ![]() определяются
из системы алгебраических уравнений, которая получается из условия минимума
функции
определяются
из системы алгебраических уравнений, которая получается из условия минимума
функции ![]() :
:
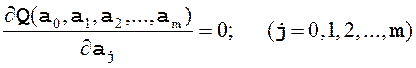 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.