Лабораторная работа №5
Студент: Кохно К.С.
Новосибирск 2010
Теоретические сведения:
Металлургическая граница p-n перехода ![]() в кремниевой структуре с диффузионным
слоем определяется из уравнения:
в кремниевой структуре с диффузионным
слоем определяется из уравнения:
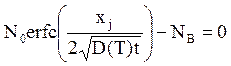 ,
,
где 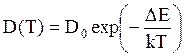
|
Диффузант |
|
|
|
P |
3.85 |
3.66 |
Построить явную
программную модель, описывающую зависимость ![]() .
.
Рассчитать зависимости ![]() или
или ![]() в
диапазонах аргумента и при значениях параметров, указанных в следующей таблице.
в
диапазонах аргумента и при значениях параметров, указанных в следующей таблице.
|
Вариант |
Диффузант |
|
|
|
|
|
5 |
P |
5.1020 |
1.1015 |
900 … 1250 |
75 |
Достроить модель, чтобы она рассчитывала еще и удельное поверхностное сопротивление слоя:
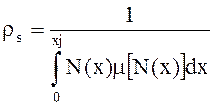 ,
,
где ![]() - эффективная концентрация примеси:
- эффективная концентрация примеси:
![]() ,
,
а ![]() - подвижность основных носителей заряда.
- подвижность основных носителей заряда.
Зависимость ![]() рассчитывать по формуле Зильбергера для Т
= 300 К.
рассчитывать по формуле Зильбергера для Т
= 300 К.
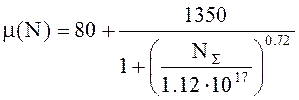 для электронов и
для электронов и
Код программы:
#include <conio.h>
//----------------------------------------------------------------
#include <math.h>
#include <conio.h>
#include <iostream.h>
#include <fstream.h>
#include "root.h"
#include "integral.h"
double F1(double t);
int FxGraph(double(*F)(double),double x1,double x2,int points, char* FileName);
// статические переменные
double _k,_D0,_dE;
// передаваемые переменные
double _N0, _Nb, _T, _t ;
void Constructor();
// вспомогательные функции 1
double erfc(double z);
double D(double T);
double Left1(double x);
// вспомогательные функции 2
double N(double N);
double mu(double N);
double Neff2(double x);
// рабочие функции
double out_Xj (double N0, double Nb, double T, double t, int& err);
double out_ros(double N0, double Nb, double T, double t, double Xj);
//----------------------------------------------------------------
//===========================================================================
void main()
{
// очистка экрана
clrscr();
// внутренние переменные функции
double xj,ros;
int err;
// приводим модель в готовность
Constructor();
// задаем параметры расчета
// выводим Xj
xj=out_Xj(_N0,_Nb,_T,_t,err);
cout<<"err="<<err<<endl;
cout<<"Xj="<<xj<<endl;
// ros
Constructor();
ros=out_ros(_N0,_Nb,_T,_t,xj);
cout<<"ros="<<ros<<endl;
getch();
FxGraph(F1,900,1250,100,"Out1.dat");
}
//===========================================================================
void Constructor()
{
// статические константы
_k = 8.61738E-5;
_D0 = 3.85;
_dE = 3.66;
// глобальные переменные
_N0 = 5E20;
_Nb = 1E15;
_T = 1075;
_t = 75;
}
// ----------------------------------------------------------------------------
double erfc(double z)
{
double t,a;
if (fabs(z)<9.0)
{
t=1/(1+0.3275911*z);
a=t*( 0.254829592+t*(-0.284496736+t*(1.421413741+
t*(-1.453152027+t*1.061405429))));
return a*exp(-z*z);
}
else
return 0.0;
}
// ----------------------------------------------------------------------------
double out_Xj(double N0, double Nb, double T, double t, int& err)
{
err=1;
// внутренние переменные функции
int Nckl;
double F;
double epsX,epsF;
double Xj;
// перенос данных
_N0=N0;
_Nb=Nb; // к-ция доноров
_T=T+273;
_t=t*60.0;
//getch();
// определяем Xj
Xj = 1E-6; // нулевое приближение
epsX = 1E-10; // абс погр выч корня
epsF = 1E4; // абс погр невязки корня с 0
err=RootNewton(Left1,
epsX,epsF,
Xj,F,Nckl,0);
// возвращаем значения в нормальный формат
_t=_t/60.0;
_T=_T-273;
return Xj;
}
// ----------------------------------------------------------------------------
double D(double T)
{ return _D0*exp(-_dE/(_k*T)); }
// ----------------------------------------------------------------------------
double Left1(double x)
{
return (_N0*erfc(x/(2.0*pow(D(_T)*_t,0.5)))-_Nb);
}
// ----------------------------------------------------------------------------
double out_ros(double N0, double Nb, double T, double t, double Xj)
{
// переменные функции
double znam,ros;
// перенос данных
_N0=N0;
_Nb=Nb; // к-ция доноров
_T=T+273;
_t=t*60;
// определяем ROs
znam=SdxSimps(Neff2,0,Xj,100);
ros=1/znam;
// cout<<"ros="<<ros<<endl;
// возвращаем значения в нормальный формат
_t=_t/60.0;
_T=_T-273;
// возвращаем значение
return ros;
}
//============================================================================
double N(double x)
{ return fabs(_N0*erfc(x/(2.0*sqrt(D(_T)*_t)))-_Nb); }
// ----------------------------------------------------------------------------
double mu(double N)
{ return 80+1350/(1+pow((N+2*_Nb)/1.12E17,0.72)); }
// ----------------------------------------------------------------------------
double Neff2(double x)
{
const double q=1.602E-19;
return q*N(x)*mu(N(x));
}
// ----------------------------------------------------------------------------
//============================================================================
double F1(double T)
{
static err;
return out_Xj(_N0,_Nb,T,_t,err);
}
//============================================================================
int FxGraph(double(*F)(double),double x1,double x2,int points, char* FileName)
{
// переменные функции
double dx,FuncValue;
int i;
// открываем файл
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.