Для последующего выполнения сплайн-интерполяции необходимо рассчитать зависимость концентрации электронов и дырок от температуры и концентрации легирующей примеси. В соответствие с заданием на бакалаврскую работу расчетный диапазон температур составлял от 200К до 500К, расчетный диапазон концентрации – от 1015 см-3 до 1020 см-3, причем использовалась логарифмическая шкала концентраций.
Расчет концентрации выполнялся на основе решения уравнения нейтральности относительно уровня Ферми:
, (2.1)
где р - концентрация дырок:
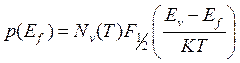(2.2)
n – концентрация электронов:
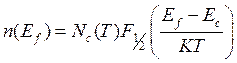(2.3)
Nd+ – концентрация ионизированных акцепторов:
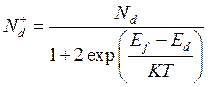(2.4)
Na- - концентрация ионизированных доноров:
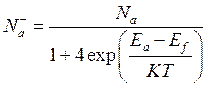(2.5)
Уравнение нейтральности решалась методом половинного деления (бисекции). При решение уравнения были учтены следующие факторы:
1. Квадратичная зависимость ширины запрещенной зоны от температуры:
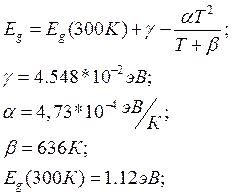(2.6)
2. Зависимость ширины запрещенной зоны и энергий дна зоны проводимости и потолка валентной зоны от степени легирования:
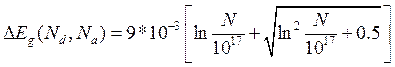, (2.7)
где N – суммарная концентрация легирующей примеси.
При расчете предполагалось, что изменение энергии дна зоны проводимости и потолка валентной зоны происходило пропорционально отношению концентрации:
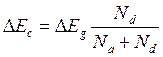(2.8)
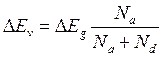(2.9)
Зависимость ширины запрещенной зоны от температуры представлена на рисунке 2.1, а зависимость ширины запрещенной зоны от концентрации степени легирования на рисунке 2.2 (а и б)
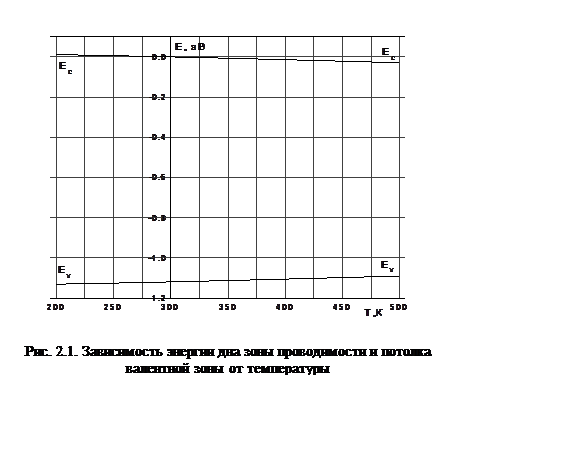
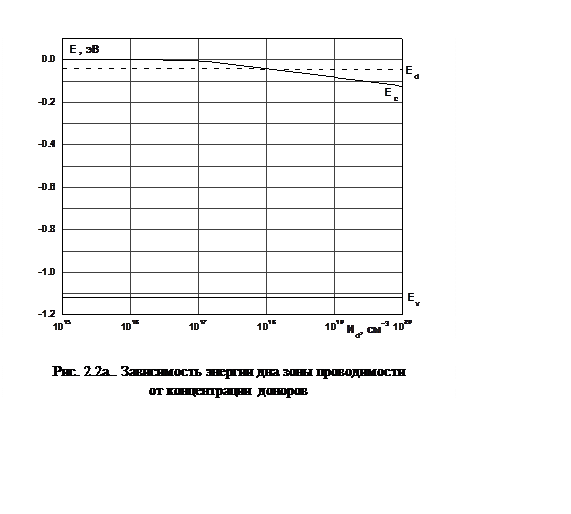
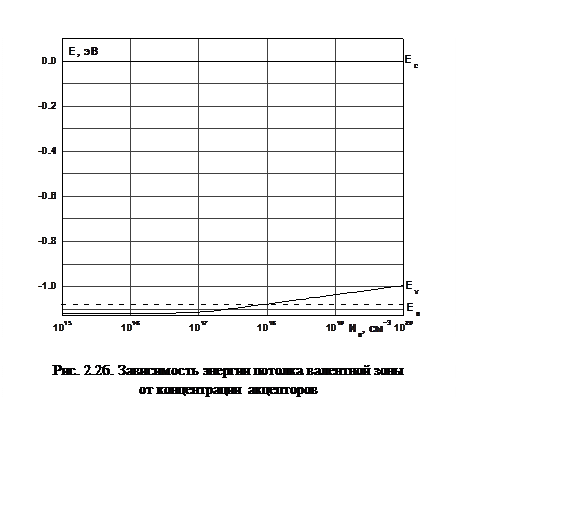
На рис. 2.2 показано, что примесные уровни Ea, Ed, сохраняют постоянные значения и при больших концентрациях заходят в зону проводимости и валентную зону.
На рис. 2.3а представлена зависимость концентрации электронов от температуры для различных концентраций доноров, а на рис. 2.3б – от концентрации доноров при различных температурах.
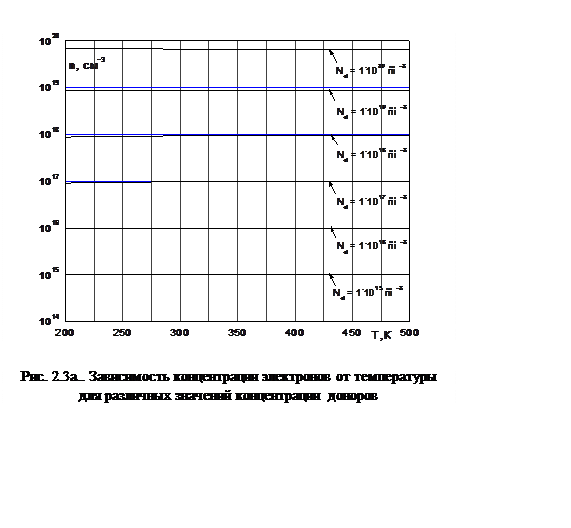
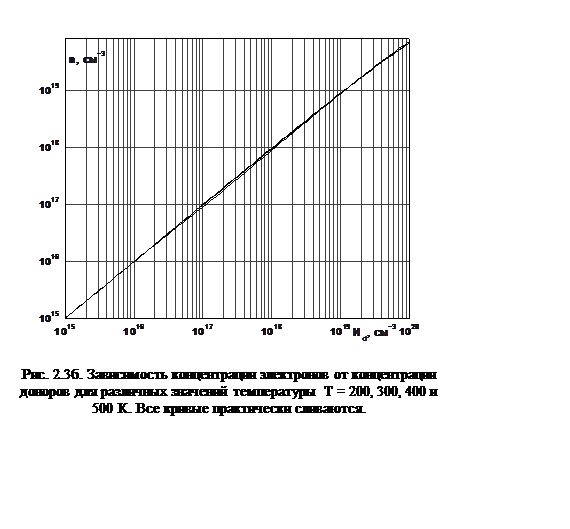
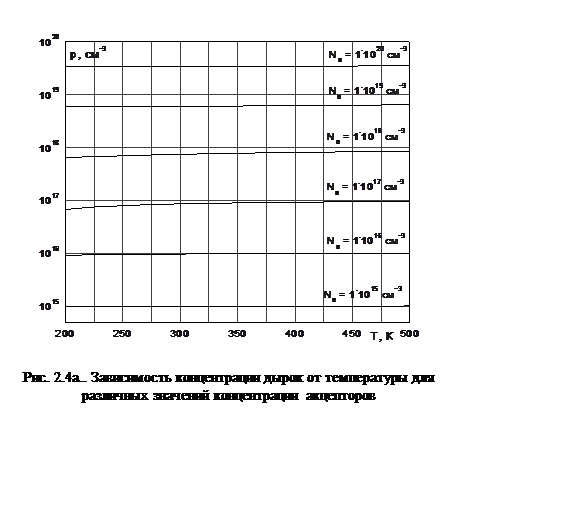
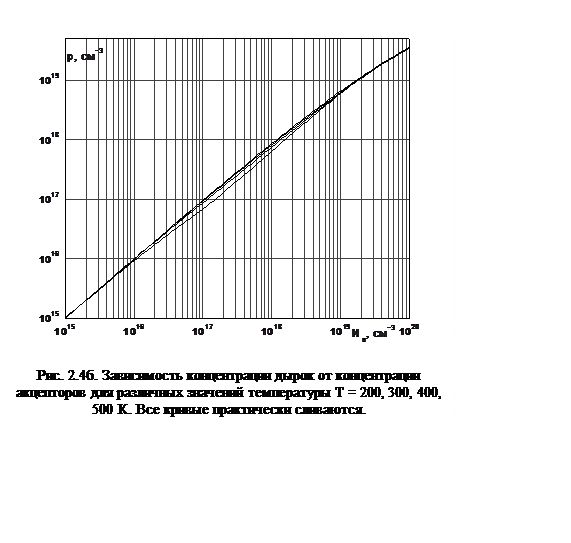
На рис. 2.4 (а и б) показаны аналогичные зависимости для дырок.
Расчет подвижности выполняется с использованием модели Зильбергера, на основе следующих выражений:
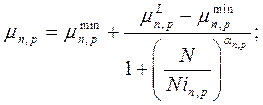(2.10)
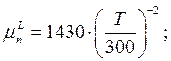
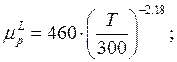
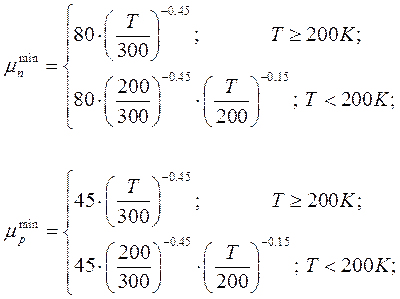
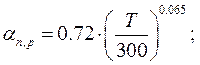
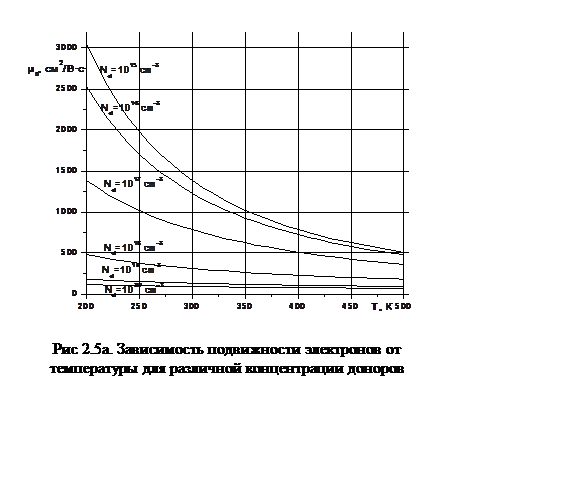
На рис. 2.5а представлена зависимость подвижности электронов от температуры для различных концентраций доноров, а на рис. 2.5б – от концентрации доноров при различных температурах.
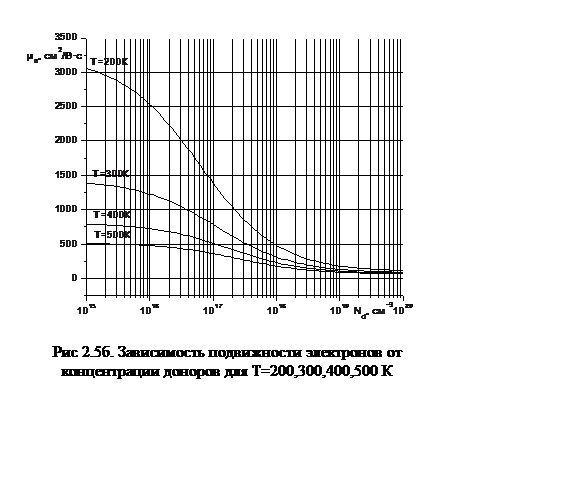
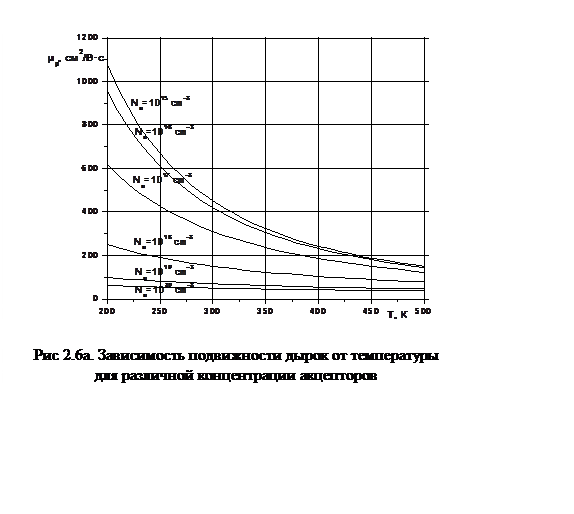
На рис. 2.6 (а и б) показаны аналогичные зависимости для подвижности дырок.
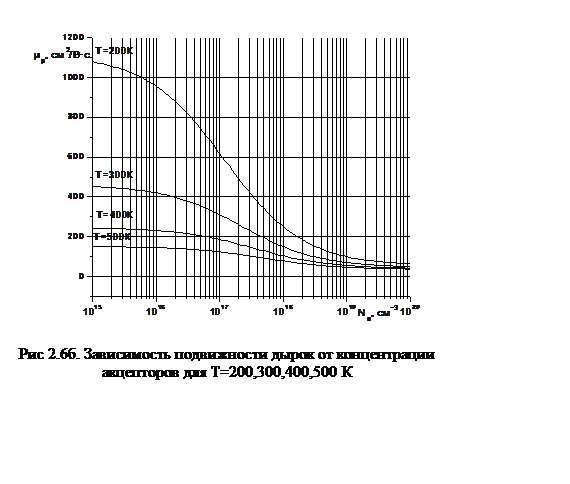
На основе рассчитанных концентраций и подвижностей можно построить графики зависимости удельного сопротивления от температуры и концентрации степени легирования.
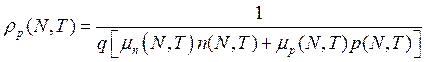(2.11)
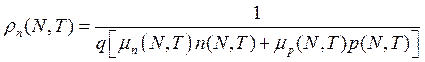(2.12)
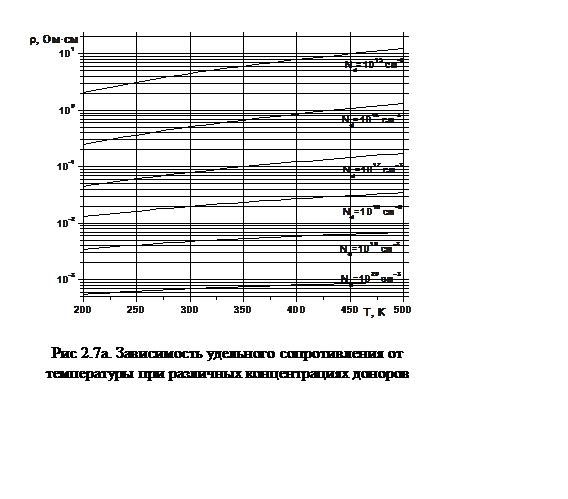
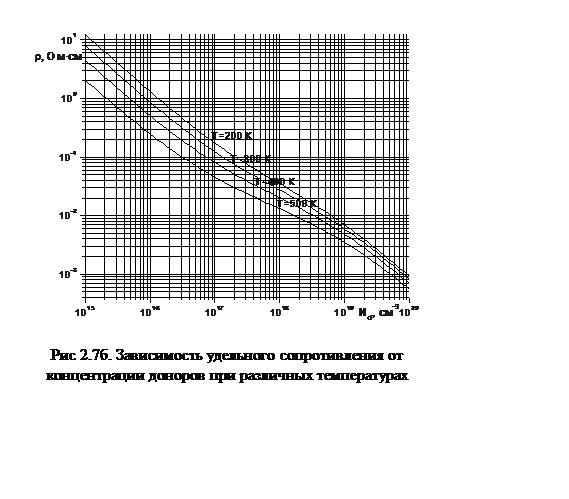
На рис. 2.7а представлена зависимость удельного сопротивления электронов от температуры, а на рис. 2.7б – от концентрации доноров.
На рис. 2.8 (а и б) показаны аналогичные зависимости для удельного сопротивления дырок.
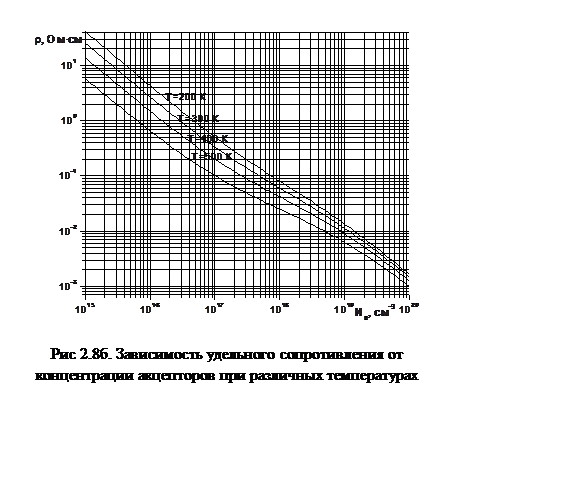
Удельное сопротивление кремния при комнатной температуре 230С может быть вычислено на основе эмпирических формул, приведенных в американском стандарте [12]:
для р – кремния легированного бором:
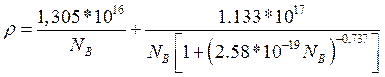(2.13)
для n – кремния легированного фосфором:
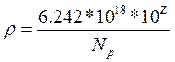
где:
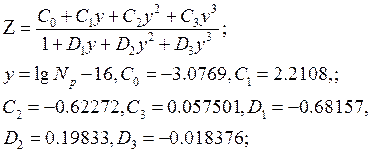(2.14)
- концентрация фосфора в см-3
В результате решений по данным уравнениям были получены расчеты зависимости удельного сопротивления от концентрации легирующей примеси при температуре Т=300К. По этим данным построены графики, которые были сравнимы с графиками, полученными по нашим расчетам. Полученные результаты представлены ниже на рис. 2.9а и 2.9б:
|
|
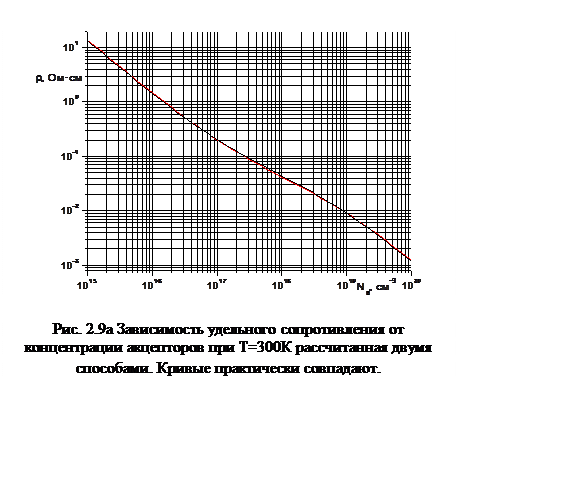
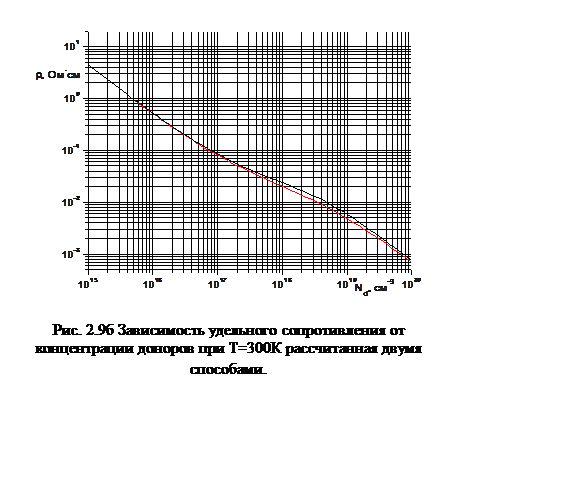
При комнатной температуре графики практически совпадают, на основе чего можно сделать выводы, что и при других температурах они совпадут. Таким образом, наша модель не противоречит американским стандартам и является правильной для расчетов.
Характеристики сенсоров определяются зависимостью от температуры и концентрации, удельного сопротивления и коэффициентов пьезосопротивления. Удельное сопротивление было рассмотрено выше. Необходимо проанализировать и построить модель зависимости коэффициентов пьезосопротивления от температуры и концентрации, так как это важно для практического применения. В литературном обзоре уже упоминалось о неточности результатов, опирающихся лишь на физическую теорию эффекта из-за приблизительных значений параметров. Это приводит к необходимости использовать полуэмпирический метод моделирования, где ряд величин и зависимостей, берутся из экспериментальных данных.
Наиболее детально данный вопрос был рассмотрен Канда[16]. Ниже представлена его модель зависимости коэффициентов пьезосопротивления от температуры и концентрации для n и p – кремния, а также представлены графики, построенные нами по этой модели.
Зависимость коэффициентов пьезосопротивления считается по формуле:
(2.15)
где
является пьезорезистивным фактором и
рассчитывается через интеграл Ферми дробных индексов:
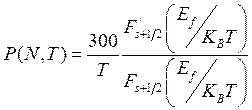(2.16)
В формуле используют не только интеграл Ферми дробных индексов, но и его производную. Интеграл Ферми рассчитывается по формуле:
(2.17)
где s= - 1/2.
Если возьмем от этого интеграла производную и преобразуем ее, то в результате получим:
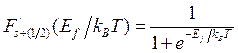(2.18)
В результате вычислений по данным выражениям были получены значения для расчетов зависимости коэффициентов пьезосопротивления от концентрации легирующей примеси в диапазоне температур от – 75 0С до +175 0С.
На рисунке 2.10а представлена зависимость коэффициента пьезосопротивления от примеси доноров при различных температурах, тех же что и в статье Канда.
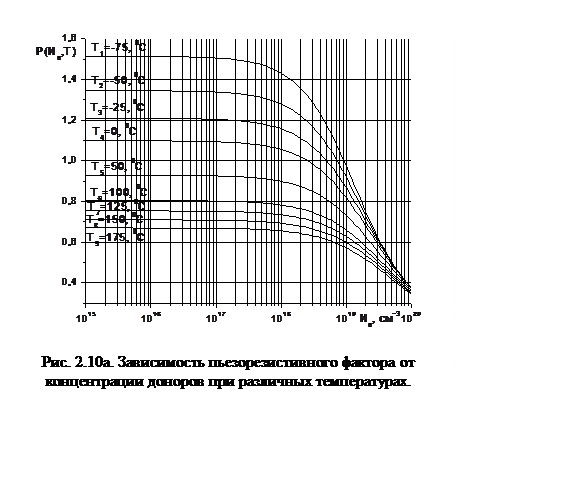
Из рисунка видно, что чем меньше температура, и больше концентрация доноров, тем больше коэффициент пьезосопротивления.
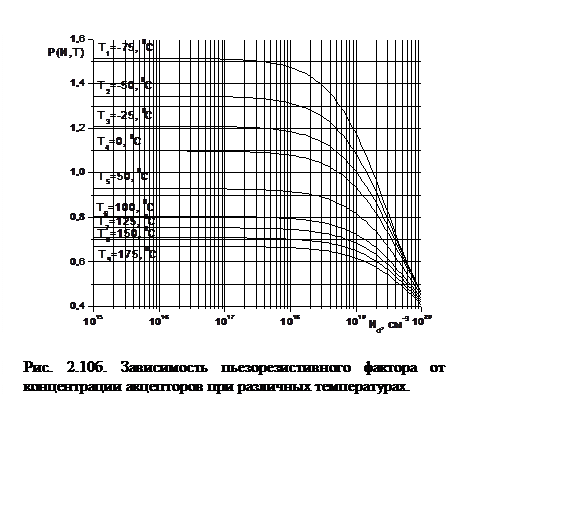
На рисунке 2.10б представлена аналогичная зависимость для концентрации акцепторов при таком же диапазоне температур.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
