Моделирование процесса теплообмена в металлической пластинке.
Исходные данные:
|
Материал пластины |
Условия до начала процесса |
Условия во время процесса |
||
|
T(0), оС |
T(L), оС |
T(0), оС |
T(L), оС |
|
|
Латунь |
150 |
-50 |
50 |
100 |
Материал |
|
|
|
|
Серебро |
8.6 |
0.385 |
111 |
Основным уравнение описывающим процессы теплообмена является уравнение теплопроводности:
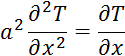
Где:
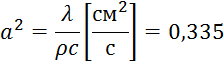
В зависимости от граничных условий решение данного дифференциального уравнения может осуществляться по разному.
1). Граничные условия, когда в момент времени t=0, задана функция.
![]()
![]()
![]()
Область поиска решений разбивается на прямоугольную сетку, получаем n внутренних узлов по координате «x» и неизвестное число внутренних узлов по координате времени, т.к. у нас не ограничено время.
Если рассмотреть ikузел, то можно записать формулы конечных разностей для производных:
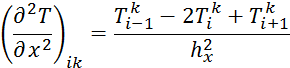
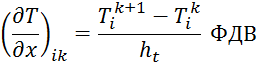
При использовании этих формул получаем:
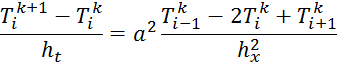
![]()
Индексы
i= (1, 2, ...)
k= (0, 1, 2, ..., n)
На основании этой формулы получаем шаблон численного интегрирования, т.е. по 3-ом точкам определяется значение в 4-ой точке.
При использовании формул дифференцирования назад:
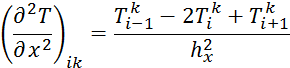
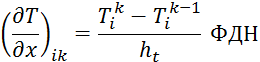
Получаем СЛАУ:
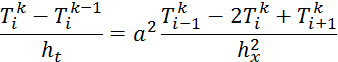
Делая замену по индексам k=k+1, k-1=k, получаем:
![]()
Явный метод (ФДВ) обладает числовой неустойчивостью, в отличие от неявного (ФДН):
![]()
Данный метод обеспечивает точность в пределах 1%.
Выбор шага разбиения сетки осуществляется на основе условия устойчивости:
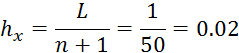
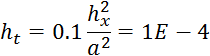
Листинг управляющей программы:
// программа для решения краевой задачи
// с уравнением типа теплопроводности - диффузии
// с помощью TepDif
#include <iostream.h>
#include <conio.h>
#include "tepdif.h"
#include "define.h"
double UL(double);
double UR(double);
double U0(double);
void main()
{
// описание данных
int KeyGr,Nx,Nout,KeyDemo,Ns;
long int Nt;
double a2,L,Ht;
LVector X,T;
vMatrix U;
// ввод входных данных
a2=33.5E-2 ; // параметр уравнения, см^2/c
L=1 ; // толщина пластины, см
KeyGr=1; // ключ левого граничного условия
Nx=49; // число внутренних точек сетки по x
Ht=1E-4 ; // шаг по времени, с
Nt=2000; // число шагов по времени
Nout=100; // число шагов, через которое данные слоя выводятся
KeyDemo=1; // ключ демонстрации хода интегрирования
// расчет
clrscr();
TDExp(UL,UR,U0,a2,L,KeyGr,Nx,Nt,Nout,Ht,KeyDemo, U,X,T,Ns);
// вывод результата
Output(X,T,U,Nx,Ns);
}
double UL(double t)
// левое граничное условие
{
return 50;
}
double UR(double t)
// правое граничное условие
{
return 100;
}
double U0(double x)
// начальное условие
{
return 150-200*x;
}
Полученные результаты:
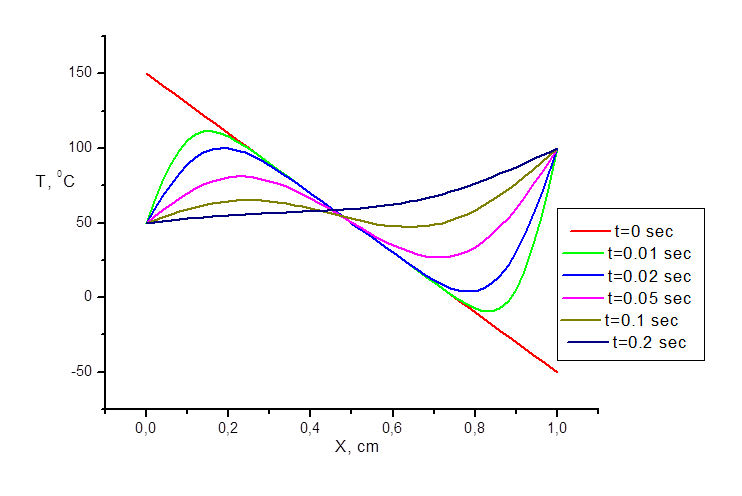
Рисунок 1. Зависимость температуры от координаты при различных значениях времени
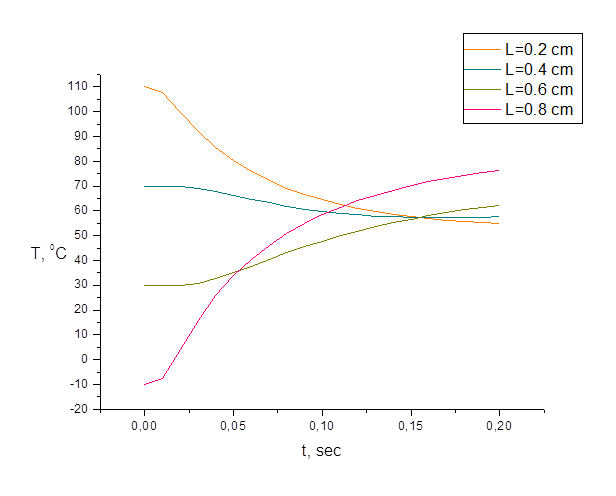
Рисунок 2. Зависимость температуры от времени для различных слоев по координате Х
2). Граничные условия по градиенту.
В качестве граничного условия задается градиент:
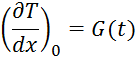
Температура в нулевой точке будет расти, пока не достигнет стационарного состояния.
Рассматриваются так же два случая, аналогичные пункту 1, только с учетом что на левой границе задан градиент изменения температур.
Для явного метода:
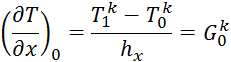
![]()
Листинг управляющей программы:
// программа для решения краевой задачи
// с уравнением типа теплопроводности - диффузии
// с помощью TepDif
#include <iostream.h>
#include <conio.h>
#include "tepdif.h"
#include "define.h"
double UL(double);
double UR(double);
double U0(double);
void main()
{
// описание данных
int KeyGr,Nx,Nout,KeyDemo,Ns;
long int Nt;
double a2,L,Ht;
LVector X,T;
vMatrix U;
// ввод входных данных
a2=33.5E-2 ; // параметр уравнения, см^2/c
L=1 ; // толщина пластины, см
KeyGr=2; // ключ левого граничного условия
Nx=49; // число внутренних точек сетки по x
Ht=1E-4 ; // шаг по времени, с
Nt=2000; // число шагов по времени
Nout=100; // число шагов, через которое данные слоя выводятся
KeyDemo=1; // ключ демонстрации хода интегрирования
// расчет
clrscr();
TDExp(UL,UR,U0,a2,L,KeyGr,Nx,Nt,Nout,Ht,KeyDemo, U,X,T,Ns);
// вывод результата
Output(X,T,U,Nx,Ns);
}
double UL(double t)
// левое граничное условие
{
return -50;
}
double UR(double t)
// правое граничное условие
{
return 100;
}
double U0(double x)
// начальное условие
{
return 150-200*x;
}
Полученные результаты:
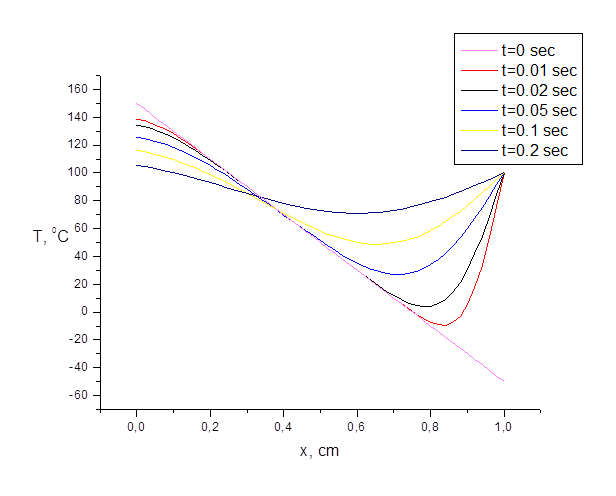
Рисунок 3. Зависимость температуры от координаты при различных значениях времени
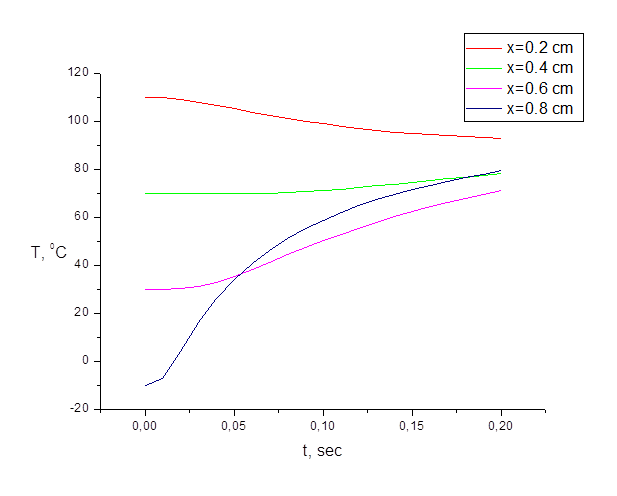
Рисунок 2. Зависимость температуры от времени для различных слоев по координате Х
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.