Вопрос 9. Моделирование упругого элемента в виде консольной балки с помощью пакета программы ANSYS.
Рассмотрим напряженное состояние консольно-защемленной балочки прямоугольного сечения (рис. 1), на свободный конец которой действует сосредоточенная сила. Балочка имеет поперечные размеры a*b, а начало системы координат выбрано в центре свободного конца балочки. Для определенности будем считать, что оси х1, х2, х3 совпадают с главными кристаллографическими осями [100] кремния. Линия действия сосредоточенной силы лежит в плоскостих1ох3.
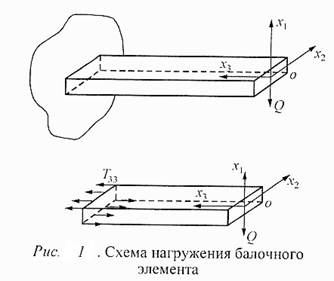
В реальном упругом элементе сосредоточенная сила Qможет действовать на небольшой участок верхней поверхности. Действительное распределение механических напряжений вблизи этого участка неизвестно, поскольку неизвестна форма поверхности контактирующего с балочкой тела. Для упрощения математической формулировки задачи воспользуемся принципом Сен-Венана, который широко применяется при решении задач теории упругости. Этот принцип заключается в следующем. Если на какой-либо площадке δSповерхности тела действует система сил с главным вектором Fи моментом М и в пределах площадки δS происходит перераспределение сил, так что Fи М неизменны, то эти перераспределения не скажутся для точек, удаленных от площадки на расстояние, превышающее ;е максимальный размер.
Принцип Сен-Венана дает определенную свободу в записи граничных условий. Пользуясь этим, предположим, что изгибающая сила Qбалочки приложена к середине ее сечения, х3 =0 . Решения, найденные для такого характера нагружения, будут справедливы для точек балочки х3>b, если b- максимальный размер сечения.
При таком характере нагружения верхние волокна балочки будут растягиваться, а нижние - сжиматься. Учитывая, что толщина а упругих элементов сенсоров много меньше ширины bи длины L, можно считать, что компонента тензора T33 пропорциональна удаленности волокна балочки относительно нейтральной оси, совпадающей с осью х1, т.е:
T33 = Kx1, где К - коэффициент пропорциональности. Его значение можно установить из условия равновесия упругого элемента под действием нагрузки. Для этого сечением х3=свыделим часть упругого элемента справа от сечения, остальную часть балочки мысленно отбросим. Для того чтобы равновесие правой части не нарушалось, действие отброшенной левой части заменим силами, распределенными по сечению х3 =с в соответствии с рис.1, где указаны направления действия компоненты тензора напряжения Т33. Так как «отрезанная» часть упругого элемента находится в равновесии, сумма моментов всех сил относительно оси, проходящей через середину сечения х3 = const параллельно оси х2, должна быть равна нулю
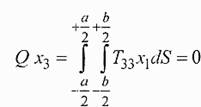
где dS- элемент поверхности сечения х3 =с.
Подставляя вместо Т33 Kx1, находим коэффициент пропорциональности К
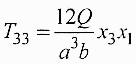 .
.
Для всех точек упругого элемента, кроме торцов балочки, внешние силы отсутствуют (собственным весом балочки по сравнению с силой Qбудем пренебрегать), поэтому для поверхностных точек упругого элемента выполняются равенства
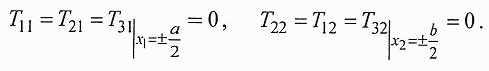
Если деформации волокон балочки невелики, то можно считать, что слои, параллельные боковым граням, не давят друг на друга и не стремятся сдвинуть друг друга. Это позволяет принять для всех точек сечения х=с:
T11 = T12 = T22 = 0.
Вычисления остальных компонент тензора напряжений достаточно трудоемко, но оно облегчаются несколькими обстоятельствами:
- В сенсорах с применением технологии микросистемной техники тензорезистивные слои имеют малую глубину по сравнению с толщиной упругого элемента. Поэтому для всех точек тензорезистивного слоя можно принять, что координата х1«0.5а, т.е. он расположен на поверхности и, как следствие, Т31 << T33. Кроме того, тензорезисторы стремятся разместить в центре балочки, когда х2 = 0, что приводит к равенству Т32 = 0 .
Для узких балочек, когда а>>b, хорошо выполняется соотношение Т31>>Т23. В результате тензор напряжений будет иметь вид:
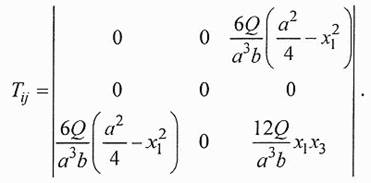
Компоненты тензора деформации волокон балочки можно найти, используя закон Гука:
![]()
Результаты, полученные в ходе моделирования консольной балки в пакете программ ANSYS.
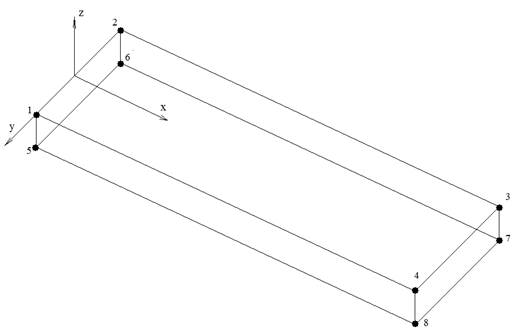
Рис.2. Схема для моделирования консольной балки в ANSYS.
Приведем расчеты для балки в программе модуля consol.
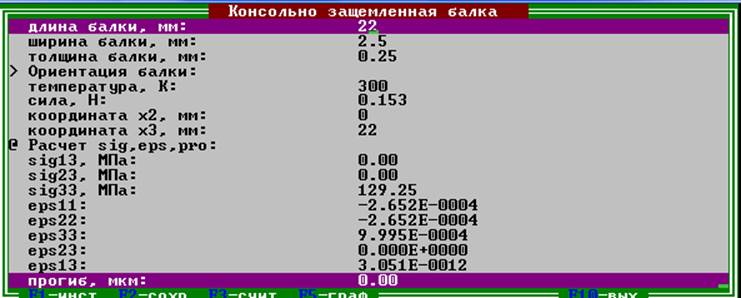
Рис.3. Результаты расчета в программе consol.
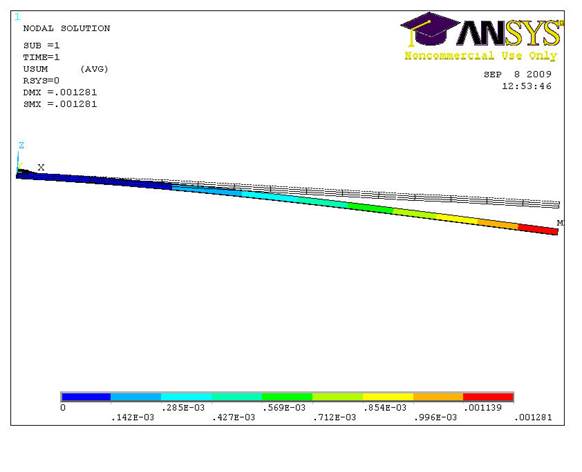
Рис. 4. Деформированная и недеформированная структура балки.
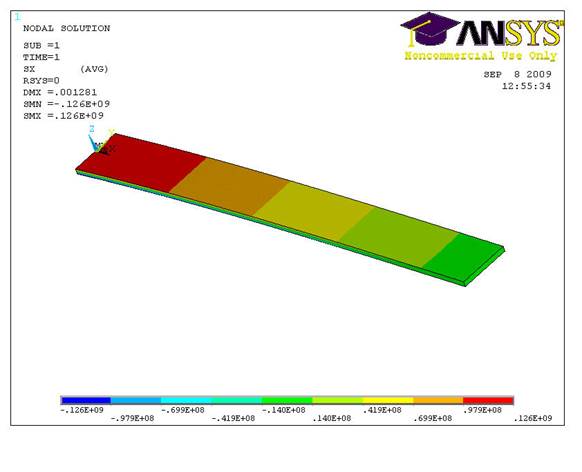
Рис. 5 Распределение напряжений по оси х в консольно-защемленной балке.
Значение максимального напряжения совпадает со значением напряжения полученного в программе consol: 0.126Е+09.
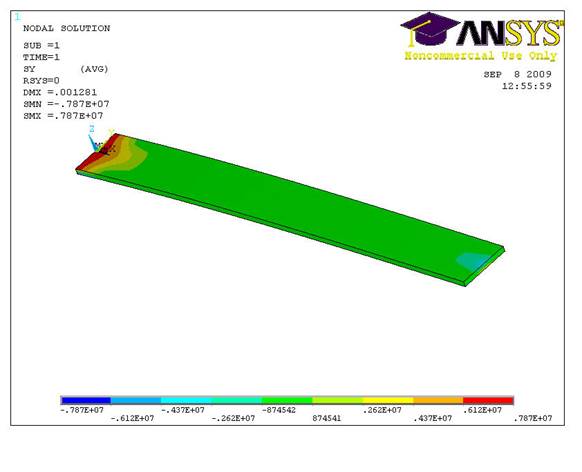
Рис. 6 Распределение напряжений по оси y в консольно-защемленной балке.
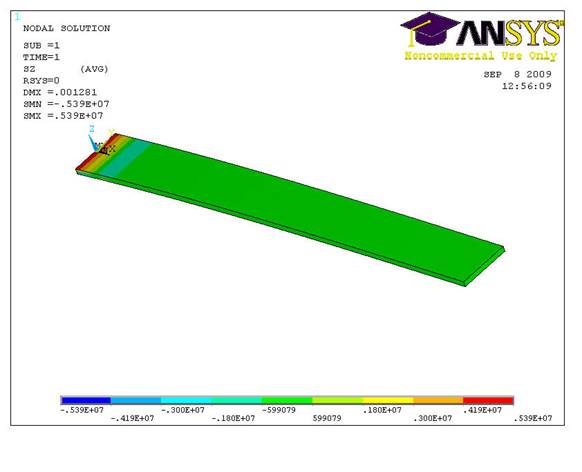
Рис. 7 Распределение напряжений по оси z в консольно-защемленной балке.
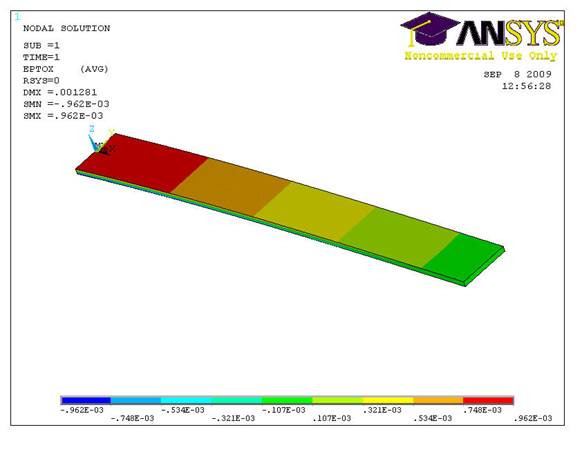
Рис. 8 Распределение деформаций по оси х в консольно-защемленной балке.
Значение максимальной деформации совпадает со значением полученным в программе consol: 0.962Е-03.
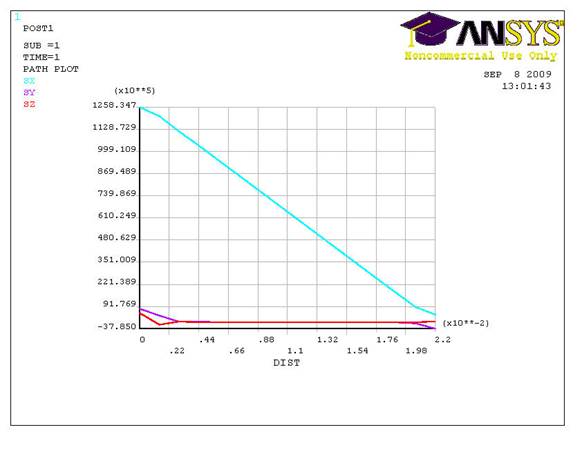
Рис.9. Зависимость напряжений от координаты.
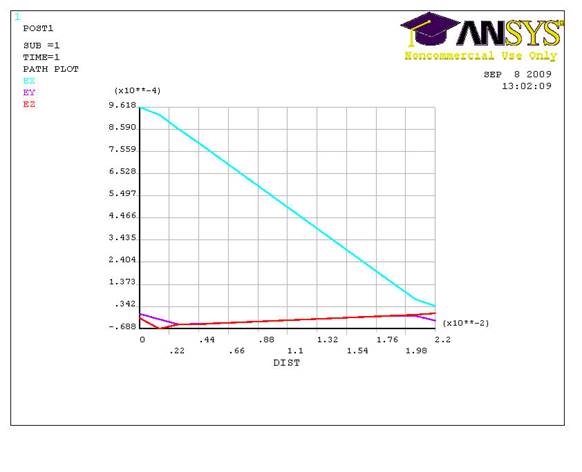
Рис.10. Зависимость деформаций от координаты.
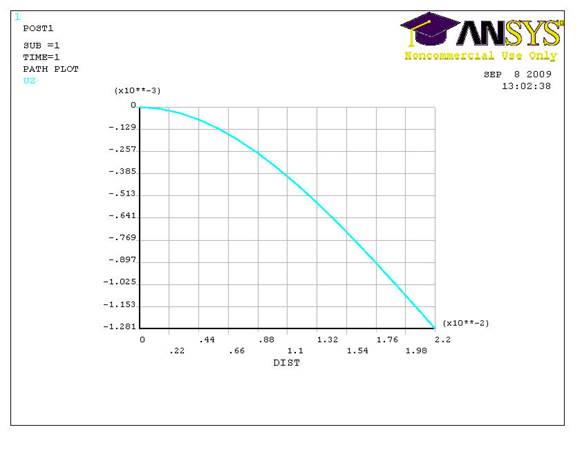
Рис.11. Зависимость прогиба от координаты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.