Моделирование механических напряжений и деформаций круглой и квадратной мембраны. Программы модуля membrana

Вопрос 4. Моделирование механических напряжений и деформаций круглой и квадратной мембраны. Программы модуля membrana.

НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В УПРУГИХ ЭЛЕМЕНТАХ КРУГЛОЙ ФОРМЫ

Круглая форма кремниевых упругих элементов, жестко защемленных по контуру, явилась исторически первой, реализованной в сенсорах давления, созданных с применением микроэлектронной технологии. Необходимость практической реализации жесткого защемления привела к созданию круглых мембран с кольцом жесткости, формируемым различными методами - механической обработкой, зонной плавкой с градиентом температуры, травлением. Профилирование анизотропными травителями стало основной технологией последних двух десятилетий. Этот метод, однако, постепенно вытесняется технологиями сухого травления.

Круглую форму упругих элементов целесообразно применять, когда предъявляются жесткие требования к поперечным размерам сенсоров, например, в медицинской технике в торцевых катетерных сенсорах давлений для инвазивных исследований.

Рассмотрим распределение механических напряжений и деформаций плоской круглой пластины радиуса R, подвергающейся равномерному давлению. Условие жесткого защемления имеет вид:

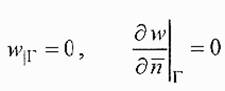
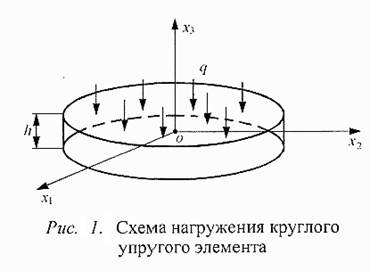
где п - нормаль к контуру пластины Г. Первое из условий означает, что смещение точек контура отсутствует, а второе — что касательные к срединной плоскости или к верхней и нижней поверхностям пластины параллельны координатной плоскости  х₁ох₂ (рис.1).

Для круглой жестко защемленной пластины решение краевой задачи на прогибы имеет вид:

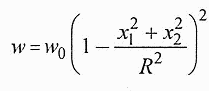
где - wо - прогиб центра круглой пластины. Далее получаем:

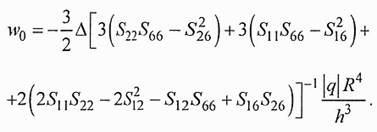
Знак прогиба соответствует направлению приложенной внешней нагрузки в выбранной системе координат.

Исходя из выражения для прогибов wи общих выражений для компонент вектора смещений и тензора деформаций и получаем после некоторых преобразований:

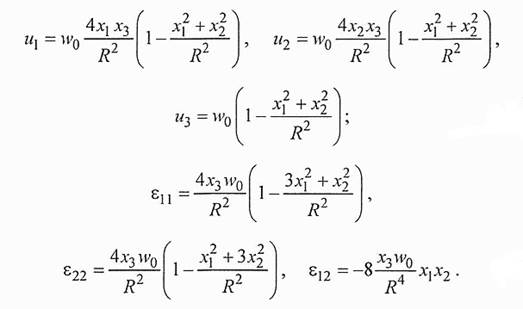
Для описания прогибов и напряжений упругих элементов выберем систему координат в соответствии с ниже приведенной таблицей. Здесь же указаны упругие податливости в выбранной системе координат.

В выбранной системе координат компоненты матрицы упругих податливостей S₁₆, S₂₆равны нулю, что упрощает выражения для прогибов:

.

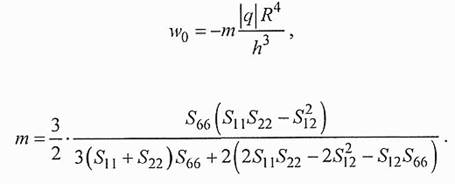Компоненты тензора напряжений и деформаций связаны линейными соотношениями вида:

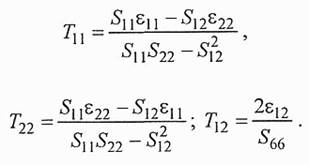
Поскольку глубина тензорезистивных слоев много меньше, чем толщина пластины, наибольший практический интерес имеют напряжения на верхней и нижней поверхностях пластины, когда х₃ = ±hl2 . Учитывая это получаем:

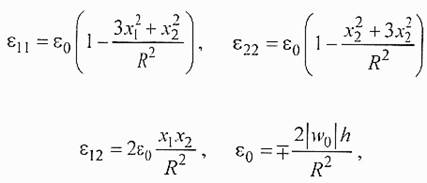
где s₀ - деформация на поверхности в центре пластины. Компоненты тензора напряжений для всех трех плоскостей имеют одинаковую форму:

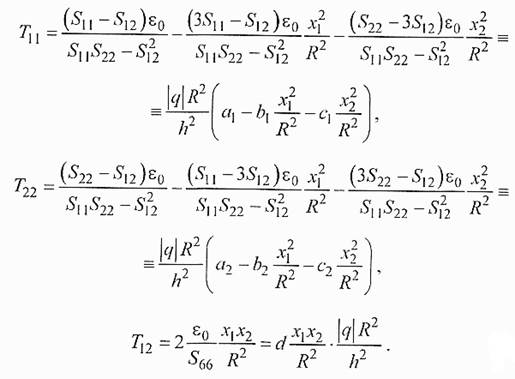
В таблице приведены значения всех постоянных в для рассматриваемых плоскостей:

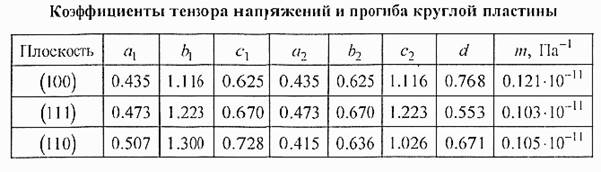
В упругих элементах, плоскость которых совпадает с кристаллографической плоскостью (100)  или  (111), податливости  S₁₁и S₂₂равны, что дополнительно упрощает выражения для компонент тензора напряжений Т₁₁ и Т₂₂. Для компоненты Т₁₁  получаем:

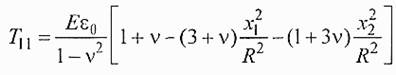
здесь учтено, что Е = 1 /S_l1, - модуль Юнга и v = -S_l2 /S₁₁- коэффициент Пуассона.

В кремнии плоскость (111) является плоскостью упругой изотропии, для которой выполняются соотношения а₁=а₂, b₁=с₂, c₁=b₂. Это еще более упрощает выражения для нормальных компонент тензора напряжении T₁₁ и T₂₂ (x₃=h/2):

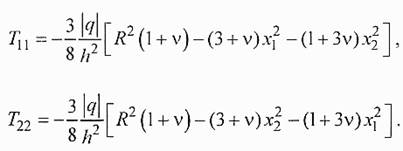
МЕХАНИЧЕСКИЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В КВАДРАТНОЙ ЖЕСТКОЗАЩЕМЛЕННОЙ ПЛАСТИНЕ.

В настоящее время широкое распространение получили упругие элементы, центральная часть которых представляет квадратную или прямоугольную тонкую пластинку постоянной толщины, находящуюся в условиях жесткого защемления. При измерении давления на такую пластинку действует равномерно распределенная нагрузка интенсивностью q . Расчет напряжений и деформаций сводится к решению уравнения на прогибы  w(x_lx₂)  пластины с соответствующими граничными условиями:

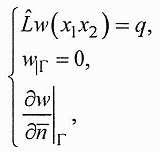
где оператор Lопределен в общем виде выражением (2.8.11), Г -контур пластины ий- нормаль к контуру. Решение задачи (3.2.1), которое описывает поведение пластины при малых прогибах, может быть проведено различными методами, в частности:

1) интегрированием с применением двойных рядов Фурье. Сходимость рядов при этом оказывается не очень быстрой и требуется большой объем вычислений;

2) применением методов конечных разностей и конечных элементов. Решение возможно лишь с применением ЭВМ и соответствующих пакетов программ, например ANSYS, и требует большого объема вычислительной работы;

3) использованием вариационных принципов механики.

Вариационные методы решения чрезвычайно удобны для микросистемной техники, поскольку позволяют получить результаты в аналитической форме и с приемлемой для техники точностью. Существует несколько модификаций вариационных методов решения: энергетический, метод Галеркина - Ритца, комбинированный метод Л.В. Конторовича, метод обращения, эффективность применения, которых зависит от конкретной формулировки задачи.

Для случаев малых прогибов квадратных и прямоугольных упругих элементов весьма эффективен метод Галеркина - Ритца, суть которого состоит в следующем.

Задавая виртуальный прогиб точек пластины δw(x_xx₂), можно вычислить работу нагрузки qлибо непосредственно из интеграла:

либо косвенно, используя вырахение:

Если w - точное решение, то выше приведенные интегралы должны совпадать, как это следует из дифференциального уравнения краевой задачи. Поскольку точное решение неизвестно, его можно представить приближенно в виде ряда:

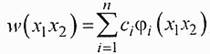
Тип функций φ_i можно выбрать, ориентируясь на ожидаемую форму прогибов упругого элемента, а число членов ряда - разумным компромиссом между объемом вычислений и точностью получаемых результатов.

Коэффициенты с_i определим из условия минимума интеграла:

который по структуре соответствует формулировке принципа Ла-гранжа.

Варьируя поочередно коэффициенты с_i в, получаем набор вариаций прогибов

Далее получаем систему уравнений для определения коэффициентов с_i:

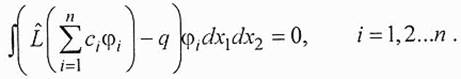
Численные расчеты напряжений и деформаций будем далее приводить для трех основных кристаллографических ориентации плоскости упругого элемента - (100), (110), (111).

Ориентацию сторон пластины выберем в соответствии с таблицей. Систему координат свяжем со срединной плоскостью, а начало координат поместим в центр пластины (рис.2).

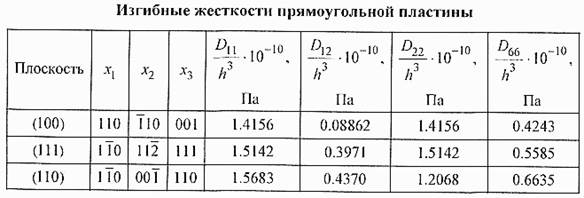
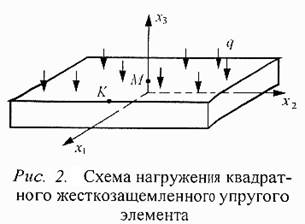
В выбранной системе координат пластины обладают ортотропной упругой симметрией и компоненты матрицы упругих податливостей S₁₆ и S₂₆ равны нулю. В этом случае oператор L принимает вид:

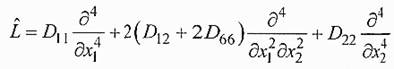
здесь Dij- изгибные жесткости анизотропной пластины, выражающиеся через упругие податливости кремния в системе координат, связанной со сторонами пластины:

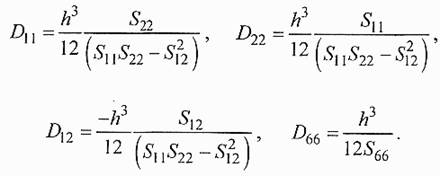
Граничные условия  применительно к рассматриваемому случаю имеют вид:

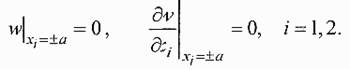
Для квадратной пластины прогибы будем искать в виде:

Компоненты тензора деформаций и напряжений определяются общими соотношениями (ля удобства расчетов приведем выражения компонент тензора напряжений через прогибы):

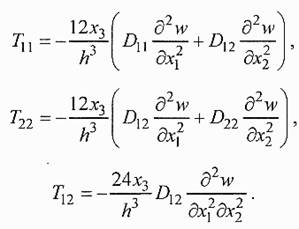
Толщины тензорезистивного слоя много меньше толщины пластины, так что для проектирования сенсоров давления можно принять координату х₃ = ±h/2 . В этом случае, компоненты Т₁₃ = Т₂₃ = 0.

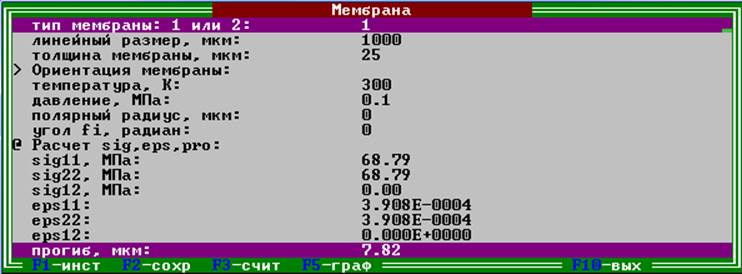
Scaner1

Scanner 2

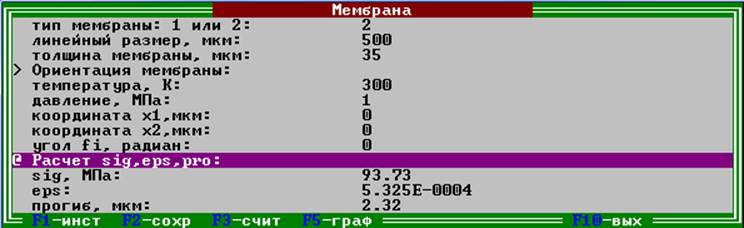
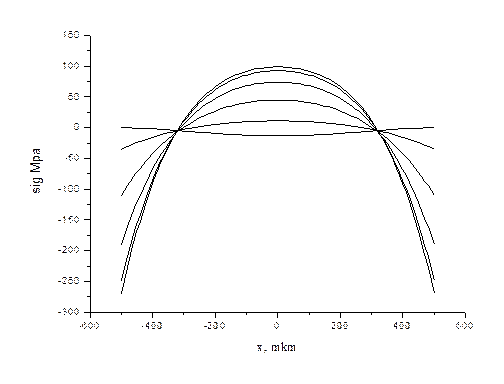
Рис.3. Зависимость напряжения sig₃₃ от координаты x₁ при различных x₂