Лабораторная работа №1
Решение СЛАУ
Студент Кохно
Группа РМС7-71
Преподаватель Лобач
Задача 2
2. Выполнить процесс решения СЛАУ, заданной преподавателем, двумя методами – Гаусса и LU-разложения (с выводом промежуточных данных в файлы). Проанализировать ход решения и сравнить с описанием алгоритмов.
Текст программы (метод Гаусса):
// Программа для решения СЛАУ с помощью LinGauss или LinDecomp и LinSolve
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A,L,U;
Vector B,X;
// задание входных данных
keyDemo=3;
n=4;
A[1][1]= 2.2; A[1][2]= 3.1; A[1][3]= 1.1; A[1][4]=-1.2;
A[2][1]= 0.3; A[2][2]= 1.7; A[2][3]= 2.9; A[2][4]=-0.5;
A[3][1]= 3.1; A[3][2]= 0.1; A[3][3]=-5.1; A[3][4]= 2.1;
A[4][1]=-3.0; A[4][2]= 2.5; A[4][3]= 1.6; A[4][4]= 8.1;
B[1]= 6.9; B[2]= 10.4; B[3]=-3.6; B[4]=39.2;
// решение СЛАУ
Err1=LinGauss(n,A,B,X,keyDemo);
// Err1=LinDecomp(n,A,L,U,keyDemo);
// Err2=LinSolve(n,L,U,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
}
Пример работы программы в файле LINGAUSS.DAT
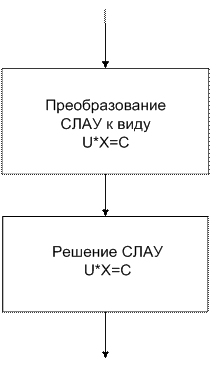
Блок-схема:
![]() - исходная система.
- исходная система.
Метод Гаусса основан на замене исходной системы на
эквивалентную (т.е. имеющую то же решение ![]() ), но с
матрицей
), но с
матрицей ![]() верхней треугольной формы:
верхней треугольной формы:
![]()
Матрица ![]() получается путем
преобразования исходной матрицы
получается путем
преобразования исходной матрицы ![]() , а вектор
, а вектор ![]() - из вектора
- из вектора ![]() . Так
как матрица
. Так
как матрица ![]() - треугольная, все компоненты вектора
- треугольная, все компоненты вектора ![]() , начиная с
, начиная с ![]() , легко
находятся последовательно.
, легко
находятся последовательно.
Алгоритм метода Гаусса состоит из двух этапов:
Преобразование ![]() и
и ![]() . - прямой ход;
. - прямой ход;
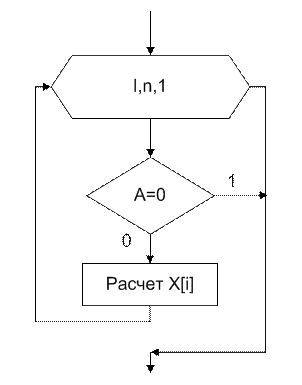
Последовательное вычисление ![]()
![]() – обратный ход.
– обратный ход.
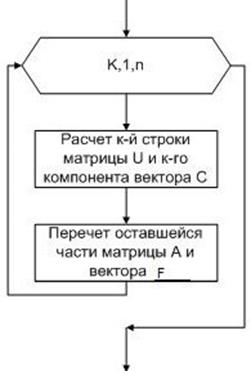
Прямой ход Обратный
ход
Текст программы (метод LU-разложения):
// Программа для решения СЛАУ с помощью LinGauss или LinDecomp и LinSolve
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A,L,U;
Vector B,X;
// задание входных данных
keyDemo=3;
n=4;
A[1][1]= 2.2; A[1][2]= 3.1; A[1][3]= 1.1; A[1][4]=-1.2;
A[2][1]= 0.3; A[2][2]= 1.7; A[2][3]= 2.9; A[2][4]=-0.5;
A[3][1]= 3.1; A[3][2]= 0.1; A[3][3]=-5.1; A[3][4]= 2.1;
A[4][1]=-3.0; A[4][2]= 2.5; A[4][3]= 1.6; A[4][4]= 8.1;
B[1]= 6.9; B[2]= 10.4; B[3]=-3.6; B[4]=39.2;
// решение СЛАУ
// Err1=LinGauss(n,A,B,X,keyDemo);
Err1=LinDecomp(n,A,L,U,keyDemo);
Err2=LinSolve(n,L,U,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
}
Пример работы программы в файле LINLU.DAT
i Sum X[i]
4 0.00 4.00
3 4.20 3.00
2 5.41 2.00
1 2.14 1.00
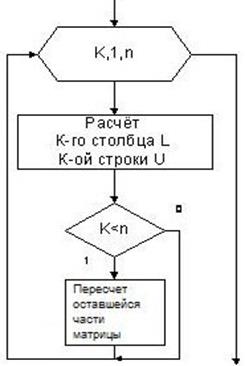
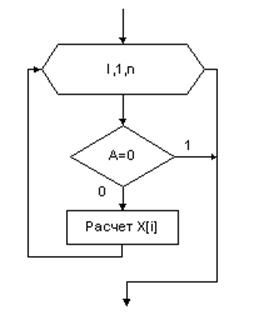
Блок-схема:
Метод LU-разложения основан на том, что матрица ![]() может быть представлена в виде
произведения двух матриц:
может быть представлена в виде
произведения двух матриц:
![]() где
где ![]() - нижняя треугольная
матрица,
- нижняя треугольная
матрица,
![]() - верхняя треугольная матрица с
единичной главной диагональю.
- верхняя треугольная матрица с
единичной главной диагональю.
При этом разложении исходная система разлагается на две, но с треугольными матрицами:

![]()
![]() которые легко решаются последовательно, т.е. сначала из
решения системы находится вектор промежуточных неизвестных
которые легко решаются последовательно, т.е. сначала из
решения системы находится вектор промежуточных неизвестных ![]() , а затем, используя найденный вектор
, а затем, используя найденный вектор ![]() в качестве вектора свободных членов,
решается система и находится искомый вектор неизвестных
в качестве вектора свободных членов,
решается система и находится искомый вектор неизвестных ![]() .
.
Прямой ход Обратный ход

Задача 3
3. Методами Гаусса и LU-разложения выполнить решение СЛАУ
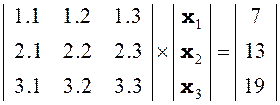 , которая имеет решением значения
, которая имеет решением значения ![]() ,
, ![]() и
и ![]() , в чем легко убедиться умножением
матрицы на этот вектор. Объяснить полученный результат.
, в чем легко убедиться умножением
матрицы на этот вектор. Объяснить полученный результат.
Текст программы (метод Гаусса):
// Программа для решения СЛАУ с помощью LinGauss или LinDecomp и LinSolve
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A,L,U;
Vector B,X;
// задание входных данных
keyDemo=3;
n=3;
A[1][1]= 1.1; A[1][2]= 1.2; A[1][3]= 1.3;
A[2][1]= 2.1; A[2][2]= 2.2; A[2][3]= 2.3;
A[3][1]= 3.1; A[3][2]= 3.2; A[3][3]= 3.3;
B[1]=7; B[2]=13; B[3]=19;
// решение СЛАУ
Err1=LinGauss(n,A,B,X,keyDemo);
// Err1=LinDecomp(n,A,L,U,keyDemo);
// Err2=LinSolve(n,L,U,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
}
Пример исполнения(метод LU-разложения):
Err1 = 0
Err2 = 0
Vector X:
2.000 4.000 0.000
Текст программы(метод гауса):
// Программа для решения СЛАУ с помощью LinGauss или LinDecomp и LinSolve
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
#include "matrix.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A,L,U;
Vector B,X,N,Y;
// задание входных данных
keyDemo=3;
n=3;
A[1][1]= 1.1; A[1][2]= 1.2; A[1][3]= 1.3;
A[2][1]= 2.1; A[2][2]= 2.2; A[2][3]= 2.3;
A[3][1]= 3.1; A[3][2]= 3.2; A[3][3]= 3.3;
B[1]=7; B[2]=13; B[3]=19;
N[1]=3; N[2]=2; N[3]=1;
// решение СЛАУ
Err1=LinGauss(n,A,B,X,keyDemo);
// Err1=LinDecomp(n,A,L,U,keyDemo);
// Err2=LinSolve(n,L,U,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
LinMxV(n,A,N,Y);
cout<<"Vector B:"<<endl;
printf("%6.3f %6.3f %6.3f",Y[1],Y[2],Y[3]);
getch();
}
Пример исполнения:
Err1 = 0
Err2 = 0
Vector X:
4.000 0.000 2.000
Vector B:
7.000 13.000 19.000
Вывод: решением данной матрицы являются несколько векторов. Это объясняется тем, что эта матрица вырожденная (ее определитель равен нулю) значит данная СЛАУ имеет бесконечное множество решений.
Задача 4
4. Выполнить решение СЛАУ из п. 2 с выводом промежуточных результатов с помощью функций LinGaussPro() или LinDecompPro() и LinSolvePro() (по указанию преподавателя). Проанализировать ход решения и сравнить с описанием алгоритмов.
Текст программы:
// Программа для решения СЛАУ с помощью LinGaussPro
// или LinDecompPro и LinSolvePro
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A;
Vector B,X;
iVector P;
// задание входных данных
keyDemo=3;
n=4;
A[1][1]= 2.2; A[1][2]= 3.1; A[1][3]= 1.1; A[1][4]=-1.2;
A[2][1]= 0.3; A[2][2]= 1.7; A[2][3]= 2.9; A[2][4]=-0.5;
A[3][1]= 3.1; A[3][2]= 0.1; A[3][3]=-5.1; A[3][4]= 2.1;
A[4][1]=-3.0; A[4][2]= 2.5; A[4][3]= 1.6; A[4][4]= 8.1;
B[1]=6.9; B[2]=10.4; B[3]=-3.6; B[4]=39.2;
// решение СЛАУ
Err1=LinGaussPro(n,A,B,X,keyDemo);
// Err1=LinDecompPro(n,A,P,keyDemo);
// Err2=LinSolvePro(n,A,P,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
}
Пример исполнения: см. файл 4LINGAUSS.DAT
i Sum X[i]
4 0.00 4.00
3 4.20 3.00
2 5.41 2.00
1 2.14 1.00
Задача 5
5. Методом прогонки выполнить решение СЛАУ, имеющей трехдиагональную матрицу, (заданной преподавателем) с выводом промежуточных данных в файл. Проанализировать ход решения и сравнить с описанием алгоритмов.
Текст программы:
// Программа для решения СЛАУ методом прогонки
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,n,keyDemo,Err;
double Rmod;
Matrix A;
Vector R,P,Q,F,X,RR;
// задание входных данных
n=5;
P[1]=1; Q[1]=3; F[1]=7;
R[2]=2; P[2]=1; Q[2]=4; F[2]=16;
R[3]=2; P[3]=-1; Q[3]=2; F[3]=9;
R[4]=4; P[4]=1; Q[4]=2; F[4]=26;
R[5]=3; P[5]=1; F[5]=17;
keyDemo=3;
// решение
Err=LinProgon(n,R,P,Q,F,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err = "<<Err<<endl;
cout<<endl;
cout<<"Вектор X: ";
for (i=1; i<=n; i++)
printf("%7.3f ",X[i]);
cout<<endl;
getch();
Пример исполнения: 5LINPROGO.DAT
i Sum X[i]
4 0.00 4.00
3 -6.74 3.00
2 1.12 2.00
1 -2.16 1.00
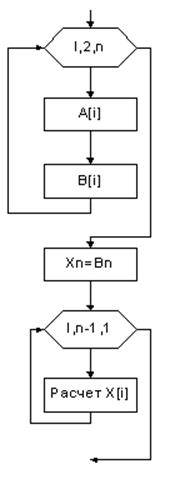
Блок-схема:
Метод прогонки применяется для СЛАУ с трехдиагональной матрицей, в которой все элементы, не входящие в главную и прилегающие к ней диагонали, равны нулю:
![]()
коэффициенты СЛАУ хранятся и обрабатываются в виде трех одномерных массивов: ![]() -
массива элементов главной диагонали,
-
массива элементов главной диагонали, ![]() - массива элементов
ниже главной диагонали и
- массива элементов
ниже главной диагонали и ![]() - массива элементов
выше главной диагонали. Индекс элемента массивов
- массива элементов
выше главной диагонали. Индекс элемента массивов ![]() ,
, ![]() или
или ![]() соответствует
индексу строки матрицы.
соответствует
индексу строки матрицы.
Идея метода прогонки основана на представлении каждой компоненты вектора неизвестных через следующую:
![]()
где ![]() и
и ![]() - прогоночные коэффициенты, которые
необходимо определить.
- прогоночные коэффициенты, которые
необходимо определить.

Задача 6
6. Выполнить решение системы из п. 5 с помощью метода Гаусса или LU-разложения (по указанию преподавателя).
Текст программы:
// Программа для решения СЛАУ с помощью LinGauss или LinDecomp и LinSolve
#include <iostream.h>
#include <stdio.h>
#include <conio.h>
#include "linsys.h"
void main()
{
// описание данных
int i,j,n,keyDemo,Err1=0,Err2=0;
Matrix A,L,U;
Vector B,X;
// задание входных данных
keyDemo=3;
n=5;
A[1][1]= 1; A[1][2]= 3; A[1][3]= 0; A[1][4]= 0; A[1][5]= 0;
A[2][1]= 2; A[2][2]= 1; A[2][3]= 4; A[2][4]= 0; A[2][5]= 0;
A[3][1]= 0; A[3][2]= 2; A[3][3]=-1; A[3][4]= 2; A[3][5]= 0;
A[4][1]= 0; A[4][2]= 0; A[4][3]= 4; A[4][4]= 1; A[4][5]= 2;
A[5][1]= 0; A[5][2]= 0; A[5][3]= 0; A[5][4]= 3; A[5][5]= 1;
B[1]=7; B[2]=16; B[3]=9; B[4]=26; B[5]=17;
// решение СЛАУ
// Err1=LinGauss(n,A,B,X,keyDemo);
Err1=LinDecomp(n,A,L,U,keyDemo);
Err2=LinSolve(n,L,U,B,X,keyDemo);
// вывод результата
clrscr();
cout<<"Err1 = "<<Err1<<endl;
cout<<"Err2 = "<<Err2<<endl;
cout<<endl;
cout<<"Vector X:"<<endl;
for (i=1; i<=n; i++)
printf("%6.3f ",X[i]);
cout<<endl;
getch();
}
Пример исполнения: файл 6LINLU.DAT
i Sum X[i]
4 0.00 4.00
3 4.20 3.00
2 5.41 2.00
1 2.14 1.00
Задача 7
7. Используя программу из файла cond.exe, рассчитать числа обусловленности матриц СЛАУ, решаемых при выполнении предыдущих пунктов задания. Сделать вывод о влиянии числа обусловленности на точность решения СЛАУ.
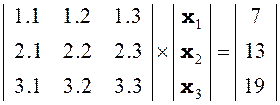 Число обусловленности cond=1.626744e+17
Число обусловленности cond=1.626744e+17
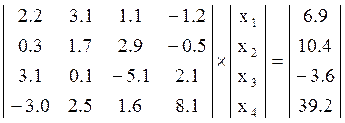 Число
обусловленности cond = 16.573734
Число
обусловленности cond = 16.573734
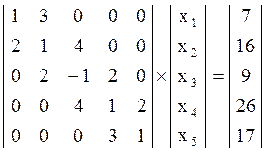 Число
обусловленности cond =
18.175613
Число
обусловленности cond =
18.175613
Вывод: Чем больше значение числа обусловленности, тем больше погрешность вычисления вектора неизвестных.
Задача 8
8. Проверить работу одной из функций (по указанию преподавателя
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.