 Раздельное наблюдение двух линий с наименьшим интервалом
dλ длин волн определяется разрешающей способностью линзы.
Разрешающая способность линзы зависит от дифракционных явлений на краях призмы,
т.е. от ее размеров, а также от дисперсии материала призмы. Согласно расчетам,
спектральная призма дает для каждой спектральной линии определенный дифракционный
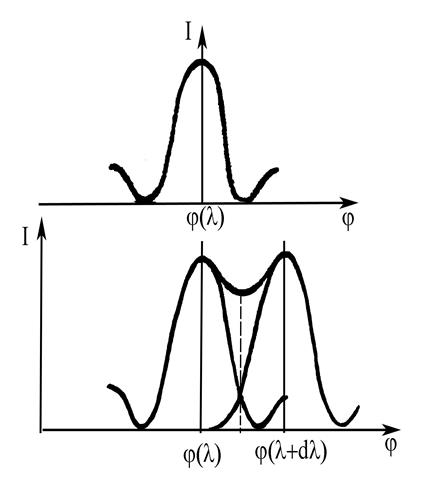
инструментальный контур, показанный на рисунке 2. Две близкие спектральные линии
дадут суммарный инструментальный контур (I – величина,
пропорциональная освещенности; φ – угол (направление на линию спектра)).
Раздельное наблюдение двух линий с наименьшим интервалом
dλ длин волн определяется разрешающей способностью линзы.
Разрешающая способность линзы зависит от дифракционных явлений на краях призмы,
т.е. от ее размеров, а также от дисперсии материала призмы. Согласно расчетам,
спектральная призма дает для каждой спектральной линии определенный дифракционный
инструментальный контур, показанный на рисунке 2. Две близкие спектральные линии
дадут суммарный инструментальный контур (I – величина,
пропорциональная освещенности; φ – угол (направление на линию спектра)).
Разрешающая сила оптического аппарата должна отвечать критерию Рэлея, согласно которому наименьший разрешимый интервал dλ равен расстоянию между главным максимумом и первым минимумом функции, описывающей инструментальный контур. Если две линии, имеющий одинаковый инструментальны контур, расположены таким образом, что максимум контура совпадает с первым минимум другой, то они будут разрешимы, т.е. видны отдельно. При этом ордината минимума суммарной кривой равна ~80% от максимума.
В случае одной призмы разрешающая способность 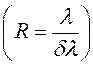 выражается формуле
выражается формуле 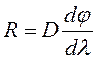 ,
где D – ширина параллельного пучка, выходящего из призмы;
,
где D – ширина параллельного пучка, выходящего из призмы; ![]() - угловая дисперсия призмы.
- угловая дисперсия призмы.
Экспериментальная часть
Задачей настоящей работы является построение градуировочного графика монохроматора УМ-2 и определение его дисперсионных характеристик.
Принципиальная схема спектрального аппарата представлена на рисунке 3 и состоит из трех основных частей: коллиматора (2-5) – устройства, формирующего узкий параллельный пучок лучей; дисперсирующей призмы (призмы 6 или дифракционная решетка), разлагающей немонохроматический свет в спектр, и зрительной трубы (7-10) для наблюдения и регистрирования спектра. Свет от источника 1 проходит через конденсатор 2 – короткофокусная линза (или система линз), используемая для концентрации светового потока и равномерного освещения поля изображения, линзу 3 и освещает щель 4, которая расположена в фокальной плоскости объектива коллиматора 5. Образовавшийся параллельный пучок лучей попадает на диспергирующую систему призм 6. Вследствие дисперсии (n=n(λ)) лучи с различными длинами волн выйдут под разными углами – произойдет пространственное разделение спектра. Объектив зрительной трубы 7 выходная щель 8 выделяет лучи почти параллельные оси выходной трубы. Регистрация спектра производится через окуляр 9.
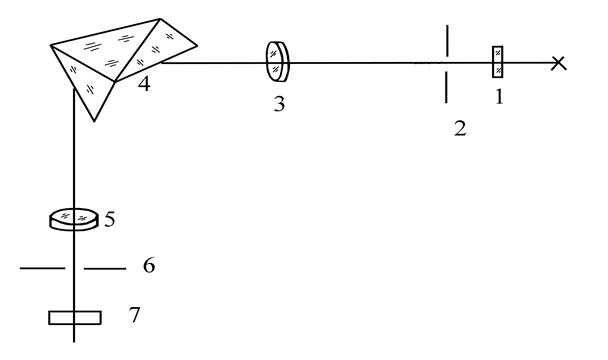 |
5 – объективы; 4 – призма; 6 – выходная щель
Рисунок 6 - Оптическая схема УМ-2
Основными характеристиками спектрального аппарата
являются угловая и линейные дисперсии. Угловая дисперсия β зависит
только от диспергирующего элемента аппарата. Линейная дисперсия L
определяется, кроме того, геометрическими условиями фокусировки спектра. Если
угловому расстоянию dφ соответствует
линейное расстояние dS в плоскости изображения объектива зрительной трубы
прибора, то линейная дисперсия 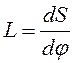 . По величине угловой
дисперсии нетрудно получить значение линейной дисперсии L.
Действительно, если расстояние между двумя спектральными линиями, отличающееся
по длине волны на dλ, равно dS, то это расстояние при
малых углах связано с углом dφ равенством
. По величине угловой
дисперсии нетрудно получить значение линейной дисперсии L.
Действительно, если расстояние между двумя спектральными линиями, отличающееся
по длине волны на dλ, равно dS, то это расстояние при
малых углах связано с углом dφ равенством
![]() , где
, где ![]() -
фокусное расстояние объектива зрительной трубы, отсюда получим
-
фокусное расстояние объектива зрительной трубы, отсюда получим 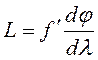 , но
, но 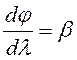 , отсюда
, отсюда
![]() . Обычно линейная дисперсия выражается в
миллиметрах на нанометр (мм/нм).
. Обычно линейная дисперсия выражается в
миллиметрах на нанометр (мм/нм).
В данной работе предлагается определить линейную дисперсию спектрального аппарата – монохроматора УМ-2 во всем диапазоне видимого спектра и найти графический закон изменения дисперсии с длиной волны.
Наблюдение спектральных линий и измерение из положения производится на монохроматоре УМ-2 со стеклянной оптикой. Внешний вид монохроматора и инструкция по эксплуатации представлены на стенде в лаборатории.
Приборы и принадлежности
Монохроматор УМ-2, ртутная лампа, блок питания.
Порядок выполнения работы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.