Спектральный анализ в физике конденсированного состояния: Лабораторный практикум, страница 4

2.  Булатов М.И. Калинкин И.П. Практическое руководство по фотоколориметрическим и спектрометрическим методам анализа. – Л.: Химия, 1979. – 376с.

Лабораторная работа №2 ОС

Изучение спектрального аппарата УМ-2

Краткая теория

1. Зависимость показателя преломления от частоты (цвета) называется дисперсией. Следствием этого является разложение пучка белого света при прохождении его сквозь призму, а также расплывание импульсов, различие фазовой и групповой скоростей, неравномерное движение волновых фронтов и т.д.

Согласно классическим представлениям электроны атомов совершают вынужденные колебания под действием электрического поля световой волны с частотой, равной частоте приходящей волны. В результате этого колеблющиеся электроны сами излучают добавочную волну. Суммарное поле складывается из поля падающей и добавочной волны. Количественный анализ указанной ситуации позволяет прийти к зависимости [1]

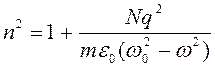, где N – концентрация атомов;

            ε₀ – диэлектрическая постоянная;

q, m – заряд и масса электрона.

2. Рассмотрим роль призмы как дисперсирующиго элемента.

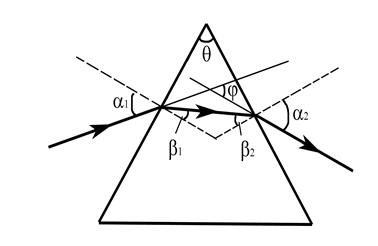Призма для спектрального разложения была впервые использована Ньютоном. Простейшей спектральной призмой является призма треугольного сечения с параллельными ребрами, выполненная из прозрачного материала и обладающая значительной дисперсией  (рисунок 1).

При прохождении через призму пучок лучей в результате двукратного преломления отклоняется на некоторый угол φ по отношению к падающему лучу. Так как показатель преломления материала призмы зависит от длины волны λ, то при прохождении естественного света через призму углы отклонения φ оказываются различными для различных длин волн λ, и, следовательно, осуществляется пространственное разложение излучения по длинам волн.

Найдем зависимость приращения угла выхода луча из призмы dφ при изменении длины волны от λ до λ+dλ, т.е. выражение для угловой дисперсии. Из геометрических соображений угол наклона луча

                         (β₁+β₂=θ)                  (1)

Из (1) следует, что φ зависит от n  только благодаря α₂, т.к. α₁ определяется углом поворота призмы относительно оси коллиматора, а θ определяется инструментальным параметром призмы. Для того, чтобы выразить угловую дисперсию призмы 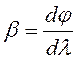, достаточно выразить α₂ через n  и α₁. Используя законы преломления

       ;                                    (2)

и соотношение  , получим:

   .                               (3)

Продифференцируем (1) по λ и, используя (3), получим:

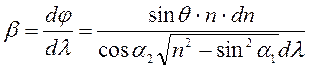         .                                (4)

Так как в зависимости (4) , где sinα₂, в свою очередь, выражается через α₁ и n (см. (3)), то угловая дисперсия β зависит только от величины дисперсии , угла падения света на призму α₁ и показателя преломления n.

3. Главным элементом любого спектрального анализа является дисперсирующая (dispersio – рассеяние) система, разлагающая произвольное излучение на сумму монохроматических длин волн.

В спектральном аппарате УМ-2 в качестве дисперсирующей системы используется призма Аббе. Это так называемая система постоянного отклонения. Главной особенностью призмы Аббе является то, что для луча, выходящего из призмы под углом α₂=α₁, выполняется условие φ=90⁰. Если для какой-либо длины волны λ₂ φ(λ₂)=90⁰, то для λ₁<λ₂ имеем φ(λ₁)<90⁰, а для λ₃>λ₁ φ(λ₃)<90⁰. Поэтому в фокусе выходной трубы будет наблюдаться линия, соответствующая только длине волны λ₂, а линии, соответствующие длинам волн λ₁ и λ₃, наблюдаться не будут. Поэтому вращение призмы приводит к сканированию спектра. Наличие значительной угловой дисперсии еще не обеспечивает возможности раздельного наблюдения двух близких спектральных линий λ и λ'.