Подводный старт межконтинентальной баллистической ракеты из затопленной шахты с помощью ЖРД при наличии воздушного колокола, страница 14

                    Графическое представление результатов расчета
                                 для базового варианта 1

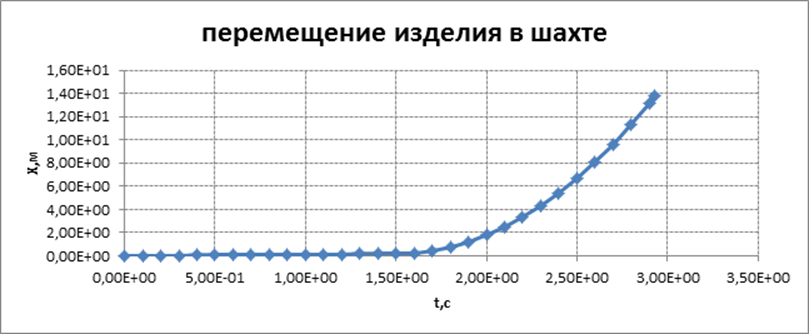
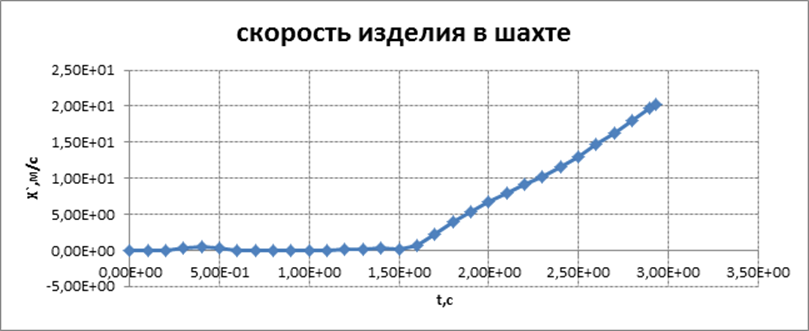
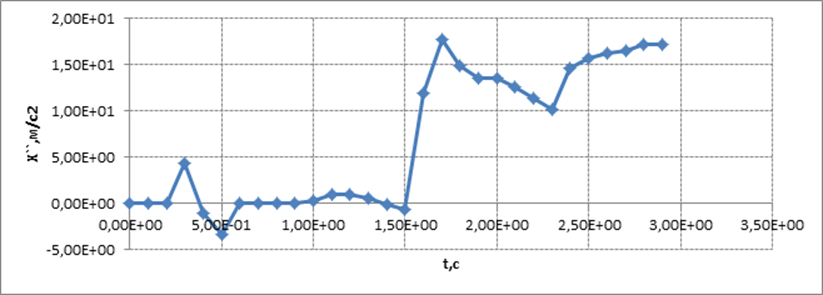
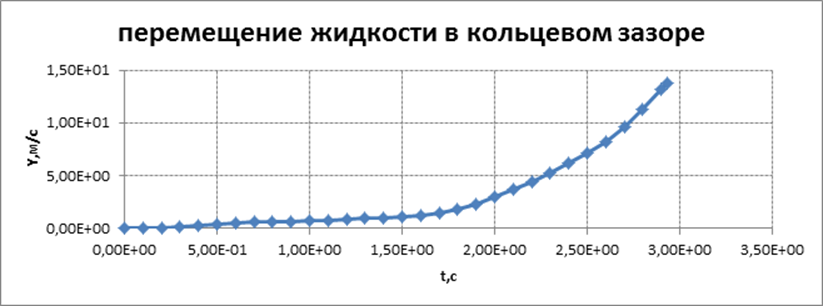
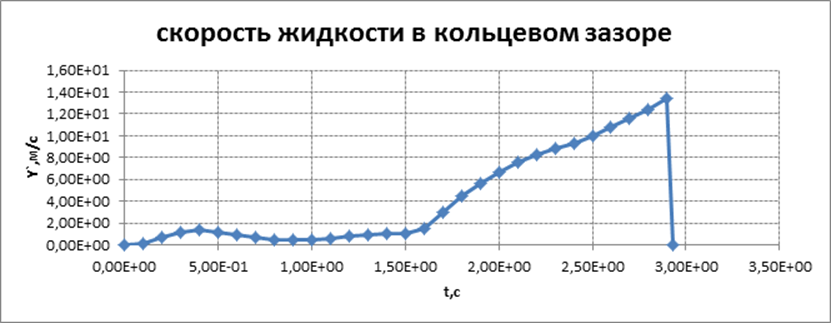
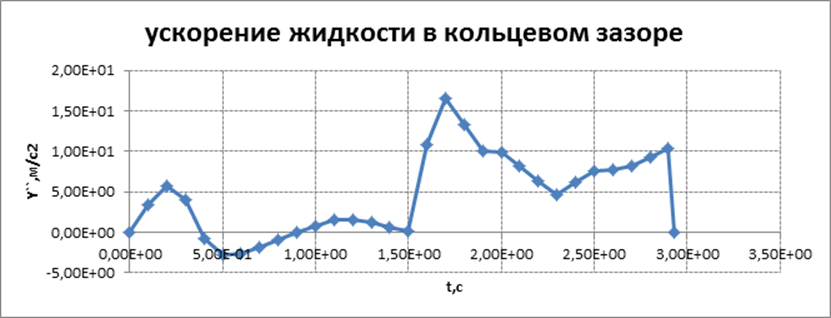
 Циклограмма запуска двигательной установки первой ступени МБР

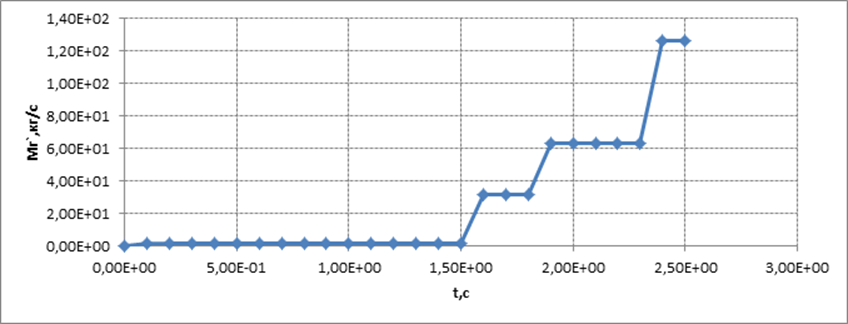
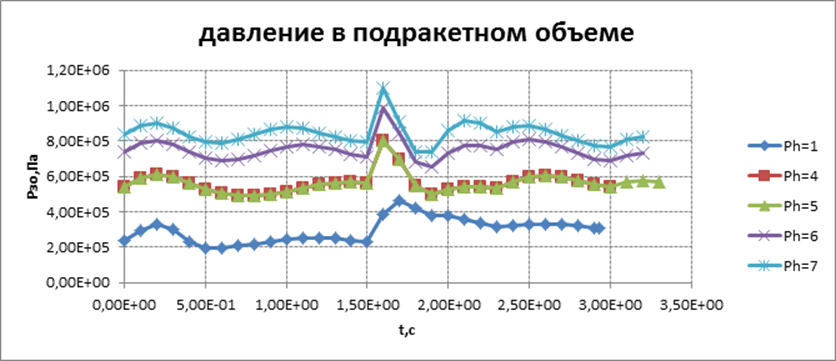
            Графическое представление результатов расчета для всех вариантов

.

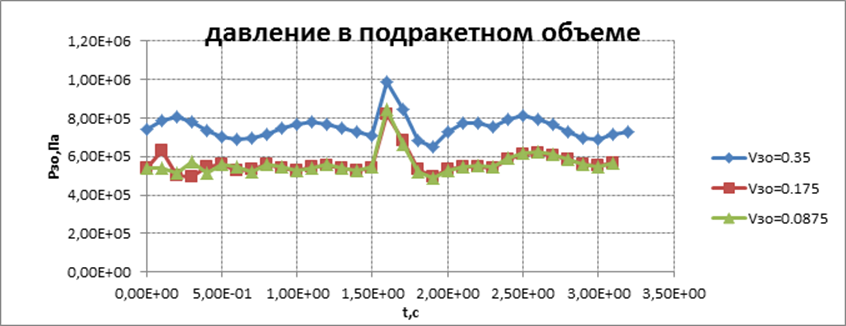
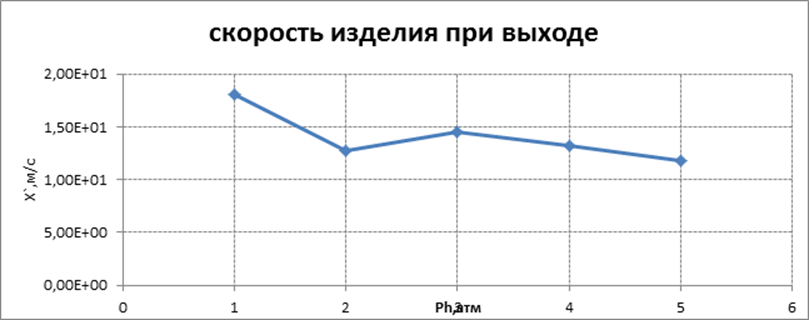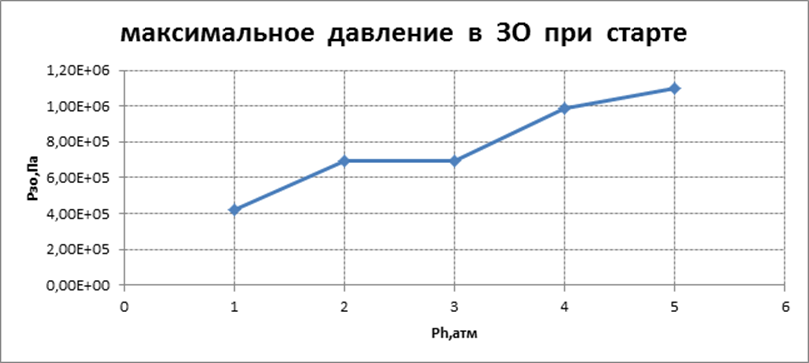
4. Определение параметров старта изделия с помощью ПАД.

Рассматривается схема подводного старта МБР из обтюрированной ПУ с помощью ПАД (рис. 4.1).

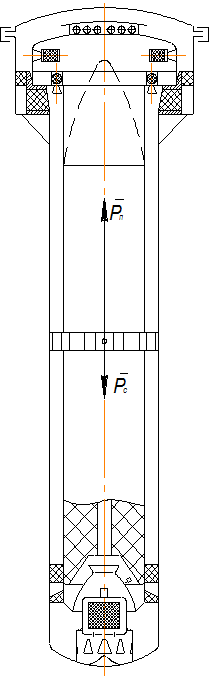
Рисунок 4.1 Схема старта изделия из обтюрированной ПУ с помощью ПАД.

Математическая модель процесса старта изделия с помощью ПАД.

Допущения:

1.  Изделие абсолютно твердое тело, движение изделия одномерное;

2.  Рабочие газы в подракетном объеме подчиняются уравнению состояния идеальных газов;

3.  Потери в рабочих объемах (КС и ЗО) учитываются интегральными коэффициентами теплопотерь: ,   ;

4.  Влиянием ударно-волновых процессов на параметры движения изделия пренебрегаем;

Система уравнений.

1.  Уравнение скорости горения твердого топлива.

-  степенной закон скорости горения:

,

-  линейный закон скорости горения:

,

где   ,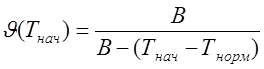

           - начальная температура твердого топлива;

           - температура при нормальных атмосферных условиях(288К);

           - термохимическая константа.

2.  Расход газов из КС.

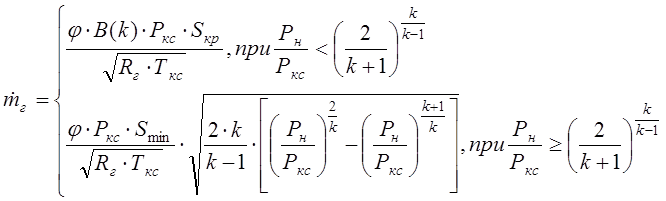
где 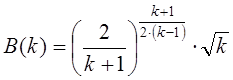,   при .

3.  Уравнение прихода газов в КС.

,

4.  Уравнение массового прихода газа при горении топлива.

,

5.  Уравнение изменения температуры в КС (из уравнения энергии):

,

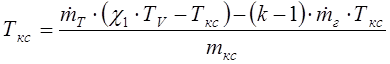6.  Уравнение изменения давления (из уравнения состояния газа):

,

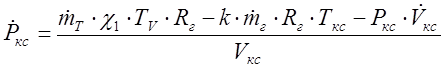7.  Уравнение изменения объема КС.

,

Уравнения 1 –7 служат для внутрибаллистического расчета ПАД.

8.  Уравнение изменения температуры в подракетном объеме.

,

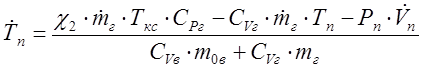9.  Уравнение изменения давления в подракетном объеме.

,

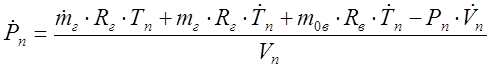10.  Уравнение изменения подракетного объема.

,

11.  Уравнение движения ракеты в ПУ.

,

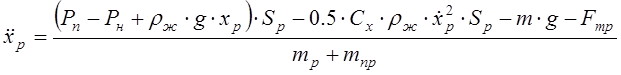где     .

Полученная система дифференциальных уравнений второго порядка приводится к системе уравнений первого порядка путем замены:

,

,

.

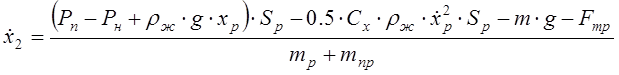Система дифференциальных уравнений первого порядка решается методом Рунге-Кутта четвертого порядка точности при начальных условиях:

Начальные условия при :

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.

Результаты расчета.

Расчет выполнялся с помощью компьютерной программы «BS». В результате было рассчитано два варианта:

1. с увеличенной в 1.5 раза по сравнению с первой л/р массой ракеты;

2. с увеличенной на 20% массой полученной для первого варианта.

Вариант 1

BR_DAT  Выполнил Шумков А.Ю.         группы a461
Данные по вкладышу АД
плот.= 1650 кг/м3, п.адиаб.= 1.200 , газ.const= 320.0 Дж/кг/К, Tp= 2600 К
коэф.расх.= 0.970 , коэф.потерь= 0.950 , ТЕТА= 1.000 , Pzag=  2000000 Па
Законы скорости горения
ст. 1: от Р=   200000 Па до Р= 40000000 Па u0= 1.700 ню= 0.500
ст. 2: от Р=        1 Па до Р=        2 Па u0= 0.200 ню= 0.200
лин.1: от Р=        1 Па до Р=        2 Па  a= 1.000  b= 0.0100
Геометрия вкладыша и активные поверхности
r0= 0.0110 м, l= 0.370  м, n=  37 шт., rN= 0.1000 м, rM= 0.0000 м
zM= 0 , zT= 0 , zrN= 0 , zr0= 1
Начальные условия в КС
пл.крит.= 0.0089000 м2, св.объем=  0.012000 м3, Р=  2000000 Па, Т= 1600 К
max шаг= 0.0001 с, огранич.по времени-  2.500 с, относит.погр.= 0.00100
вывод: на экран- 0.0500 с, в файл1- 0.0500 с, в файл2- 0.0500 с
BS_DAT   Данные по изделию, ПУ и среде:
масса изделия  63000.0 кг, его диаметр 2.200 м, путь 16.000 м,              !!!!!
коэф.трения 0.100, коэф.лоб.сопр. 0.250, прис.масса  1260.0 кг,
плотн.среды 1000.00 кг/м3, давлен.среды   400000 ПА, коэф.т.п. 0.800,
нач.объем  1.730 м3, нач.давление    98100 Па, нач.темпер.  290 °К,
угол возвышения 90.0°,
площ.зазора 0.000000 м2, коэф.расх. 0.950, переп.раскрытия   200000 Па