Подводный старт межконтинентальной баллистической ракеты из затопленной шахты с помощью ЖРД при наличии воздушного колокола

Балтийский  государственный технический

университет “ВОЕНМЕХ” 

им. Д.Ф. Устинова

Кафедра A4

Лабораторные работы

 по курсу: проектирование стартовых комплексов морского базирования (СК МБ)

1.  Определение параметров старта МБР с ЖРД.

2.  Определение потерь тяги ЖРД под водой.

3.  Численное моделирование процессов старта МБР с ЖРД с учетом потерь тяги.

4.  Определение параметров старта изделия с помощью ПАД.

5.  Анализ схем КПУ.

                 6.Отработка заряда ПАД при переменной внешней нагрузке.

	Выполнил:
	Шумков А.Ю.
	студент группы А-461
	Проверил:
	Молчанов И. Н.

Санкт-Петербург 2010  г.

1. Определение параметров старта МБР с ЖРД.

Рассматривается подводный старт МБР из затопленной шахты с помощью ЖРД при наличии воздушного колокола (рис. 1.1).

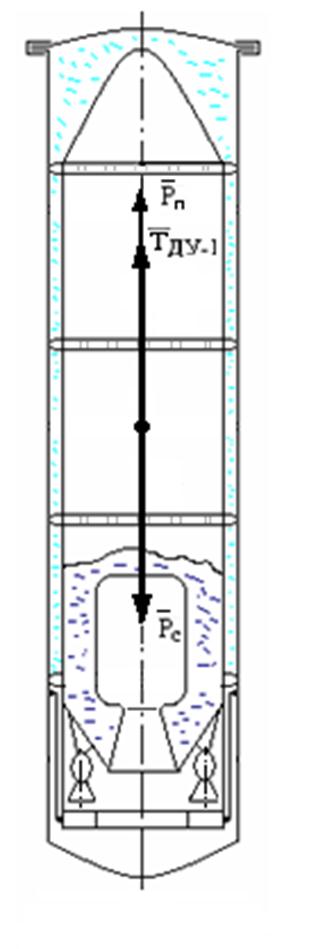
Рис. 1.1 Схема ШПУ с МБР.

Математическая модель процесса старта МБР с ЖРД.

Допущения:

1.  Изделие абсолютно твердое тело, движение изделия одномерное;

2.  Рабочие газы в подракетном объеме подчиняются уравнению состояния идеальных газов;

3.  Принимаем значение температуры рабочей смеси в подракетном объеме меньшим температуры насыщенных паров воды (температура принимается 330 – 360 К, жидкость несжимаемая);

4.  Влиянием ударно-волновых процессов на параметры движения изделия пренебрегаем;

5.  Трение поясов амортизации ракеты о стенки шахты учитывается коэффициентами по мере выхода каждого пояса амортизации из шахты.

Система уравнений.

1.  Уравнение изменения температуры газа в подракетном объеме.

,

2.  Уравнение изменения давления в подракетном объеме.

,

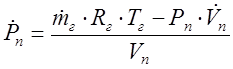3.  Уравнение изменения подракетного объема.

,

4.  Уравнение движения ракеты в шахте:

,

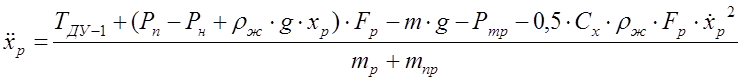где      - перемещение,

           - скорость,

           - ускорение.

 - присоединенная масса жидкости – фиктивная масса жидкости движущаяся с ускорением ракеты, энергия которой равна энергии реально движущихся частиц с разными скоростями в окрестностях головной части (ГЧ) ракеты. Зависит от формы ГЧ.

,

.

В начальный момент времени          ;

5.  Уравнение движения жидкости в кольцевом зазоре.

,

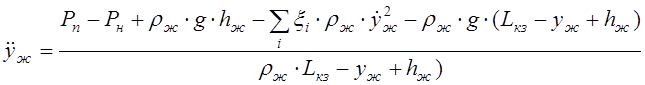где      - перемещение,

           - скорость,

           - ускорение.

Полученная система дифференциальных уравнений первого порядка решается методом Рунге-Кутта.

Начальные условия при :

1.	2.	3.
4.	5.	6.
7.	8.	9.

В результате решения системы дифференциальных уравнений определяются кинематические параметры движения ракеты и жидкости в кольцевом зазоре, а также газодинамические величины.

Исходные данные для выполнения расчета.

mp,кг	DШПУ,м	dр.м	Lр.м	Vвых±0,25,м/с	Ph,Па	V0,м3	Ккз
42000	2,2	2,0	13,8	19,2	4·105	0,35	0,75

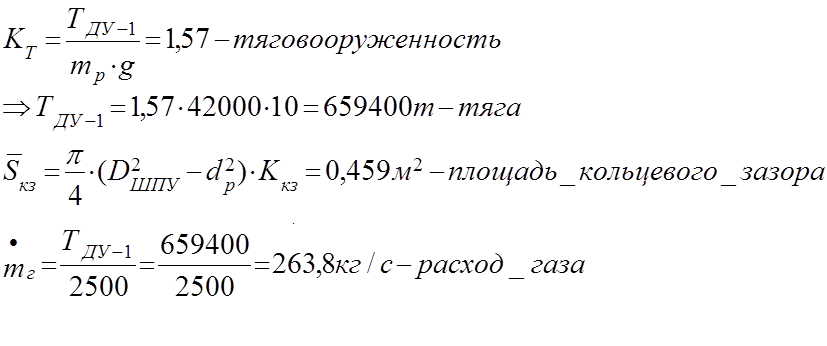
Результаты расчета.

В таблицу 1.1 сведены результаты расчета, полученные при выполнении программы «MBR_RX» с начальными данными представленными выше.

Таблица 1.1