6) Так как абсолютное отклонение случайной величины меньше утроенного стандартного отклонения (3 . 1,17 = 3,51), то выборка не содержит промахов и грубых выбросов.
7) Частотная классификация эмпирической выборки в пакете Microsoft Excel выполняется при помощи процедуры Гистограмма, имеющейся в надстройке Анализ данных (рисунок 4).
8) Заполним столбец В рабочего листа: в ячейки В1 : В5 введем варианты, имеющиеся в экспериментальных данных – 8, 9, 10, 11, 12. В пакете Microsoft Excel интервалы, в которые группируются данные, называются карманами.
9) Заполним открывшееся диалоговое окно, как показано на рисунке 6 и нажмем кнопку ОК.
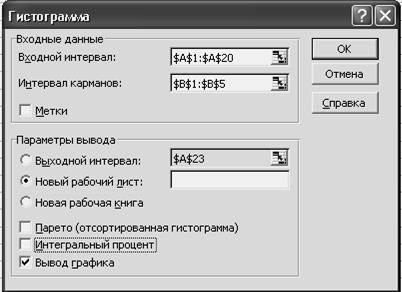
Рисунок 6 - Диалоговое окно: Гистограмма
10) Результаты расчета представлены на рисунке 7. На основании полученных результатов можно сделать вывод о том, что максимальная частота соответствует производству литейным цехом 10 бракованных отливок (относительная частота 6/20=0,3=30%), в данный интервал попало 6 наблюдений.
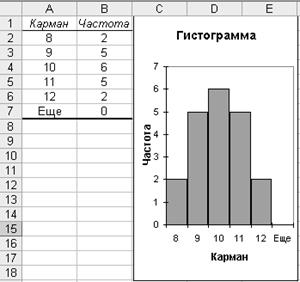
Рисунок 7 – Статистическое распределение выборки
11) Для определения доверительного интервала воспользуемся функцией ДОВЕРИТ. Она находится в диалоговом окне Мастер функций в категории статистические функции (рисунок 8). Результат расчета должен находиться в любой свободной ячейке рабочего листа Excel.
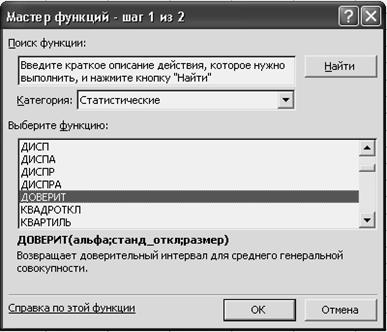
Рисунок 8 - Диалоговое окно Мастер функций
Доверительный интервал находится в зависимости от следующих параметров: уровня значимости – альфа
![]() (8)
(8)
(доверительную вероятность Р примем равной 95% или 0,95); стандартного отклонения случайной величины, значение которого мы уже определили (таблица 1) и размера выборки.
Заполним появившееся диалоговое окно Аргументы функции в соответствии с нашими данными и щелкнем ОК.
В нашем примере радиус доверительного интервала для среднего равен 0,5. Можно сделать вывод, что при количестве измерений n равном 20 среднее арифметическое случайной величины попадет в интервал [9,5; 10,5] с доверительной вероятностью 95 %.
12) По результатам проделанной работы необходимо составить отчет.
1) Фамилия, имя, отчество студента, группа.
2) Цель работы.
3) Описание исследуемых параметров случайной величины.
4) Значения точечных характеристик случайной величины, рассчитанные при помощи пакета прикладных программ Microsoft Excel в соответствии с индивидуальным заданием.
5) Статистическое распределение выборки в табличной и графической форме.
6) Результаты определения доверительного интервала для среднего арифметического.
7) Анализ полученных результатов и выводы о проделанной работе.
1) Что называется случайным событием?
2) Что называется вероятностью случайного события, как она определяется, в каких пределах изменяется?
3) Каким образом определяют уровень значимости случайной величины?
4) Что понимают под дискретной случайной величиной, под непрерывной случайной величиной? Приведите примеры из области литейного производства.
5) Что называют функцией распределения случайной величины? Как выглядит ее график?
6) Что называют плотностью распределения случайной величины? Как выглядит ее график?
7) Что представляет закон Гаусса? Почему он наиболее применим в экспериментальной практике?
8) Как звучит правило трех сигм? Для чего его используют?
9) Что такое генеральная совокупность и ее выборка?
10) Дайте определения следующим оценкам параметров выборочного распределения: размах варьирования, максимум, минимум, мода, медиана, среднее, стандартное отклонение, дисперсия, стандартная ошибка, эксцесс, асимметрия?
11) Как можно провести приближенную оценку соответствия эмпирического распределения нормальному?
12) Для чего используются интервальные оценки? Что такое доверительный интервал?
13) Что называется статистическим распределением выборки?
14) Каким образом влияют на форму нормальной кривой такие параметры как среднее, дисперсия?
15) Какие параметры служат для оценки «островершинности» и «скошенности» эмпирического распределения случайной величины?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.