Вероятностно-статистический анализ эксперимента: Методические указания к выполнению лабораторных работ по курсу «Основы научных исследований», страница 3

10)  Асимметрия (А) характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений (кривая плотности распределения сдвинута вправо относительно среднего значения). Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений (кривая плотности распределения сдвинута влево относительно среднего значения).

Коэффициенты асимметрии и эксцесса характеризуют вид нормального распределения и используются для приближенной оценки соответствия эмпирического распределения нормальному.

                                                       , ,                                        (7)

то можно с вероятностью 99,7 % сказать, что закон распределения случайной величины – нормальный.

Рассмотренные выше точечные оценки являются случайными величинами и их отклонения от соответствующих генеральных параметров также случайны. Кроме того, они не дают для выборок малого объема информации о точности конкретной оценки. Этот недостаток устраняется посредством использования доверительных или интервальных оценок, позволяющих по выборке определить интервал, в котором с заданной вероятностью – Р находится неизвестное истинное значение параметра распределения генеральной совокупности.

Таким образом, доверительный интервал среднего арифметического – интервал значений Х от х-z₁до х+z₂(z– радиус интервала, для нормального распределения z₁= z₂), попадание в который гарантируется с доверительной вероятностью Р.

Порядок выполнения работы

Статистическую оценку параметров распределения случайной величины в пакете Microsoft Excel выполняется при помощи специальной надстройки Анализ данных в раскрывающемся меню «Сервис» (рисунок 4).

Рисунок 4 - Диалоговое окно: Анализ данных

Рассмотрим определение параметров распределения на примере.

Пример. В течении 20 суток регистрировали количество бракованных отливок, изготовленных из чугуна в литейном цехе: 9, 11, 10, 11, 8, 11, 9, 12, 10, 8, 9, 10, 11, 10, 9, 11, 10, 9, 12, 10.

Необходимо:

а)  определить основные оценки выборочного распределения: среднее, стандартную ошибку, медиану, моду, стандартное отклонение, дисперсию выборки, эксцесс, асимметрию, размах, минимум, максимум;

б)  проверить является ли эмпирическое распределение нормальным;

в)  проверить выборку на наличие промахов, если таковые имеются, то исключить их из выборки;

г)  произвести частотную классификацию с группировкой данных в пять классов, и построить статистическое распределение случайной величины в виде гистограммы;

д)  определить доверительный интервал среднего арифметического значения измеряемой величины;

е)  произвести анализ полученных результатов.

1)  Для решения поставленной задачи заполним столбец А: введем в ячейки А1 : А20 рабочего листа экспериментальные данные.

2)  В меню Сервис выберем надстройку Анализ данных (рисунок 4). Для вычисления точечных оценок распределения случайной величины используется процедура Описательная статистика.

3)  Заполним открывшееся диалоговое окно, как показано на рисунке 5.

4)  После нажатия кнопки ОК на экране появится решение задачи, представленное в виде таблицы (таблица 1).

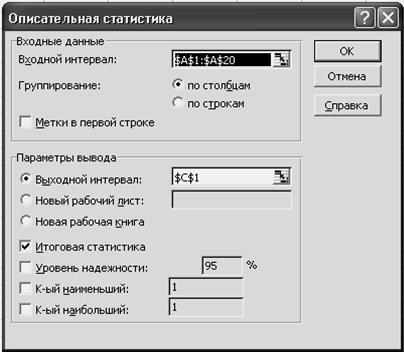
Рисунок 5 - Диалоговое окно: Описательная статистика

Таблица 1 - Результаты расчета

5)  Произведем анализ полученных результатов. Так как , то можно сделать следующий вывод: выборка имеет симметричный модальный закон распределения. Так как асимметрия и эксцесс по модулю меньше 3, то принимается нормальный закон распределения. Эмпирическая кривая симметрична относительно среднего, так как асимметрия равна 0 и имеет более плоскую вершину, так как эксцесс меньше 0 (вершина кривой плотности распределения случайной величины смещена вниз относительно кривой нормального распределения).