Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Сибирский государственный индустриальный
университет»
Кафедра литейного производства
Вероятностно-статистический анализ эксперимента
Методические указания к выполнению лабораторных работ по курсу
«Основы научных исследований»
Специальность «Литейное производство черных и цветных металлов» (110400)
Новокузнецк
2004
УДК 621.74
Ч 66
Рецензент:
кандидат технических наук, доцент, Куценко А. И.
Ч 66 Вероятностно-статистический анализ эксперимента: Метод. указ. / Сост.: О.Г. Приходько: ГОУ ВПО «СибГИУ». – Новокузнецк. 2004. – 18 с., ил.
Изложены рекомендации к выполнению лабораторной работы по обработке результатов эксперимента при проведении исследований в литейном производстве с применением пакета прикладных программ Microsoft Excel. Рассмотрены конкретные примеры выполнения расчетов на ЭВМ, что позволяет более ясно представить принципы использования методов математической статистики для решения технологических задач.
Предназначены для студентов специальности «Литейное производство черных и цветных металлов» (110400).
Широкое развитие средств вычислительной техники позволяет перейти на качественно новый уровень анализа экспериментальных данных в любых сферах деятельности человека. Под автоматизированной системой научных исследований (АСНИ) подразумевают систему для автоматизации процессов сбора данных, их обработки, хранения и выдачи результатов в удобном для анализа виде в ходе научных исследований.
Методы теории вероятности и математической статистики широко используются при проведении исследований в литейном производстве для изучения и совершенствования различных технологических процессов, контроля параметров этих процессов, разработки надежных методов оценки качества и приемки готовой продукции. Например, вероятностно-статистические методы позволяют объективно оценивать результаты испытаний физико-механических свойств; давать количественный анализ структуры деталей, изготовленных литьем; оценивать стабильность и надежность технологических процессов, агрегатов, используемых при производстве отливок; оценивать эксплуатационную стойкость и долговечность литых деталей и т. д.
Результаты экспериментов, т.е. фиксированные значения измеряемой величины, зависят от большого числа случайных причин, которые не могут быть учтены полностью. Поэтому при измерении одной и той же величины с одинаковой точностью фиксируемые результаты отличаются друг от друга. При этом наблюдается неконтролируемый разброс результатов, и предсказать результат последующего измерения невозможно. Следовательно, появление того или иного значения измеряемой величины является случайным событием, а результат любого единичного измерения – есть величина случайная. Поэтому для обработки измерений применимы методы математической статистики.
Цель данной работы – формирование у студента практических навыков автоматизированной обработки данных эксперимента и их анализа при проведении научных исследований в литейном производстве. Студент должен уметь определять характеристики распределения случайных величин, производить частотную классификацию экспериментальных данных и давать оценку полученным результатам. Кроме того, после проведения лабораторной работы студент должен уметь на практике использовать ЭВМ с имеющимся программным обеспечением.
Различают непрерывные и дискретные случайные величины.
Непрерывной случайной величиной Х называется такая величина, возможные значения которые могут сплошь заполнить интервал от x1до x2. Например: процентное содержание элемента в сплаве, твердость, прочность материала, производительность и др.
Дискретной случайной величиной Х называется такая величина, множество значения которой представляет собой последовательность чисел х1, х2,…,хn. Например: кол-во образцов, разрушившихся при испытаниях, количество отливок с дефектами и др.
Объективной мерой возможности появления того или иного значения случайной величины в результате эксперимента является частность или вероятность.
Вероятность появления случайного события А в конечном числе nопытов (наблюдений), проводимых в одних и тех же контролируемых условиях оценивается относительной частотой его появления Р(А) (0≤ Р(А)≤1).
Р(А)=![]() , где
l–
число появления случайного события А в n
независимых повторений.
, где
l–
число появления случайного события А в n
независимых повторений.
Для описания случайной величины необходимо указать все возможные значения, которые она может принимать – хi, а также указать вероятность появления каждого из значений – Р(хi), т. е. закон распределения. Он может быть задан таблично, аналитически или графически.
Для количественной характеристики распределения непрерывной случайной величины используется функция распределения (рисунок 1)
F(x)=P(X<x),
где Х – случайная величина, х – произвольное действительное число.
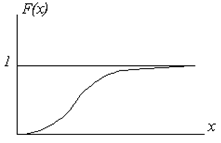
Рисунок 1 - График функции распределения непрерывной случайной величины
Более наглядно случайную величину можно представить с помощью функции плотности вероятности распределения случайной величины – р(х) (рисунок 2). Площадь, ограниченная осью абсцисс и кривой плотности распределения равна вероятности попадания случайной величины Х в интервал -∞<Х<+∞, т.е. равна единице.
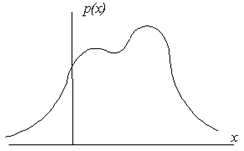
Рисунок 2 - Кривая плотности распределения непрерывной случайной величины
На практике наиболее часто встречается нормальный закон распределения, или закон Гаусса. Кривая плотности вероятности нормального закона распределения имеет куполообразную форму и называется нормальной кривой или кривой Гаусса (рисунок 3).
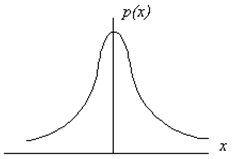
Рисунок 3 – Кривая Гаусса
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.