Вероятностно-статистический анализ эксперимента: Методические указания к выполнению лабораторных работ по курсу «Основы научных исследований», страница 2

Нормальный закон распределения наиболее часто используется в обработке экспериментальных данных, так как замена некоторого распределения нормальным не приводит к переоценке точности результатов. Это обусловлено тем, что нормальное распределение несет минимум информации по сравнению с другими распределениями при равенстве дисперсий.

Для нормального распределения справедливо «правило трех сигм»: абсолютное отклонение случайной величины от среднего значения не превышает утроенного стандартного отклонения. Это правило применяют для проверки нормальности распределения изучаемой величины и для выявления грубых ошибок (промахов) в экспериментальных данных.

Совокупность всех возможных (мыслимых) значений измеряемой величины называется генеральной совокупностью N.

Результаты эксперимента рассматриваются как часть некоторой генеральной совокупности, и называется выборкой или массивом экспериментальных данных. Выборочные характеристики являются лишь статистическими оценками генеральных характеристик.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот наблюдения. Наблюдаемые значения х_i называются вариантами. Числа наблюдений называются частотой – n_i, а их отношения к объему выборки n/n_i– относительными частотами.

Рассмотрим следующие выборочные характеристики распределения вероятности случайных величин:

1)  Максимум и минимум –  х_max, x_min – соответственно максимальное и минимальное значение случайной величины Х.

2)  Размах варьирования (интервал) – интервал изменения случайной величины.

                                                           R=х_max – x_min.                                        (1)

3)  Выборочное среднее (среднее арифметическое).

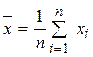                                                           ,                                        (2)

где n – размер выборки.

4)  Медиана – средневероятное значение случайной величины, для которого выполняется

                                                Р(х<х_мед)=Р(х>х_мед)=.                             (3)

Медиана — это число, которое является серединой вариационного ряда, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Вариационный ряд получается при расстановке всех случайных величин (вариант) в порядке возрастания.

5)  Мода – х_мод – значение случайной величины, которое имеет наибольшую вероятность.

Например: В литейном цехе производится плавка чугуна в вагранке. В процессе плавки производится отбор проб для химического анализа содержания углерода в чугуне. Получены следующие результаты (% С): 3,8; 3,9; 3,8; 3,8; 3,7; 3,8; 3,9; 3,8. Необходимо определить размах, моду и медиану.

х_max=3,9%, x_min = 3,7%. R=0,2%. х_мод = 3,8%.

Для определения медианы построим вариационный ряд: 3,7; 3,8; 3,8; 3,8; 3,8; 3,8; 3,9; 3,9. Так как объем выборки n= 8 – четное число, то медиана будет равна среднему арифметическому двух центральных чисел вариационного ряда х_мод = %.

6)  Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.

                                                σ=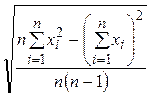.                                (4)

7)  Дисперсия выборки характеризует степень разброса случайной величины относительно среднего значения.

                                                  σ²=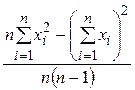.                                  (5)

8)  Стандартная ошибка определяется по формуле

                                                 ε=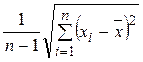,                                  (6)

9)  Эксцесс (Е) характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение (кривая плотности распределения сдвинута вверх относительно кривой нормального распределения). Отрицательный эксцесс обозначает относительно сглаженное распределение (кривая плотности распределения сдвинута вниз относительно кривой нормального распределения).