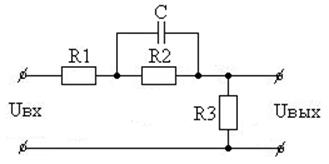
Вариант 22
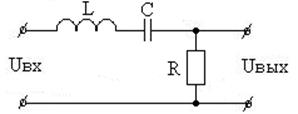
Вариант 23
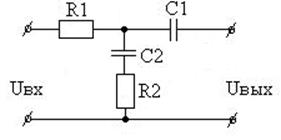
Вариант 24
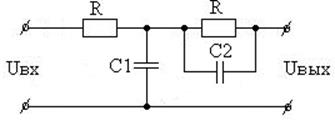
Вариант 25
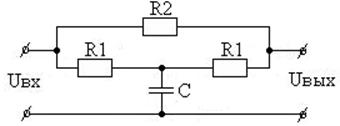
Вариант 26
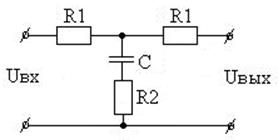
Вариант 27
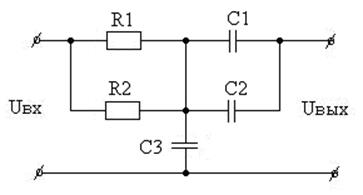
Вариант 28
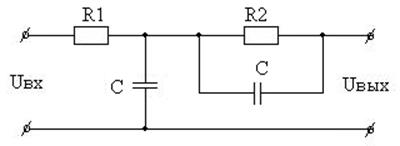
Вариант 29
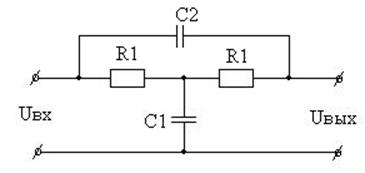
Вариант 30
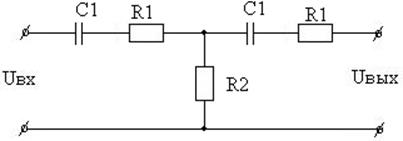
Вариант 31
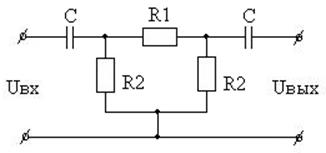
Вариант 32
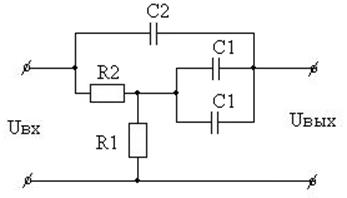
Вариант 33
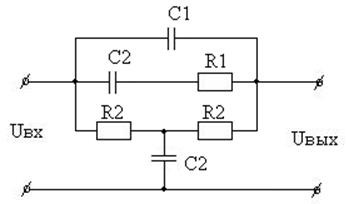
Вариант 34
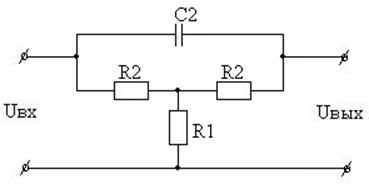
Вариант 35
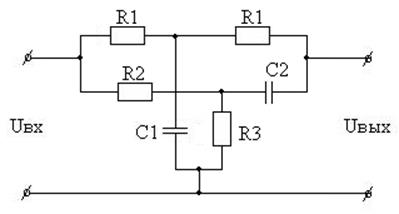
Вариант 36
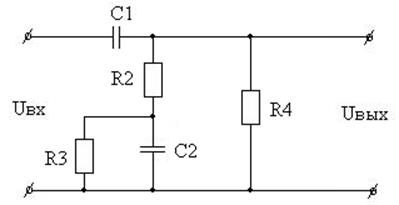
Вариант 37
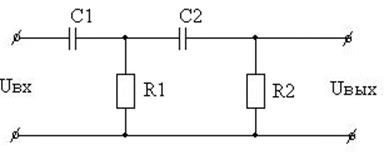
Вариант 38
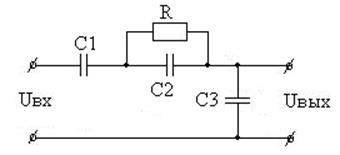
Вариант 39
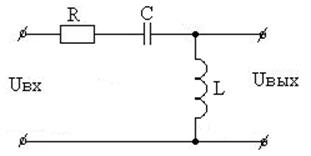
Вариант 40
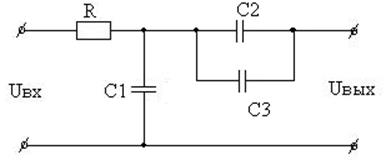
ПРИЛОЖЕНИЕ Б
Численные методы
Б.1 Метод Эйлера
Пусть дано дифференциальное уравнение
![]() (Б.1)
(Б.1)
с начальным условием у(х0) = у0.
Выбрав достаточно малый шаг h, построим систему равноотстоящих точек
![]() (i=0, 1, 2, …).
(Б.2)
(i=0, 1, 2, …).
(Б.2)
Искомую интегральную кривую у = у(х), проходящую,
через точку ![]() приближенно заменим (см. рис. Б.1)
ломаной
приближенно заменим (см. рис. Б.1)
ломаной ![]() ... с вершинами
... с вершинами ![]() (i=0, 1, 2, …), звенья которой
(i=0, 1, 2, …), звенья которой ![]() прямолинейны
между прямыми
прямолинейны
между прямыми ![]()
![]() и имеют
подъем
и имеют
подъем
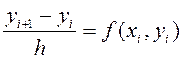 (Б.3)
(Б.3)
(так называемая ломаная Эйлера).
Таким образом, звенья ![]() ломаной Эйлера в каждой вершине
ломаной Эйлера в каждой вершине ![]() имеют направление
имеют направление![]() , совпадающее с направлением интегральной кривой уравнения (Б.1),
проходящей через точку
, совпадающее с направлением интегральной кривой уравнения (Б.1),
проходящей через точку ![]() .
.
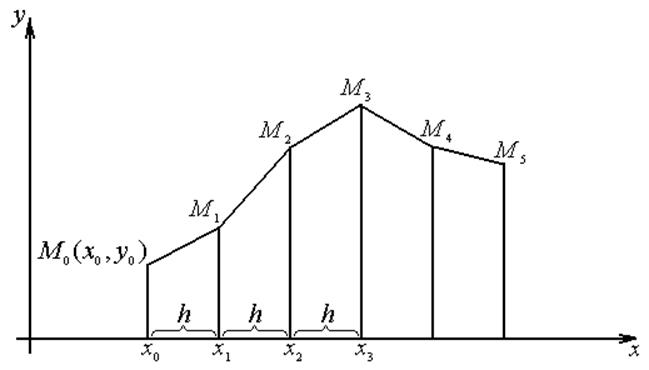
Рисунок Б.1 – Ломаная Эйлера
Из формулы (Б.3)
вытекает, что значения ![]() могут быть определены (метод
Эйлера) по формулам:
могут быть определены (метод
Эйлера) по формулам:
![]()
![]() (i=0, 1, 2, …).
(i=0, 1, 2, …).
Метод Эйлера является простейшим численным методом интегрирования дифференциального уравнения. Метод Эйлера легко распространяется на системы дифференциальных уравнений.
Б.2 Модифицированный метод Эйлера:
Модифицированный метод Эйлера применяется для приближенного решения дифференциальных уравнений второго порядка.
Решим приближенно дифференциальное уравнение второго порядка
![]() (Б.4)
(Б.4)
с
начальными условиями ![]() ;
; ![]() ,
,
Произведем в (Б.4) замену: ![]() .
.
Уравнение (Б.4) преобразуем в эквивалентную
нормальную систему для функций ![]() ,
, ![]() ;
;
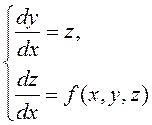 (Б.5)
(Б.5)
с
начальными условиями ![]() ;
; ![]()
Модифицированный метод Эйлера для системы (Б.5) таков же, как и метод Эйлера для одного уравнения. Вычисления идут двумя параллельными путями, причем результаты одного из них используются в другом по рекуррентным формулам:
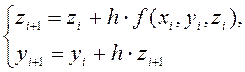 (i=0, 1, 2, …).
(i=0, 1, 2, …).
Б.3 Метод Рунге — Кутта
Пусть дано дифференциальное уравнение
![]() (Б.6)
(Б.6)
с начальным условием у(х0) = у0.
Выберем шаг hи для краткости введем обозначения
![]()
и
![]() (i=0, 1, 2, …).
(i=0, 1, 2, …).
Рассмотрим числа:
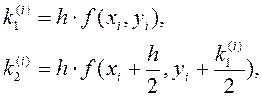
![]()
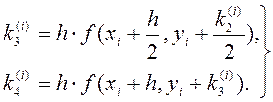 (Б.7)
(Б.7)
Тогда последовательные значения ![]() искомой функции
искомой функции ![]() определяются
по формуле:
определяются
по формуле:
![]()
где
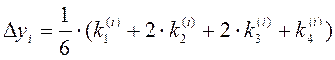 (i=0, 1, 2, …).
(i=0, 1, 2, …).
Приложение В
Образец оформления титульного листа
расчетно-пояснительной записки
Министерство образования Российской Федерации
Государственное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Кафедра автоматизированного электропривода и промышленной электроники
Отчет
по компьютерной практике
«Основы компьютерного моделирования. Исследование пассивного четырехполюсника»
Вариант №25
Номер зачетной книжки 01075
Выполнил студент гр. АПЭ-03
Иванов И.И.
Руководитель практики профессор Петров П.П.
Новокузнецк
2004
Составители:
Татьяна Вениаминовна Богдановская
Сергей Александрович Дружилов
Анатолий Константинович Мурышкин
Денис Сергеевич Лемешевский
Основы компьютерного моделирования.
Исследование пассивного четырехполюсника
Методические указания к прохождению
компьютерной практики для студентов специальностей
180400 «Электропривод и автоматика промышленных установок
и технологических комплексов»
и 200400 «Промышленная электроника» всех форм обучения
Утверждены на заседании кафедры автоматизированного
электропривода и промышленной электроники
«13» января 2004 г., протокол № 88,
и одобрены редакционной комиссией факультета автоматики,
информатики и электромеханики
![]()
Изд. лиц. № Подписано в печать
Формат бумаги 60х84 1/16. Бумага писчая. Печать офсетная.
Усл.печ.л. Уч.-изд.л. Тираж 60 экз. Заказ
![]()
Сибирский государственный индустриальный университет
654007, г. Новокузнецк, ул. Кирова, 42
Издательский центр СибГИУ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.