Основы компьютерного моделирования. Исследование пассивного четырехполюсника: Методические указания к прохождению компьютерной практики, страница 5

Пример: Найти , , ,  – параметры Т-образной схемы четырехполюсника.

Решение:

Заданная схема Уравнение в А - форме Составим уравнение для заданной схемы Решим уравнение (3) и (4) относительно  и , , ,   параметры

,                                                   (1) .                                                   (2) Применим метод контурных токов: ,                             (3) .                       (4) Из (4) ,                   (5) .(6) Сравнивая уравнения (5) и (6) с (1) и (2) получим ; . Сравнивая уравнения (1) и (4), имеем , .

6  ЭКВИВАЛЕНТНЫЕ СХЕМЫ ЗАМЕЩЕНИЯ ПРОХОДНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ

Было установлено, что любой реальный четырехполюсник характеризуется 3 коэффициентами. Если создать четырехполюсник, имеющий точно такие же коэффициенты, то реальный четырехполюсник можно заменить его эквивалентной схемой замещения и вместо реального четырехполюсника рассматривать его эквивалентную схему (см. рис. 1).

             

Г-образная схема                                        П-образная схема

Т-образная схема

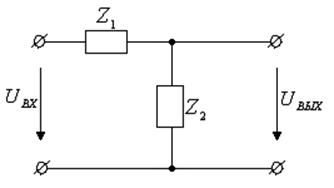
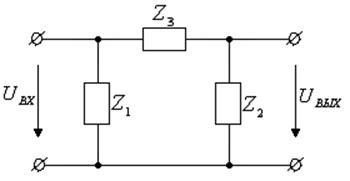
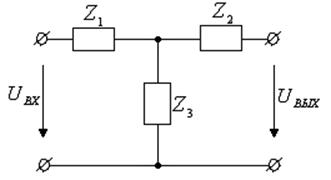
Рисунок 1 – Эквивалентные схемы замещения четырехполюсников

Таблица 3 – Определение параметров схем замещения через коэффициенты четырехполюсника

Эквивалентная схема	Параметр эквивалентной схемы в зависимости от коэффициентов четырехполюсника	Коэффициенты четырехполюсника в зависимости от параметров эквивалентной схемы

Таблица 4 – Эквивалентные преобразования соединения треугольником в звезду и соединения звездой в треугольник:

Существует несколько эквивалентных схем замещения (см. рисунок 1). Однако для всех эквивалентных схем выполняется следующее соотношение:

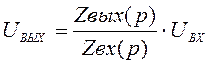.                                                (7)

Схема замещения будет физически реализована, если параметры элементов R, L и C будут положительны. Параметры схем замещения могут быть определены через коэффициенты реального четырехполюсника (см. таблицу 3).

Для того, чтобы четырехполюсник заменить его эквивалентной схемой без определения его коэффициентов, можно воспользоваться преобразованиями из таблицы 4.

7  ПРИМЕР РАСЧЕТА ПЕРЕХОДНОГО ПРОЦЕССА ПРОХОДНОГО ЧЕТЫРЕХПОЛЮСНИКА

Задание: получить математическое описание цепи, представленной на рисунке 1. По полученным разностным уравнениям написать моделирующую программу, которая выводит на экран график выходного напряжения в функции времени.

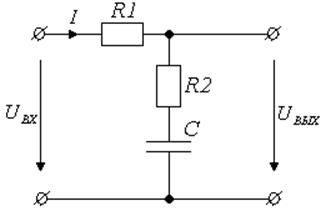
Рисунок 2 – Эквивалентная схема пассивного четырехполюсника

Решение:

При расчете переходного процесса будем использовать метод Эйлера (см. приложение А).

Определим выражение для выходного напряжения  в операторной форме. Для этого будем использовать операторную форму записи сопротивлений: индуктивного -, емкостного -  и активного - .

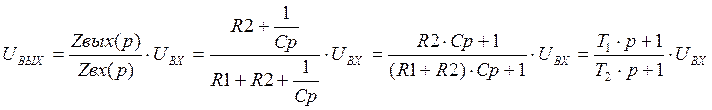, где      и – постоянные времени;

Выполнив подстановку, получим:

.                                                                 (8)

Заменяя  на y, на x,  получим выражение в общем виде:

,                                                                            (9)

где     p – оператор дифференцирования.

Заменяя p на , получим уравнение:

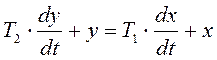.                                                                                    (10)

Используя метод Эйлера, перейдем к разностному уравнению:

,

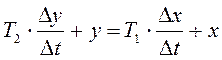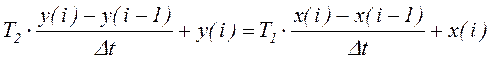,                                       (11)

где      и – значения сигналов в данный такт;

 и – значения сигналов в предыдущий такт.

,

,

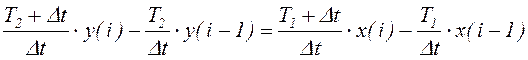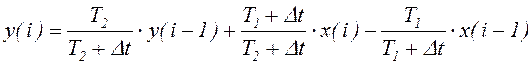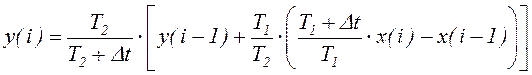.                                (12)

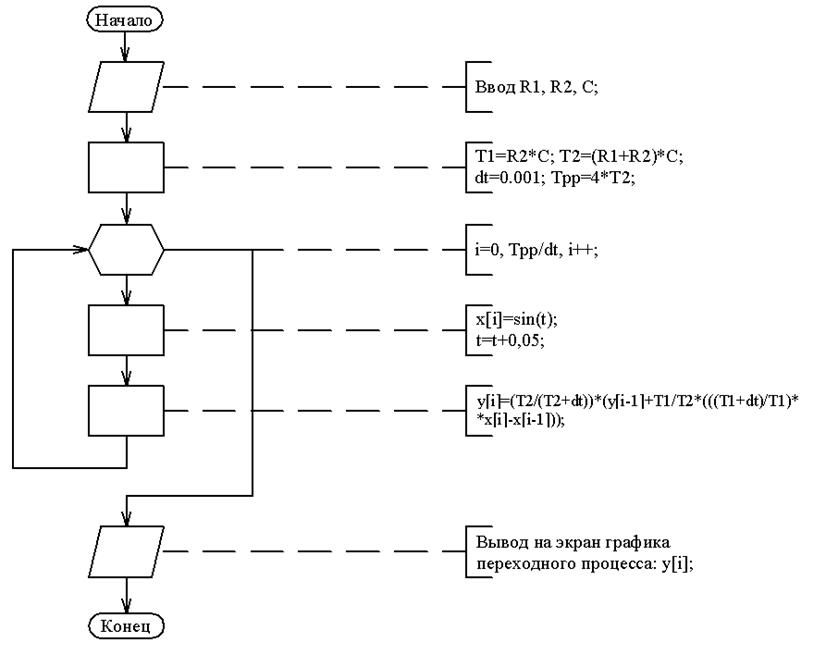
Рисунок 4 – Блок-схема алгоритма построения переходного процесса

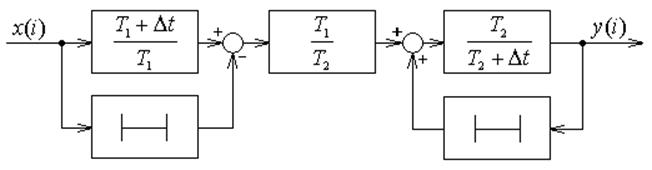
Алгоритмическая структура, соответствующая выражению (12) изображена на рисунке 3.

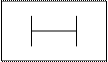где

– элемент, задержки сигнала на один такт.

Рисунок 3 – Алгоритмическая структура цифровой модели четырехполюсника

Блок – схема алгоритма построения переходного процесса представлена на рисунке 4.