Методические указания по выполнению лабораторного практикума по дисциплинам «Вычислительная математика», «Численные методы»

Новокузнецкий филиал-институт государственного образовательного учреждения высшего профессионального образования

«Кемеровский государственный университет»

Факультет информационных технологий

Кафедра математики и математического моделирования

Т.В. Бурнышева

ВЫЧИСЛИТЕЛЬНАЯ

МАТЕМАТИКА

часть 1

Методические указания по выполнению лабораторного практикума по дисциплинам

«Вычислительная математика», «Численные методы»

для студентов всех специальностей факультета информационных технологий

2011

Новокузнецк

СОДЕРЖАНИЕ

Введение. 5

РАЗДЕЛ 1. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОГО АНЛИЗА.. 6

1. Правила приближенных вычислений и оценка погрешностей при вычислении. 6

2. Обработка результатов наблюдений методом наименьших квадратов. 10

3. Выявление наилучшей аппроксимации для результатов наблюдений. 14

4. Интерполяционный многочлен Лагранжа. 17

5. Интерполяция сплайнами. 20

6. Интерполяционные многочлены Ньютона. 24

7. Численное дифференцирование. 27

8. Численное интегрирование. 32

РАЗДЕЛ 2. ЧИСЛЕННЫЕ МЕТОДЫ АЛЕБРЫ... 35

9. Решение алгебраических и трансцендентных уравнений комбинированным методом и половинного деления. 35

10. Решение алгебраических и трансцендентных уравнений методом простой итерации. 38

11. Прямые методы решения СЛАУ.. 41

12. Итерационные методы решения СЛАУ.. 44

Литература. 48

Введение

Проектирование, прочностной расчет современных машиностроительных конструкций и разнообразных технических систем связаны с теоретическими расчетами и исследованиями, определяющими выбор оптимальных параметров конструкций. Эти расчеты проводятся с использованием программных средств и реализованных в них численных методов или методов вычислительной математики. При решении прикладных задач, как правило, выполняются следующие этапы:

·  физическая постановка задачи,

·  поиск, выбор и модификация математической модели,

·  разработка, выбор или модификация математического метода,

·  составление алгоритма,

·  разработка программного обеспечения,

·  решение задачи и анализ результатов.

К классическим средствам изучения математических моделей относятся аналитические методы. Они позволяют получить точные решения в виде математических формул и дают наиболее полную информацию об объекте исследования, однако, касс задач для этих методов весьма ограничен. В настоящее время с развитием современных вычислительных машин широкое распространение получили численные методы расчета.

К численным методам принято относить методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям. Эти методы в отличие от аналитических позволяют найти частные решения, которые определяются не в континуальных, а дискретных областях изменения независимых переменных.

Численные методы, в связи с приближенностью вычислений, связаны с устойчивостью, зависящей от хорошей обусловленности задачи, сходимостью, точностью решения, экономичностью, с шагом дискретизации, равномерностью разбиения, количеством итераций и т.д.

В первой части разработанных методических указаний для выполнения лабораторного практикума по дисциплинам «Численные методы» и «Вычислительная математика» рассматриваются численные методы решения задач математического анализа и алгебры.

РАЗДЕЛ 1. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОГО АНЛИЗА

1. Правила приближенных вычислений и оценка погрешностей при вычислении

Цель работы: используя переменные а,b,c,d,e, данные с верными цифрами, вычислить значения функции S,U,V,W,P и их абсолютную и относительную погрешности. Результаты вычислений S,U,V,W,P округлить, оставив верные и одну сомнительную цифры.

ПРИМЕР. Дано: а=13,48;        b=121,51;    с=3,415.

Все цифры исходных данных верные. Требуется вычислить . Результаты округлить, оставив верные и одну сомнительную цифры.

Вычисляем абсолютные и относительные погрешности исходных данных. Абсолютную погрешность определяем исходя из того, что все цифры исходных данных верные. Относительную погрешность находим по формул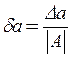е , где  - абсолютная погрешность приближенного числа а, А - точное число. Результаты вычислений представим в виде таблицы 1.1.

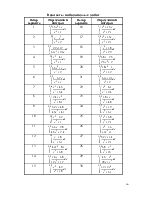
Таблица 1.1

Значение  вычисляется как сумма двух значений  и .

Тогда , а .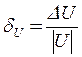

Вычислим  и :

1. 157,2067;                     0,00068;

0,1069.

2. 1,2229;

0,00041;

0,0005.

3. 158,4296;

0,10740,11;

0,00068.

Так как 0,11<0,5, то значение U содержит три верные значащие цифры (1, 5, 8), остальные цифры являются сомнительными. Округлим значение U, оставив только верные и одну сомнительную цифры. Данные представим в виде таблицы 1.2.

Таблица 1.2

Отчет по самостоятельной работе должен содержать:

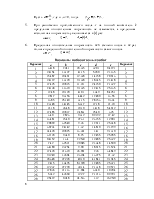
1.  Таблицу исходных данных, их абсолютных и относительных погрешностей (табл. 1.3);

2.  Заданные функции S, U, V, W, P и формулы по которым вычисляются их абсолютные и относительные погрешности;

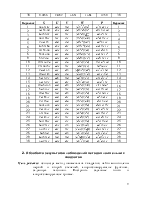
3.  Таблицу значений функций S S, U, V, W, P и их абсолютных и относительных погрешностей (табл. 1.4).

Таблица 1.3

Таблица 1.4

Теоретическая часть

Определение. Абсолютной погрешностью  приближенного числа а называют абсолютную величину  разности между точным числом