


Вариант 5
Цель работы: для функции, заданной таблично, найти приближенное значение функции в
точках ![]() ,
, ![]() и
значение производной в точке
и
значение производной в точке ![]() .
.
Функция Г
|
x |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
f(x) |
0,99602 |
1,07670 |
1,15402 |
1,22777 |
1,29776 |
1,36386 |
1,42592 |
1,48384 |
1,53751 |
1,58688 |
Точки интерполяции
|
N |
|
|
|
|
7 |
0,03 |
0,86 |
0,02 |
ПРИМЕР. Функция задана таблицей 6.1.
Требуется найти приближенное значение функции ![]() в
точках
в
точках ![]() =0,03;
=0,03; ![]() =0,86 и
значение производной функции в точке
=0,86 и
значение производной функции в точке ![]() =0,02.
=0,02.
Таблица 6.1
|
x |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
|
f(x) |
0,99602 |
1,07670 |
1,15402 |
1,22777 |
1,29776 |
1,36386 |
1,42592 |
1,48384 |
Составим таблицу конечных разностей 6.2 для исходной функции. Таблицу обрываем на четвертых разностях, так как конечные разности четвертого порядка практически постоянны.
Точка ![]() =0,03 находится в начале таблицы
6.1, поэтому воспользуемся первым интерполяционным многочленом Ньютона
=0,03 находится в начале таблицы
6.1, поэтому воспользуемся первым интерполяционным многочленом Ньютона
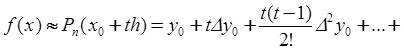
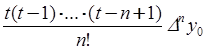
при
![]() ;
; ![]() ;
; ![]() ;
; 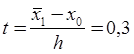 .
.
Имеем
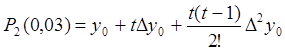
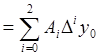 .
.
Таблица 6.2
|
x |
y |
D y |
D2 y |
|
0 |
0,99602 |
||
|
0,0807 |
|||
|
0,1 |
1,0767 |
-0,0034 |
|
|
0,07732 |
|||
|
0,2 |
1,15402 |
-0,00357 |
|
|
0,07375 |
|||
|
0,3 |
1,22777 |
-0,00376 |
|
|
0,06999 |
|||
|
0,4 |
1,29776 |
-0,00389 |
|
|
0,0661 |
|||
|
0,5 |
1,36386 |
-0,00404 |
|
|
0,06206 |
|||
|
0,6 |
1,42592 |
-0,00414 |
|
|
0,0579 |
|||
|
0,7 |
1,48384 |
||
Вычисления представим в виде таблицы 6.3.
Таблица 6.3
|
i |
0 |
1 |
2 |
|
Ai |
1 |
0,3 |
-0,105 |
|
Di y0 |
0,99602 |
0,0807 |
-0,0034 |
Ответ: ![]() .
.
Вычисления производим с шестью знаками после запятой. В ответе последний знак отбрасываем.
Точка ![]() =0,86 находится в конце таблицы 6.1,
поэтому воспользуемся вторым интерполяционным многочленом Ньютона
=0,86 находится в конце таблицы 6.1,
поэтому воспользуемся вторым интерполяционным многочленом Ньютона
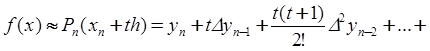
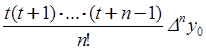
при
![]() ;
; ![]() ;
; ![]() ;
; 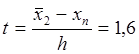 .
.
Имеем
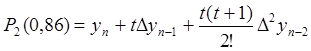
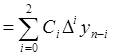 .
.
Вычисления представим в виде таблицы 6.4.
Таблица 6.4
|
i |
0 |
1 |
2 |
|
Сi |
1 |
1,6 |
2,08 |
|
Diyn-1 |
1,48384 |
0,0579 |
-0,00414 |
Ответ: ![]() .
.
Вычисления производим с шестью знаками после запятой. В ответе последний знак отбрасываем.
В таблице 6.2 конечных разностей жирным шрифтом выделены конечные
разности, используемые при вычислении ![]() и
и ![]() .
.
Вычислим значение
производной функции ![]() в точке
в точке ![]() =0,02.
Значение аргумента
=0,02.
Значение аргумента ![]() =0,02 находится в начале таблицы
6.1. Построим интерполяционный многочлен второй степени по первой
интерполяционной формуле Ньютона:
=0,02 находится в начале таблицы
6.1. Построим интерполяционный многочлен второй степени по первой
интерполяционной формуле Ньютона:
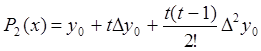 .
.
Производную функции вычисляем приближенно из соотношения:
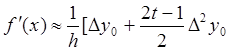 ].
].
В
данном случае ![]() ;
; ![]() ;
; 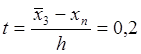 .
.
Подставляя h, t,
значения конечных разностей из таблицы 6.2 в выше приведенную формулу, получаем
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.