Анализ технологического процесса, формирование требований предъявляемых техпроцессом к АЭП. Расчет статических нагрузок. Построение приближенных нагрузочной и скоростной диаграмм механизма, страница 3

Расчет динамических нагрузок электропривода. Построение приближенных нагрузочной и скоростной диаграммы электропривода за цикл работы. Предварительная проверка выбранного двигателя по нагреву пусковой и перегрузочной способностям.

Передаточное число.

Отношение угловых скоростей  (частот вращения), радиусов шестерен, находящихся в зацеплении, шкивов, соединенных ремнями, звездочек, соединенных цепью, называют передаточным числом. При жестком зацеплении передаточное число определяется следующим образом:

;

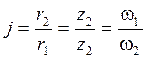где r1, r2 – соответственно радиусы ведущего и ведомого колес;

z1, z2 – число зубьев ведущего и ведомого колес;

ω1, ω2 – угловые скорости ведущего и ведомого валов.

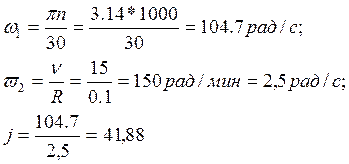
Выбираем редуктор с передаточным числом равным 44. По справочнику выбираем редуктор.

Определим статические моменты механизма, разделив мощность на угловую скорость:

              

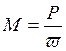
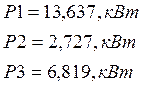
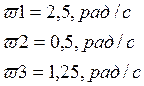
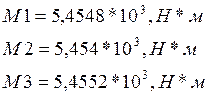
Статический момент на валу рабочей машины, приведенный к валу электродвигателя, без учета потерь в передаче определяется выражением:

;

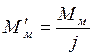где Мм – момент сопротивления на валу рабочей машины;

j – передаточное число редуктора.

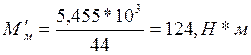
В общем случае для двигательного режима, статический момент на валу двигателя с учетом потерь в передаче равен:

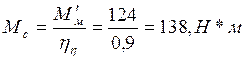
Момент инерции электропривода.

Суммарный момент инерции электропривода определяется следующим образом:

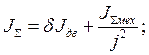
где δ=1,15÷1,3 – коэффициент, учитывающий момент инерции вращающихся масс передаточного механизма;

Jдв – момент инерции ротора двигателя =0,534 кг*м²;

 – суммарный момент инерции механизма;

j – передаточное число редуктора.

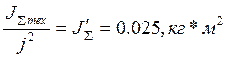
Нагрузочная диаграмма электропривода представляет собой зависимость электромагнитного момента М, тока I или мощности Р от времени. В тех случаях, когда момент и ток связаны линейной (или примерно линейной) зависимостью, обычно нагрузочную диаграмму строят для момента, который определяют из основного уравнения движения электропривода:

;

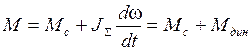где Мс – статический момент на валу двигателя;

Мдин – динамический момент электропривода;

JΣ – суммарный момент инерции электропривода кг·м².

Динамический момент электропривода Мдин определяют предварительно приближенно, принимая линейным закон изменения скорости, т.е.

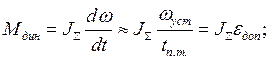
где ωуст – установившаяся скорость двигателя на данном участке скоростной диаграммы, рад/с ;

tп.т. – время пуска (торможения), с;

εдоп – допустимое угловое ускорение (замедление), рад/с.

.

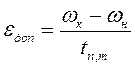Определим угловое ускорение. Для этого предположим, что время разгона нашего двигателя до номинальной скорости будет равно 2 секунды, тогда:

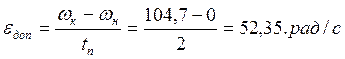
Теперь, считая угловое ускорение постоянным, найдем времена разгона и торможения:

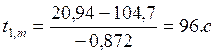
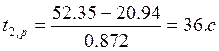
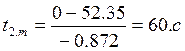
Определим динамический момент:

По основному уравнению электропривода строим приближенную нагрузочную и скоростную диаграммы.

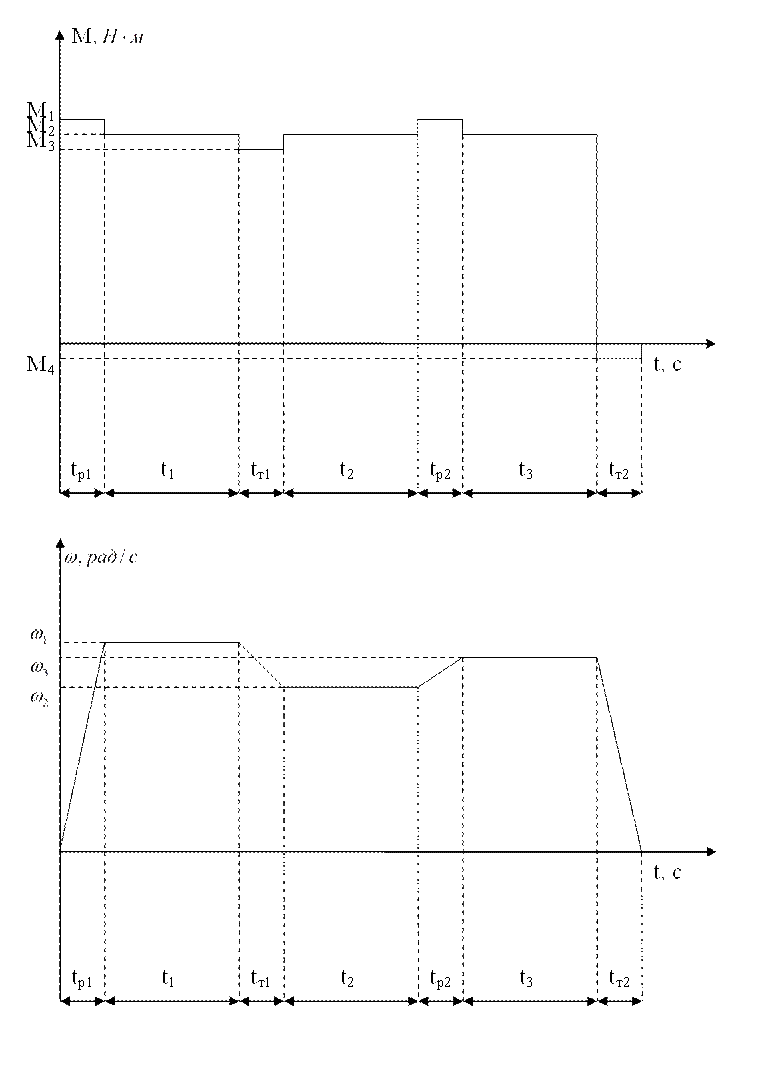
Рис.3.1. Приближенные нагрузочная и скоростная диаграммы электропривода.

М₁=171,45; М₂=138; М₃=104,55; М₄=-33,45.

t_p1=0,2мин; t₁=90мин; t_t1=1,6мин; t₂=120 мин; t_p2=0,6 мин; t₃=90мин;

t_t2=1 мин

Перейдем к проверке двигателя по нагреву. В нашей системе электропривода выбранный электродвигатель будет работать при примерно постоянном магнитном потоке (т.к. регулирование будет осуществляться при Ф=const). Тогда для расчета воспользуемся методом эквивалентных моментов, который заключается в том, что при данном регулировании среднеквадратичный момент электродвигателя отражает его температуру нагрева.

;

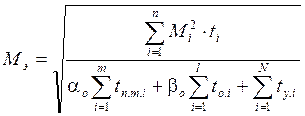где αо – коэффициент ухудшения условий охлаждения при пуске, торможении двигателя с самовентиляцией ( αо≈0,5 для асинхронных двигателей);

βо – коэффициент, учитывающий ухудшение охлаждения самовинтелируемого двигателя при отключении;

tо.i – продолжительность i-ой паузы;

tn.m.i – продолжительность пуска (торможения) на i-ом интервале;