Электромеханические переходные процессы
Электромеханические переходные процессы электропривода с линейной механической характеристикой при ω0 =const. В системах электропривода с линейной механической характеристикой скорость идеального холостого хода ω0 является обобщенным управляющим воздействием. Его значение определяется в электроприводах постоянного тока приложенным к якорной цепи двигателя напряжением uЯ, а в электроприводах переменного тока – частотой тока статора fs. Один из вариантов переходных процессов – это процессы, протекающие при постоянном значении ω0. При этом они могут быть вызваны:
– включением двигателя на напряжение питания, когда ω0 скачком изменяется от нуля до ω0.ном, что характеризует его пуск,
– изменением знака ω0.ном также скачком, что характеризует режим торможения противовключением с последующим разгоном в противоположном направлении, т. е. реверс,
– отключением двигателя от напряжения питания и включения его по схеме динамического торможения, когда ω0 скачком уменьшается от ω0.ном до нуля, что характеризует динамическое торможение,
– изменением нагрузки на валу двигателя (скачок нагрузки).
При расчете переходных процессов, возникающих в результате скачкообразного изменения управляющего или возмущающего воздействия целесообразно учитывать электромагнитную инерционность двигателя Тэ ≠ 0. Тогда электромеханические переходные процессы в системах с линейной механической характеристикой при ω0 = const и с12 = ∞ с учетом уравнения движения описываются следующими уравнениями
.
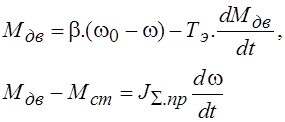Решив второе уравнение относительно Мдв и подставив его в первое уравнение, получим дифференциальное уравнение системы, решенное относительно скорости
.
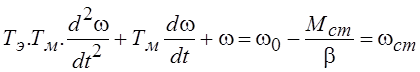Аналогично можно получить дифференциальное уравнение системы, решенное относительно момента:
.
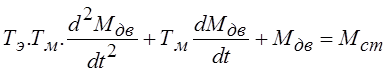Анализ корней приведенных характеристических уравнений дает два случая, когда Тм / Тэ < 4 и когда Тм / Тэ > 4.
В первом случае корни имеют следующее выражение
.
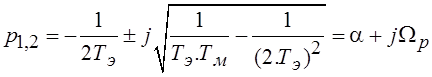Общее решение уравнения относительно скорости традиционными методами математики дает следующее выражение
.
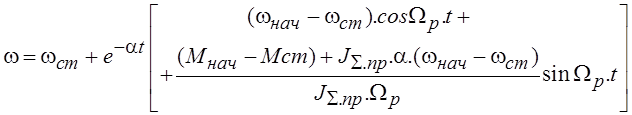Общее решение уравнения относительно момента дает следующее выражение
.
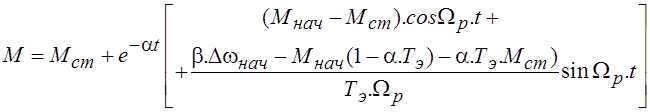Во втором случае корни имеют следующее выражение р1 = – α1, р2 = – α2.
Общее решение уравнения относительно скорости традиционными методами математики дает следующее выражение
.
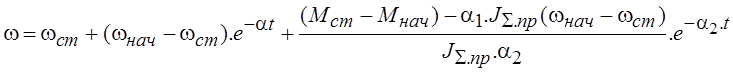Общее решение уравнения относительно момента дает следующее выражение
.
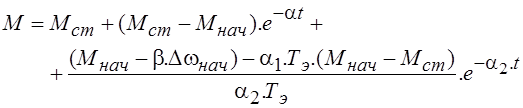Полученные решения позволяют рассчитать все перечисленные выше переходные процессы при ω0 = const при любых начальных условиях и сочетании параметров.
Электромеханические переходные процессы электропривода с линейной механической характеристикой при ω0 =f(t). В системах регулируемого электропривода, где переходные процессы формируются изменением напряжения, подводимого к обмотке якоря двигателя, или частоты тока, протекающего по обмоткам статора двигателя переменного тока, они протекают при ω0 =f(t), при чем законы изменения скорости идеального холостого хода могут быть от линейного до любой другой зависимости. Наиболее часто встречается линейный закон ω0 (t)=ω0.нач + ε0 .t. Тогда дифференциальное уравнение системы, решенное относительно скорости будет иметь вид
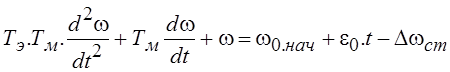, где Δωст =Мст
.β. В силу возможности плавного изменения управляющего воздействия влияние
электромагнитной инерции на протекающие переходные процессы незначительно,
поэтому можно принять Тэ≈0 и дифференциальное уравнение упрощается:
,
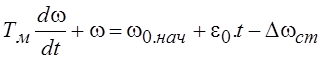Приведенное уравнение имеет правую часть, линейно зависящую от времени. Решение такого уравнения имеет следующее выражение
.
Дифференциальное уравнение системы, решенное при Тэ≈0 относительно момента двигателя, имеет вид
.
Примерный вид переходных процессов зависимостей ω(t) и М(t) для случая, когда предшествующий режим был неустановившимся и Мст ≠0, приведен на рис. .
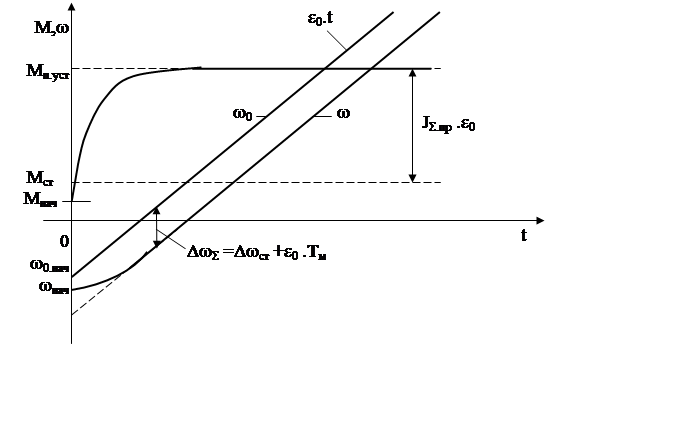
Рис.
Линейное изменение управляющего воздействия не приводит на начальном этапе движения электропривода к линейному изменению его скорости в силу наличия свободной составляющей этого процесса. Длительность начального участка переходного процесса зависит от электромеханической постоянной времени и заканчивается (затухает свободная составляющая) за время равное (3…4) Тм. В дальнейшем идет линейное нарастание скорости с отставанием от линейного задания управляющего воздействия на значение равное ΔωΣ =Δωст + ε0 . Тм. Это отставание и определяет ошибку воспроизведения скорости. Ошибка складывается из ошибки, равной статическому падению скорости Δωст = Мст /β, и ошибки, равной динамическому падению скорости Δωдин = JΣ.пр . ε0/β. Они определяются по статической механической характеристике полным моментом двигателя
Мст + JΣ.пр . ε0. Например, для двигателя постоянного тока величина ΔωΣ пропорциональна падению напряжения на якорной цепи от полного тока
ΔωΣ = (Мст + JΣ.пр . ε0) /β= (Iст + Iдин).RЯ.Σ /с. Уменьшение воспроизведения достигается увеличением модуля жесткости статической механической характеристики.
Существенное влияние на переходный процесс при плавном изменении управляющего воздействия оказывает влияние характер момента нагрузки. Рассмотрим переходный процесс пуска электропривода с реактивным моментом статического сопротивления. Он распадается на три этапа. На первом этапе возрастания ω0 =ε0.t происходит линейное возрастание момента двигателя по закону Мдв = ε0.t .β до тех пор, пока Мдв ≤ Мст, при этом скорость равна нулю, поскольку электропривод заторможен реактивным моментом нагрузки. Этот этап определяет время запаздывания начала движения tзап = Мст / ε0 / β и заканчивается, когда Мдв = Мст. Второй этап это движение электропривода при условиях ω0.нач =Δωст, ωнач=0, Мдв = Мст описывается следующими выражениями
.
Каждому текущему значению ω0 соответствует определенная механическая характеристика двигателя, рис. .
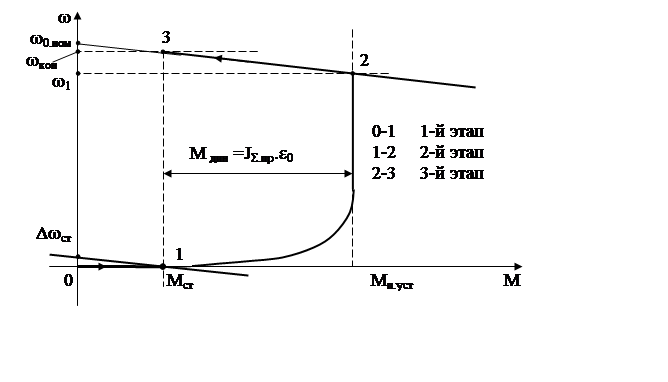
Рис.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
