Электромеханические переходные процессы электропривода с линейной механической характеристикой, страница 3

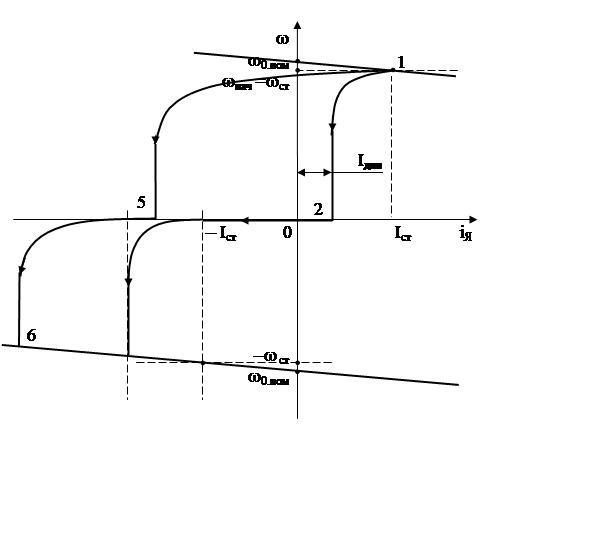
В случае механизма с реактивным моментом статического сопротивления процесс реверса протекает несколько сложнее. Рассмотрим этот процесс на конкретном электроприводе – на электроприводе с двигателем постоянного тока с двигателем независимого возбуждения. Соответствующие механические характеристики приведены на рис.    .

Рис.

Здесь процесс замедления аналогичен процессу торможения в случае работы электропривода с активной нагрузкой. Начальная разность между напряжением на якоре u_Я и ЭДС двигателя Е_дв =сω_ст, равная падению напряжения на сопротивлении якоря от статического тока I_ст.R_Я.Σ, уменьшается до значения, равного падению напряжения от установившегося тока при реверсе I_р.уст= I_дин= М_дин/с. Ток якоря при этом уменьшается от начального значения I_ст до I_р.уст, а затем он остается постоянным до скорости, равной нулю. Зависимости  ЭДС е_Я(t) и тока двигателя i_Я(t) приведены на рис.    .

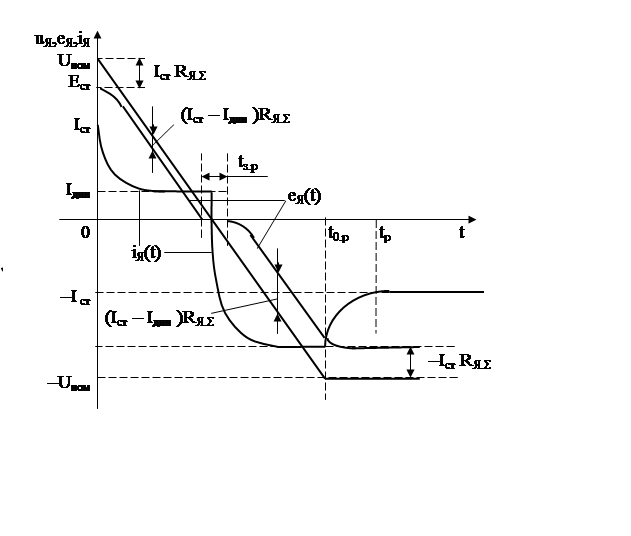
Рис.

В момент прохождения скорости через нуль реактивный момент нагрузки изменяется скачком от М_ст до – М_ст. Поэтому для разгона двигателя в противоположном направлении ток должен поменять знак за счет изменения знака управляющего воздействия, а затем увеличиваться по модулю до значения, превышающему модуль статического тока. Так появляется пауза в движении t_з.р, в течение которой ток якоря нарастает по закону

i_Я =I_дин – с.ε₀.t/R_Я.Σ , а скорость ω=0. Из приведенного выражения определяется время запаздывания в момент i_Я = – I_ст:  t_з.р= (I_дин + I_ст).R_Я.Σ / с.ε₀.t. В дальнейшем разгон в противоположном направлении описывается аналогичными уравнениями предыдущего случая. Динамическая электромеханическая характеристика процесса реверсирования электропривода с реактивным моментом нагрузки приведена на рис.   , кривая 1-2-3-4.

Если увеличить темп изменения управляющего воздействия du_Я /dt, то вследствие роста динамического тока при торможении ток (I_ст–I_дин) уменьшается до нуля, а потом изменяет знак, при этом время запаздывания уменьшается. При  I_ст = – I_дин это время становится равным нулю, при этом из уравнения движения  (– М_дв  – М_ст = J_Σ.пр.ε₀ ) можно определить значение ε_0.1:

ε_0.1 = – 2М_ст / J_Σ.пр = – 2М_ст / β.Т_м.

Если |ε_0.1| > |ε_0.1|, то процесс изменения скорости при реверсе является непрерывным и влияние реактивного момента нагрузки сказывается лишь на изменении скачкам ускорения при переходе скорости через нуль. Динамическая электромеханическая характеристика процесса реверсирования электропривода для этого случая приведена на рис.   , кривая 1-5-6-4.

Рассмотренные переходные процессы позволяют сделать общий вывод о том, что закон изменения напряжения u_Я для электропривода постоянного тока или частоты f_s  для электропривода переменного тока  определяет характер изменения скорости  в переходном процессе с тем большей точностью, чем меньше электромеханическая постоянная времени Т_м = J_Σ.пр / β. Этот вывод действителен и для любого другого закона изменения управляющего воздействия.