Модернизация системы автоматического управления процесса полимеризации (Раздел 3 дипломного проекта)

окружность вырождается в точку с координатами [-1;j0]. Затем на рассматриваемой комплексной плоскости строится АФЧХ. Наименьшая окружность, которой коснется АФЧХ, определит значение М рассматриваемой системы.

Если при проектировании системы ставится условия, чтобы ее показатель колебательности был не больше некоторого заданного, то для выполнения этого необходимо, чтобы амплитудно-фазовая характеристика не заходила внутрь окружности, соответствующей этому значению М. Амплитудно-фазовая характеристика может только коснуться этой окружности. В этом случае показатель колебательности будет как раз равен заданному значению рис. 3.3:

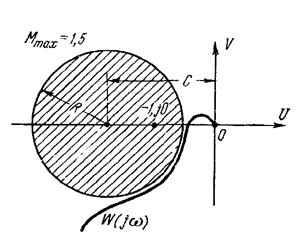
Рис.3.3. Амплитудно-фазовая характеристика при показатели колебательности равном желаемому.

Таким образом, окружность является запретной зоной для амплитудно-фазовой характеристики разомкнутой системы. Эта зона охватывает точку (1, j0) и обеспечивает получение заданного запаса устойчивости.

Для синтеза регулятора зададимся М=1.18. При передаточной функции разомкнутой системы необходимо подобрать такие коэффициенты регулятора, чтобы  касалась окружности с желаемым значением М. Можно это делать подбором коэффициентов, однако, желательно иметь какие – либо правила, которые уменьшили бы число настроек. Построим окружность с желаемым М, и проведём к ней касательную.

Принимаем, что пропорциональная составляющая передаточной функции регулятора К=1. Задавшись постоянной интегрирования (например, Ти=1), строим АФЧХ разомкнутой системы. Проводим луч из начала координат с углом наклона:

                                                                                                        (3.6)

Далее строим окружность с центром, лежащим на оси абсцисс так, чтобы она коснулась прямой и нашей АФЧХ. Восстановив перпендикуляр в точке касания прямой и окружности к оси абсцисс, получим значение А. Далее задаваясь другими значениями постоянной интегрирования строим новые АФЧХ и повторяем операцию с построением окружности. Получив набор постоянных интегрирования и соответствующим им коэффициентов усиления, строим кривую . Проводим из начала координат касательную к кривой, и в точке касания мы получим оптимальные значения k и Т_и, при подстановке которых в передаточную функцию, АФЧХ разомкнутой системы коснется окружности с заданным показателем колебательности.

Принимаем коэффициент пропорциональности регулятора К=1 и, задавшись значениями постоянной времени регулятора, строим АФЧХ разомкнутой системы, луч из начала координат с углом наклона:

                                                                                (3.7)

По изложенной методике рассчитан ПИ регулятор, расчёт выполнен в пакете Matlab, расчёты приведены ниже, а также показаны на плакате расчёта регулятора и моделирования системы.

Расчет параметров ПИ-регулятора

% clear - очистка ячеек памяти от всех переменных;

% clc - очистка  содержимого командного окна;

% clf - очистка графического окна;

clc, clf, clear;

% задаем передаточную функцию объекта;

% tf - transfer function - передаточная функция;

% tf([числитель], [знаменатель], ...)

ww=tf([2,465],[55496,9 1]);

% вывод графика АФЧХ (диаграмма Найквиста);

figure(1);

nyquist(ww);

% задаем величину желаемого показателя качесва Мжел.;

M=1.18;

w=0:0.0005:2;

% задаем величину коэффициента пропорцианальности

kp=0.7;

% подбираем постоянную времени интегрирования (время изодрома) т.о., чтобы окружность коснулась АФЧХ

Tiz=700;

% заменяем p на jw для перехода в комплексную область

p=j*w;

www=kp.*(1+1./(Tiz.*p))*2.465./( 55496.9*p+1);

% создаем функции для изображения АФЧХ в комплексной области;

Re=real(www);

Im=imag(www);

% объявляем радиус окружности

R=M/(1-M^2);

% C - расстояние от мнимой оси до центра окружности;

C=M^2/(1-M^2);

x=-2:0.005:0;

% Геометрия x^2 + y^2 = R^2 - формула, описывающая окружность

% y1 - верхняя часть окружности; y2 - нижняя часть окружности;

y1=sqrt(R^2-(x-C).^2);

y2=-sqrt(R^2-(x-C).^2);

% k - тангенс угла наклона касательной к окружности

k=tan(asin(1/M));

% задаем уравнение прямой;

y3=k*x;

figure(2);

plot(Re, Im, x, y1, 'r', x, y2, 'r', x, y3);

% grid - вывод "сетки" на графике;

grid on;

% задаем вектор значений kp;

kp=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];

% % задаем вектор значений Tiz;

Tiz=[0 152 222 296 357 418 512 700];

% строим график зависимости kp от Tiz к которому затем проведем;  касательную и найдем оптимальный вариант значений kp и Tiz;

figure(3);

plot(Tiz, kp);

grid on.

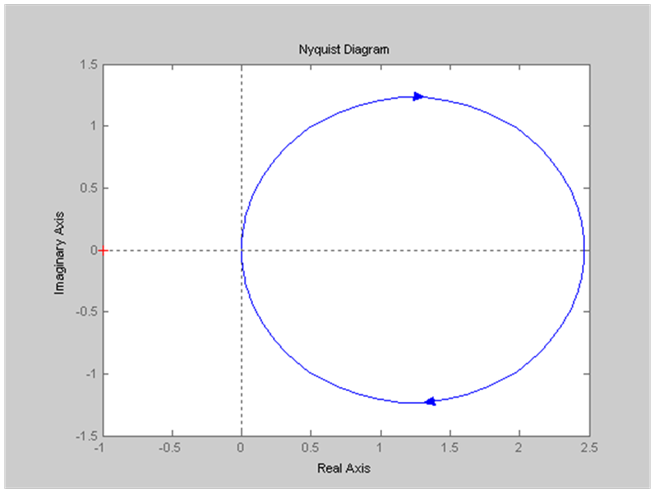
Рис. 3.4. АФЧХ (диаграмма Найквиста)

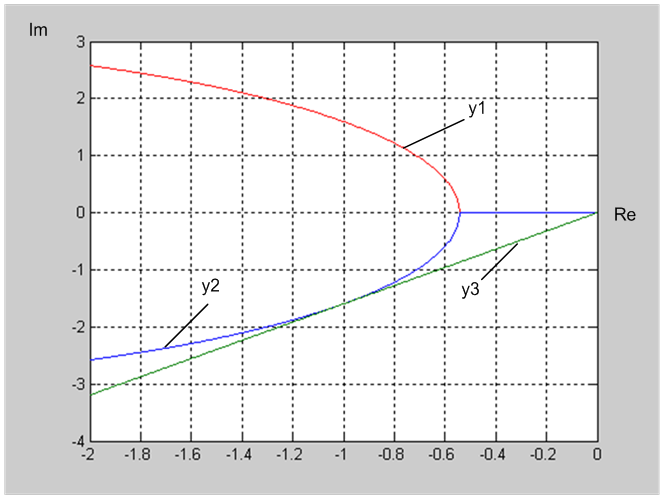
Рис. 3.5. Амплитудно-фазовая характеристика регулируемого объекта

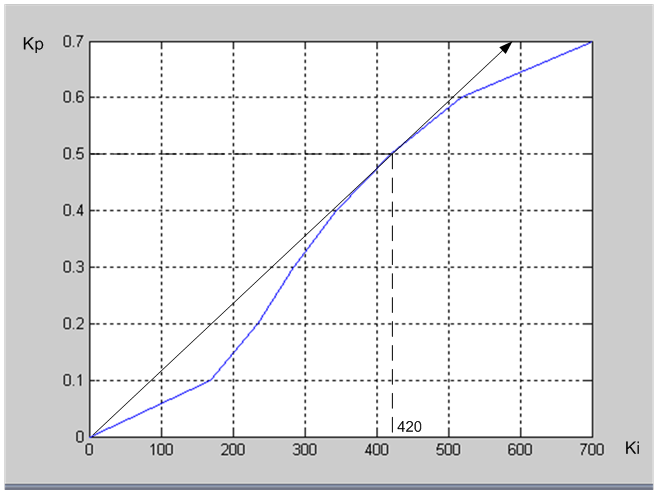
Рис. 3.6. График зависимости Kp от Ki

Значение Ti находится из выражения:  ;                       (3.8)

Коэффициент передачи клапана:  ;                             (3.9)

В качестве датчика был выбран бесконтактный радарный датчик уровня, его коэффициент передачи равен 1. Так как датчик уровня является очень быстрым – его постоянная времени очень мала, таким образом его передаточная функция близка к 1. Отсюда следует, что при моделировании системы в пакете MATLAB мы можем пренебречь данным датчиком.

На основании рассчитанных данных смоделируем систему в пакете MATLAB.

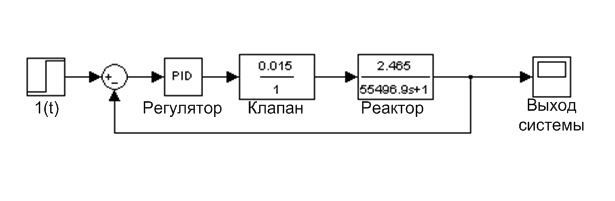
Рис. 3.7. Структурная схема объекта с ПИ-регулятором

Переходный процесс для данной системы будет выглядеть следующим