АКР для линейных дискретных систем. Термокондуктометрические и магнитные газоанализаторы

ТАУ 28-1. АКР для линейных дискретных систем.

Пусть объект будет стационарный: x[(k+1)T] = Ax(kT)+Bu(kT)

Эл-ты матриц А и В постоянные.Х – это отклонение от базовых значений.

Разговор идет об стабилизации системы.

J=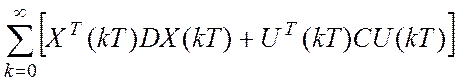 

Поскольку Х – отклонение, то поставим задачу минимизации, т.е. чтоб отклонение было наименьшим.

Введем ф-цию  φ(х(kT)) = min J .  Пусть φ(х(kT)) = Х^Т(кТ)RX(kT)

T и dt – разные значения.

Для дискретн. системы, при условии, что Т очень маленькое (напр. 0.001*t_рег) тогда можно пользоваться методами расчета для непрерывных систем. Но Т большое, поэтому ур-ние Белмана не подходит. Можно записать рекурентное ур-ние, которое будет описывать эффективность работы системы.

Пусть стратегию управления наилучшую подобрали для тактов, начиная со 2-го такта. Не успели найти оптимальное управление на 1-ом такте. Найдем это для 1-го такта:

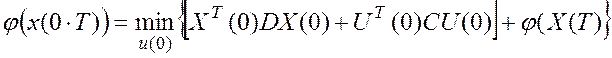
где  - решение для всех остальных тактов.

Остается найти решение для 1-го такта. Т.к. А,В,С,D = const , тогда можно сказать , что решение для 1-го такта будет справ-во и для остальных тактов.

Функцию можно рассмотреть как

ΔХ = Х(Т) – Х(0)

Разложим ф-цию в ряд Тейлора: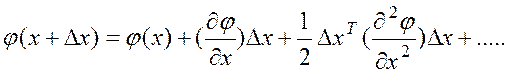

Т.к.  Т будет значительное, тогда Δх будет значительное и поэтому используем и квадратичный член ряда, а остальные будут незначительные. Подставляя, получим:

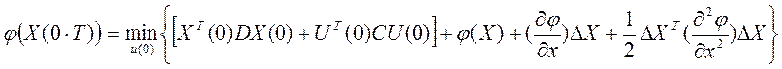Т.к. в составе  в явном виде нету U(0), тогда их можно вынести за скобки и перенести в левый бок и сократить:

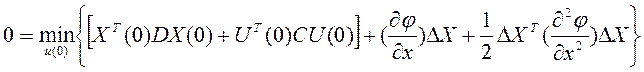
Дальше подставим ΔХ и возьмем производную:

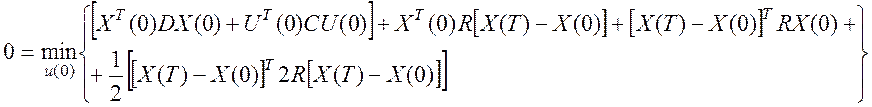
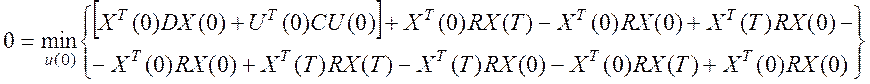
ТАУ 28-2

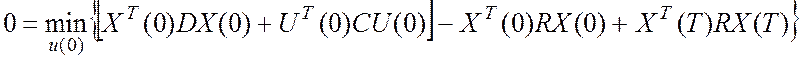
Дальше вместо Х(Т) подставим АХ(0)+ВU(0):

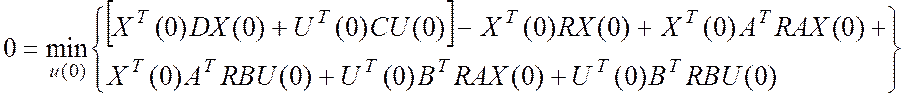Продифференцируем по U(0):     

;

Чтобы найти матрицу R, нужно U_опт(0) подставить в функц-ное ур-ние:

Для этого введем обозначения:   U_опт(0) = M·X(0)

                                                        U_опт(kT) = M·X(kT)

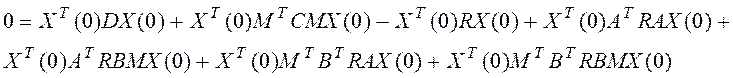
Сократим на  Х^Т(0) и Х(0):  

Получили тяжелое для решения алгебраическое ур-ние.

МОД 28-1Виды активных воздействий для определения динамических характеристик. Изучение объекта и подготовка аппаратуры для проведения эксперимента.

В данном методе используется метод переходных функций.

Переходной функцией h(t) называется зависимость выходной величины y(t) = f(t) при изменении входной величины x₀ до x₀+A.

x₀ – значение входной величины в стационарном режиме, т.е. y = const, y’(0) = 0, y”(0) = 0.

A – амплитуда активного воздействия.

С учетом линейной статической характеристики данного объекта, выбор стационарного режима (x₀ , y₀) не влияет на уравнение динамической модели объекта.

.

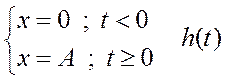Полученная зависимость h(t) аппроксимирует решение соответствующего ДУ.

Если x = δ(t), то

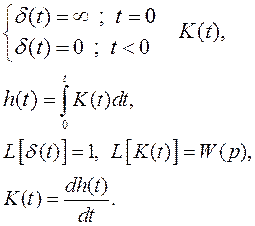
Процесс получения динамической модели подразделяется на следующие при этапа:

1.  изучение свойств модели объекта;

2.  подготовка аппаратуры для измерения координат объекта;

3.  планирование эксперимента по снятию переходной функции.

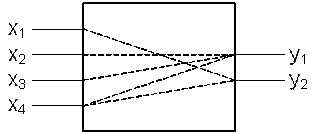1) Изучается технологический режим работы объекта. Проводится анализ модели объекта как объекта управления. Составляется структурная схема.

По записях в журнале, базах данных изучается диапазон измерения.

Далее изучается статистика объекта.

Y₁ = f(X₂, X₃, X₄); Y₂ = f(X₁, X₄)

Y₁ = f(X₂); X₃, X₄ = const

Нужно получить статическую характеристику по каждому каналу.

Если в процессе эксплуатации происходит частичная смена режима работы и при этом X_iи Y_i изменяются в широких пределах, тогда изучается характеристика производного эксперимента.

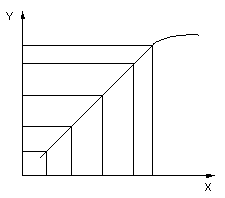Если выходная величина Y_iменьше незначительно Y_i = (0,1 – 0,15)Y₀, то можно считать характер такого объекта линейным или для анализа использовать статические характеристики его подобных.

В области линейного изменения назначается несколько значений (X₀, Y₀).

МОД 28-2Определяется уровень помех и возмущений на данном объекте, и применяются методы их стабилизации.

Если это невозможно сделать, тогда определяется средняя частота их действий, появлений.

2) От точности измерения данных координат зависит точность получения динамической модели.

При наличии входных возмущений, класс точности применяемых приборов должен быть 1,0 – 2,0. Если эксперимент проводится в отсутствии помех, то приборы с классом точности 0,2 – 0,5.

3) Вначале определяется минимальное время проведения данного эксперимента. Если он проводится без помех, то на каждом режиме (X₀, Y₀) происходит снятие 2 – 4 различных значений. Если производится при шумах, то — 8 – 10.

Так же важным этапом при планировании эксперимента является выбор вида возмущающего воздействия и ее амплитуды А.

Некоторые виды возмущающих воздействий и их характеристики приведены в следующей таблице.

Из данной таблицы видно, что каждое воздействие содержит определенный спектр частот, в котором полученное АФХ будет наиболее точным. В частности, при ступенчатом воздействии величина АФХ уменьшится при увеличении ω, поэтому наиболее точным АФХ можно получить в области низких частот. В прямоугольном импульсе наиболее точное значение АФХ можно полечить в следующем частотном методе, приведенном в таблице. Наиболее точные значения при ω₁ = 3/4·π/τ.