






ТАУ 15-1. Синтез системы управления с использованием упредителей Смита.
Пусть объект содержит большое запаздывание. На систему
действует возмущающее воздействие F. Передаточная объекта:![]()
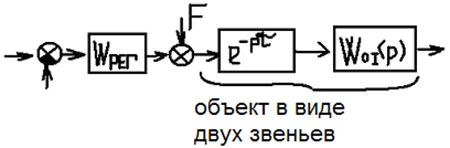
 Сложность – в запаздывании, решение этой задачи
предложил Смит:
Сложность – в запаздывании, решение этой задачи
предложил Смит:
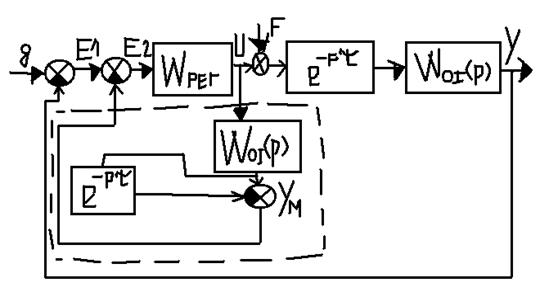
Упредитель Смита – пунктиром.
Имея эту структурную схему, можем попробовать записать связь выхода системы с задающим воздействием и возмущающим.
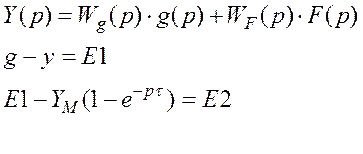 ,
, 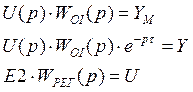
F=0,
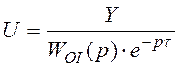 ,
, 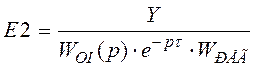 ,
, 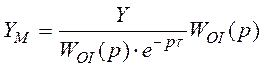
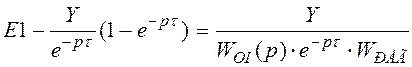
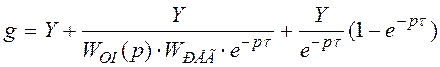
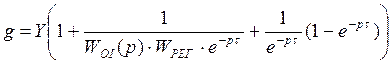
![]()
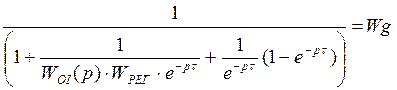
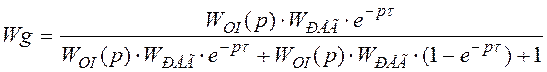
В области тех частот, которые характерны для работы
системы, выполняется условие: пусть ![]() Þ пренебрегаем
единицей:
Þ пренебрегаем
единицей:
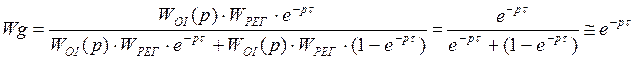
ТАУ 15-2
![]() , получаем вид W –
чистое запаздывание, от него мы не можем избавиться у реального объекта.
, получаем вид W –
чистое запаздывание, от него мы не можем избавиться у реального объекта.
Возьмем задающее воздействие нулевое: F¹0, g=0:
![]()
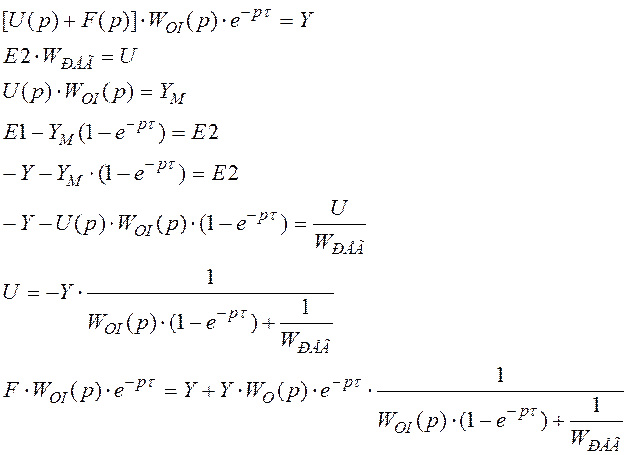
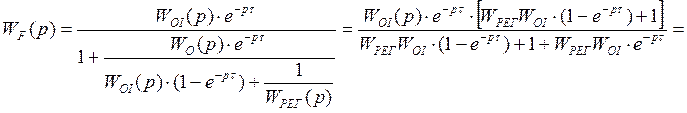
(WРЕГWOI>>1)
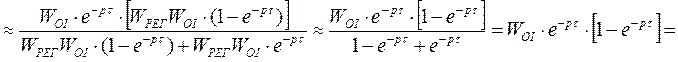
![]()
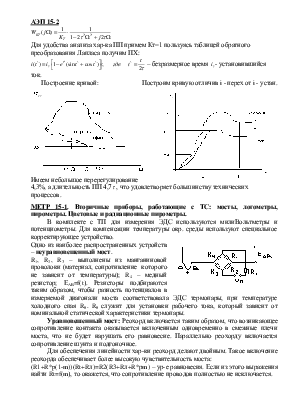
МОД 15-1. Оценка взаимосвязи переменных статистической
модели на основе корреляционного анализа
Ход тэхналапчнага працэсу характарызуецца значэннями фиксаванай колькасщ параметрау, большая частка якіх бесперапынна змяняецца адносна cвaix сярэдних значэнняу. Гэтыя змянении носяць выпадковы характар i называюцца выпадковымі працэсами. Працэсы, статыстычныя характарыстьки яких не змяняюцца у часе, называюцща стацыянарными.
Статыстычныя характарыстыки выпадковага працэсу знаходзяцца шляхам усярэднення значэнняу выпадковых велічынь, якія залежаць ад ардынат працэсу. Такое усярэдненне можа быдь праведзена па часу, калі маецца адна рэалізацыя працэсу, i па мноству для фиксаванага моманту часу, калі маецца мноства незалежных рэалізацый. Выпадковы працэс, для якога выники усярэднення, праведзенага тым или другим спосабам, з'яуляюцца аднолькавымі, мае уласцивасць эргадычнасці (будзем разглядаць стацыянарныя, эргадычныя выпадковыя працэсы).
Сярэдняе значэнне стацыянарнага, эргадычнага працэсу пастаяннае:
М[x(t)] = lim![]()
![]() x{t)dt. (3.2.30)
x{t)dt. (3.2.30)
Пры вылічэнне іншых статыстычных характарыстык выпадковага працэсу звычайна зручна папярэдне цэнтраваць яго, г.зн. адняць ад ардынат працэсу яго сярэдняе значэнне.
Уся неабходная для разликау
линейных систэм статыстычная инфармацыя для стацыянарных працэсау змяшчаецца у ix карэляцыйнай
функцыі, якая разлічваецца па формуле 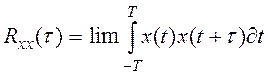 (3.2.30)
(3.2.30)
Фізічна велічыня
карэляцыйнай функцьі для некаторага моманту
![]() паказвае, наколькі
значэнне выпадковага працэсу у момант tзвязана са значэннем, якое адстае ад яго на час
паказвае, наколькі
значэнне выпадковага працэсу у момант tзвязана са значэннем, якое адстае ад яго на час ![]() .
.
3 формулы бачны асноуныя уласцівасщ карэляцыйнай функцьй:
1. Rxx {![]() ) з'яуляецца цотнай функцыяй.
) з'яуляецца цотнай функцыяй.
2.Rхх(О) роуна сярэдняму значэнню квадрата адхілення выпадковага працэсу ад яго матэматычнага чакання i заусёды больш за нуль. Гэту велічыню называюць дысперcияй выпадковага працэсу.
3.![]()
4. Імкнецца да нуля пры ![]() →
→ ![]() .
.
У тых выпадках, калі
даследуецца сувязь паміж двума выпадковьмі працэсамі x(t) и Y(t), характарыстыкай гэтай
сувязі з'яуляецца
узаемакарэляцыйная функцыя 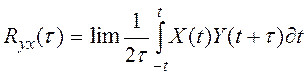 (3.2.32)
(3.2.32)
Велічыня узаемакарэляцыйнай
функцьй паказвае, як залежыць ардыната працэсу y(t) у момант t+![]() ад ардынаты працэсу x(t) у момант t. Асноуныя уласщвасщ
ад ардынаты працэсу x(t) у момант t. Асноуныя уласщвасщ
![]() :
:
1. Rxy(![]() ) = Ryx(-
) = Ryx(-![]() ), Rxy(
), Rxy(![]() ) не з'яуляецца
цотнай функцыяй.
) не з'яуляецца
цотнай функцыяй.
2.Rxy(![]() ) имкнецца да нуля пры
) имкнецца да нуля пры ![]() →0.
→0.
Аутакарэляцыйная функцыя
сигналу f(t), яки уяуляе сабой
суму двух
выпадковых сигналав m(t) i n(i), можа быць выражана
праз карэляцыйныя функцьп складальных: ![]() (3.2.33)
(3.2.33)
Калі n(t) i m(i) не карэляваныя
паміж сабой, то узаемакарэляцыйныя функцьп у (3.2.33) роуны нулю i Rff(![]() ) = Rnn(
) = Rnn(![]() ) + Rmm(
) + Rmm(![]() )- (3.2.34)
)- (3.2.34)
Разлік лінейных сістэм праводзяць з дапамогай пераутварэнняу Фур'е i частотных характарыстык лшейных звёнау. У гэтым выпадку замест карэляцыйных функцый
МОД 15-2
спадручней выкарыстоуваць ix пераутварэнні па Фур'е - спектральную i узаемную спектральную шчыльнасць. Спектральную
шчыльнасць падлічваюць па формуле 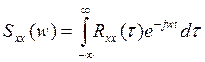 (3.2.35)
(3.2.35)
Яна з'яуляецца цотнай функцыяй w, для любой частаты wSxx(w)> 0- Фізічна велічыня спектральнай шчыльнасщ паказвае, якая доля магутнасщ выпадковага працэсу прыходзщца на гэту частату.
Агульная ж магутнасць
выпадковага працэсу можа быць падличана як интеграл яго спектральнай шчыльнасць
3 адваротнага пераутварэння Фур'е можна
атрымаць 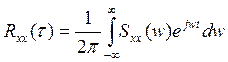 (3.2.36) а дысперсия роуная сумарнай магутнасщ выпадковага працэсу:
(3.2.36) а дысперсия роуная сумарнай магутнасщ выпадковага працэсу: 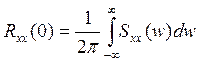 (3.2.37)
(3.2.37)
Пераутварэнне Фур'е узаемнай карэляцыйнай
функцыі называецца узаемнай спектральнай шчыльнасцю. 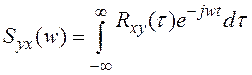 (3.2.38). Яна не з'яуляецца цотнай функцыяй частаты i мае уласцівасць
(3.2.38). Яна не з'яуляецца цотнай функцыяй частаты i мае уласцівасць ![]()
Пры праходжанні выпадковага сигналу праз линейнуюcистему яго характарыстыю змяняюцца. Формулы сувязі памиж характарыстыкамі сістэмы i характарыстыкамі cигналy на яе входе i выхадзе асабліва простыя, калі карыстацца спектральнымі шчыльнасцямі выпадковых працэсау i частотнымі хара-мі сістэмы.
Няхай x(t) i y(t) - адпаведна
выпадковыя працэсы на уваходзе i выхадзе сктэмы з амплітудна-фазавай характарыстыкай
W(jw), тады ![]() (3.2.39)
(3.2.39)
Сярэдняе значэнне квадрата cигналу на уваходзе сктэмы у адпаведнасци з (3.2.37) можа быць вылічана па формуле
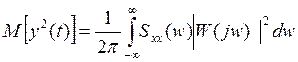 (3.2.40)
(3.2.40)
У тым выпадку, кaлi Sx (w) i W(jw) - рацыянальныя функцыі, інтэграл (3.2.40) можа быць разлічаны з дапамогай табліц.
Узаемная спектральная шчыльнасць працэсау на уваходзе линейнай
систэмы звязана са спектральнай шчыльнасцю працэсу на уваходзе i частотнай характарыстыкай
сістэмы выразам ![]() (3.2.41)
(3.2.41)
Выраз (3.2.41) адпавядае сувязі паміж узаемнай
карэляцыйнай функцыяй сигналау на уваходзе i выхадзе аб'екта,
карэляцыйнай функцыяй уваходнага синалу и импульснай характарыстыкай аб'екта: 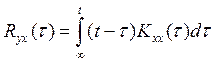 (3.2.42)
(3.2.42)
Урауненні (3.2.41) i (3.2.42) з'яуляюцца асновай для вызначэння дынамичных характарыстык аб'екта статыстычнымі метадамі.
АЭП 15-1. Синтез регулятора тока в системе с подчиненным регулированием
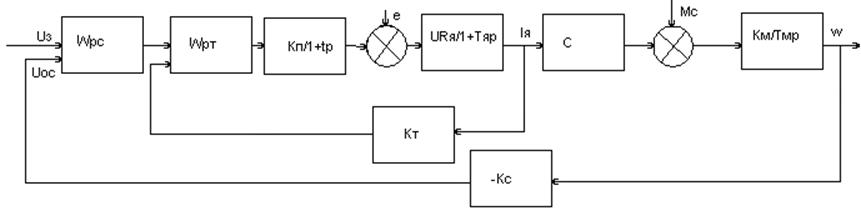
Структ-я схема
Обычно пренебрегают внутренней ОС по ЭДС т.к инерционность электромагнитная и механи-я двигателя больше инерционности преобразователя. Условия:
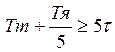
Для контура тока W объекта токового контура
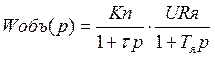
Обычно Тя больше Тау , тогда считаем Тя большая , а тау-малая инерционность. Задача регулятора – скомпенсировать большую постоянную времени. Применяют Пи-регулятор тока с передаточной функцией
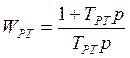
Примем что инерционность Трт=Тя тогда разомкнутый контур тока
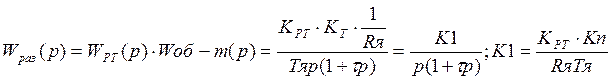
Для зам-го контура:
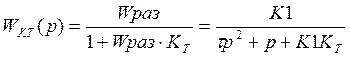
Для удобства анализа приведем к конической форме:
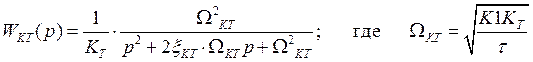 -резонан-я
частота, а
-резонан-я
частота, а 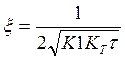 – коэф-т демпфирования.
– коэф-т демпфирования.
Характер ПП определяется ![]() . Рекомендуют
. Рекомендуют ![]() =1 тогда
ПП – апериодический. Обычно выбирают
=1 тогда
ПП – апериодический. Обычно выбирают ![]() =1/
=1/![]() =0,707, тогда
=0,707, тогда 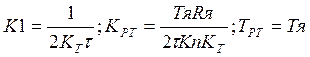 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.