



 ТАУ 14-1.
Синтез систем управления методом расчета параметров регулятора на желаемый
показатель колебательности.
ТАУ 14-1.
Синтез систем управления методом расчета параметров регулятора на желаемый
показатель колебательности.
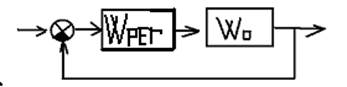
ПИ-регулятор: Задаемся WРЕГ. j=arcSin(1/MЖЕЛ). Имеем систему вида:
 Передаточная ПИ-регулятора имеет вид:
Передаточная ПИ-регулятора имеет вид: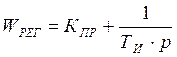 .
.
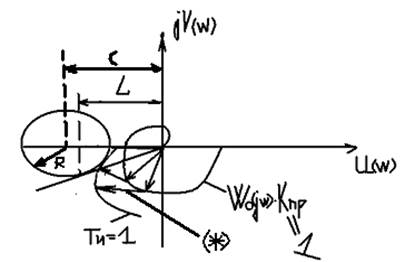
Строим АФЧХ, при КПР=1 для построения интегральной составляющей:
Здесь окружность строится:
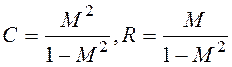
Где L=1/KПР.РАСЧ.. Зададимся численными значениями ТИ=1;5;10;100;…
Строим один график для КПР=1, ТИ=5 и т.д.Þполучим семейство кривых, причем
1/ТИjw=-j(1/ ТИw).
Знак минус означает поворот по часовой стрелке(*). Задаемся частотами w [w1, w2, …wn], находим 1/ ТИwi. Получим новую кривую, проводим окружностьÞполучаем LÞ KПР.РАСЧ=1/ L. Составляем таблицу:
|
ТИ |
1 |
5 |
10 |
100 |
|
|
KПР.РАСЧ |
Строим график
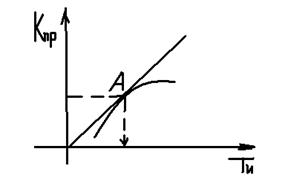
Точка А является лучшим вариантом.
Передаточная ПИД-регулятора вида: 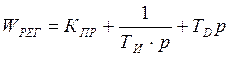 .
.
Зададим:
|
ТИ |
1 |
5 |
10 |
100 |
|
|
ТD |
0,5 |
5 |
6 |
20 |
|
Строим АФЧХ, при КПР=1, интегральная составляющая –j(1/ТИwi), дифференциальная составляющая jТDwi. Тогда в силу –j(1/ТИwi)+ jТDwi при построении вектор –j(1/ТИwi) поворачиваем по часовой на 900 и jТDwi на 900 против часовой стрелки, получим суммарный вектор j(-1/ТИwi+ТDwi):
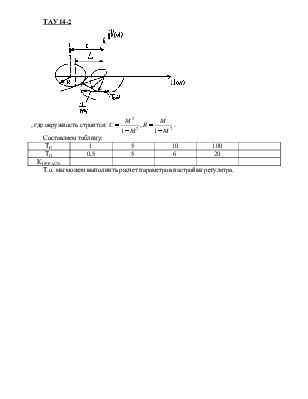
ТАУ 14-2
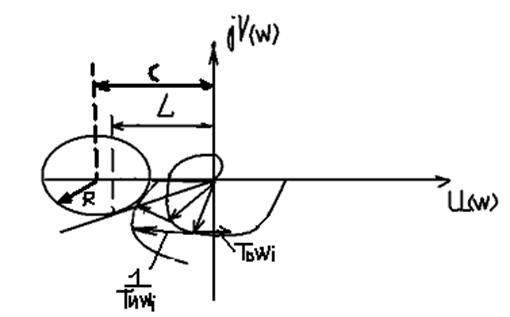
,
где окружность строится: 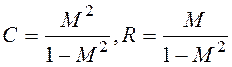 .
.
Составляем таблицу:
|
ТИ |
1 |
5 |
10 |
100 |
|
|
ТD |
0,5 |
5 |
6 |
20 |
|
|
КПР.РАСЧ. |
Т.о. мы можем выполнить расчет параметров настройки регулятра.
МОД 14. Принципы построения матмоделей аналитическими методами.
Обобщённое уравнение материального баланса для некоторых ХТП имеет вид: Приток вещества – расход вещества = накопление вещества ∆М=∫[Iвх(t)-Iвых(t)]dt, где Iвх(t),Iвых(t)-входной и выходной потоки вещества. Это уравнение описывает нестационар. условие протекания ХТП. Для стационарных условий: Приток вещества= расход вещества Iвх(t)=Iвых(t)
Обобщённое уравнение теплового баланса: Приток тепла – расход тепла = накопление тепла ∆Q=∫[Qвх(t)-Qвых(t)]dt, где Qвх(t),Qвых(t)-входной и выходной тепловой поток. В стационарном режиме уравнение теплового баланса: Приход тепла = расход тепла Qвх(t)=Qвых(t).
Соотношения описывают в основном макрокинетику, т.е. элементарные процессы гидродинамики. В зависимости от особенностей макрокинетики применяются различные ур-я, структуры для получения детерминированных моделей:
1) конечное уравнение применяется для описания стационарных режимов.
2) Обыкновенные ДУ и их системы. Могут быть линейными и нелинейными. Описывают нестационарные режимы работы ХТП.
3) ДУ в частных производных и их системы. Описывают нестационарные режимы работы ХТП с распределёнными параметрами.
|
![]() 1) Модель
идеального перемешивания;
1) Модель
идеального перемешивания;
2) Модель идеального вытеснения.
3) Диффузионная;
4) Ячеечная; 5) Комбинированная.
Универсальным видом типовой модели гидродинамики является ДУ, которое описывает зависимость концентрации вещества в потоке, функции времени, пространственных координат.
К типовым моделям гидродинамики предъявляются следующие требования:
1) Они должны давать возможность рассчитать коэффициенты для различных гидродинамических режимов;
2) По данным уравнениям необходимо проводить исследования гидродинамического процесса и оптимизацию.
Если в ХТП присутствуют несколько потоков веществ, то для каждого потока – отдельная модель гидродинамики. При матем. описании гидродинамики сложных ХТП необходимо упрощать его свойства (структуру ХТП), но с сохранением его свойств и подбирать к данной структуре соответствующую типовую модель гидродинамики, математической описание которой уже известно (за исключением численных значений коэффициентов).
АЭП 14. Регуляторы CАУ ЭП
В ЭП в основном применяют стандартные регуляторы, выполненные на базе ОУ. ОУ имеют несколько каскадов усиления: входной дифференциальный каскад имеет 2 входа: инверт. и неинверт. На инверт. входе ↑ сигнала на входе приводит к ↓ выходного сигнала. На неинверт. – наоборот. ОУ имеет высокое вх. сопрот. Внутренние каскады обеспечивают промежуточное усиление. Выходной каскад – эммитерный повторитель. Он обеспечивает малое выходное сопрот. Кu – коэффициент усиления (103 ÷ 106). Необходима коррекция частотных характеристик, т.к. возможны автоколебания, когда ОУ охватываются ОС. Цепи коррекции индивидуальны. Применяются схемы компенсации уровня выходного сигнала. Регуляторы ЭП строят на основе ОУ, охватываемых ОС. Наибольшее применение нашли следующие регуляторы:
П-регулятор. ОС –жесткая.
R1

 W(p)=kп
W(p)=kп
Kп=R1/R0
В пределах полосы пропускания ЭП ЛАЧХ регулятора – прямая линия.
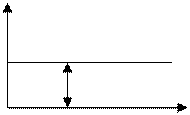
L
20 lgkp
ПИ-регулятор представляет собой союз П и И регулятор.
R1 C1
 |
W(p)=kп(1+pT1)/pT1
kп=R1/R0; T1=R1C1
ПИД-регулятор выполняет одновременно действие 3-х регуляторов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.