Практическое занятие 5
Нахождение экстремума функции методом дихотомии
1. Цель и порядок выполнения работы
Цель работы - моделирование на ЭВМ одного из методов нахождения экстремума функции (метода дихотомии) и исследование на модели заданной функции.
Порядок выполнения работы:
- ознакомиться с описанием работы;
- разработать форму (в EXCEL) реализующую этот метод;
- заполнить форму и отладить её;
- исследовать заданную функцию;
2. Общие сведения
Суть метода дихотомии состоит в следующем. Если разделить заданный диапазон изменения функции, в котором отыскивается её экстремум, пополам, определить, в какой половинке находится экстремум, затем эту половинку поделить снова пополам, снова определить, в какой половинке находится экстремум и т.д., то в итоге этих повторяющихся действий мы попадем в точку экстремума. Но, очевидно, этот процесс деления бесконечен, так как точка по протяженности - бесконечно малая величина. Следовательно, конечность вычислительного процесса по методу дихотомии может быть достигнута, если задастся допустимой погрешностью (Е) вычисления координат точки экстремума. Поэтому алгоритм нахождения экстремума функции сводится к следующему.
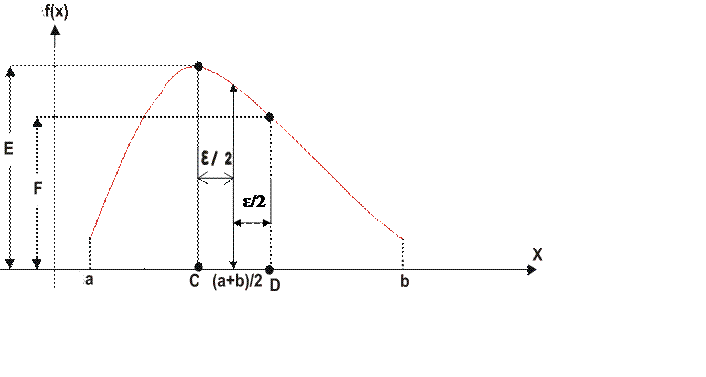
Пусть требуется найти максимум функции y =f(x ) в диапазоне изменения её аргумента от а до b с погрешностью +(-) Е по координате x (рис. 1.1). Прежде всего, следует проверить условие |b-a|<2 E. Если оно выполняется, то в пределах заданной погрешности мы уже находимся в "точки" экстремума. Если нет, то вычисляем две точки на оси x, находящиеся на расстоянии +E /2 от середины отрезка ab.
![]()
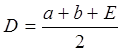
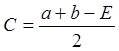
Р
Рис. 1.1
Вычисление ординат этих точек необходимо для того, чтобы определить, в какой половине отрезка ab находится максимум функции.
Для этого вычисляем значения функции при x=C и x=D. Получим соответственно E=f(C) F=f(D).Теперь сравним значения E и F. Если E>F, то это значит, что максимум функции находится в левой половине отрезка ab, и мы "отбрасываем" правую половинку, т.е. "перемещаем" точку в точку D: b=D. Если условие не выполняется, то максимум находится в правой половине отрезка и производится перемещение точки а в точку C: а=C.
Далее перечисленные действия, начиная с проверки первого условия повторяются до тех пор, пока первое условие не будет выполнено. Это означает, что в пределах погрешности +E максимум достигнут. После чего производится выполнение функции в точке максимума
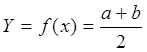
Для того, чтобы найти минимум функции, нужно условие E>F заменить условием F>E. Все остальные действия сохраняются.
3. Задание
3.1. Разработать метод (в EXCEL) для нахождения max и min функции по методу дихотомии с допустимой погрешностью E = 0,05. Помимо определения координат экстремумов программа должна выводить на экран дисплея с заданным шагом таблицу значений функции и её график.
3.2. Варианты заданий
|
№ варианта |
Функция |
Диапазон изменения аргумента |
Шаг изменения аргумента |
|
1 |
y=2+Sinx |
0<x<2Pi |
x=0,5 |
|
2 |
y=2+Cosx |
-- |
-- |
|
3 |
y=1+Sinx |
-- |
-- |
|
4 |
y=1+Cosx |
-- |
-- |
|
5 |
y=10+5Sinx |
-- |
-- |
|
6 |
y=6+5Sinx |
-- |
-- |
|
7 |
y=7+5Sinx |
-- |
-- |
|
8 |
y=8+6Sinx |
-- |
-- |
|
9 |
y=7+4Sin |
-- |
-- |
|
10 |
y=21+19Sinx |
-- |
-- |
|
11 |
y=3+Cosx |
-- |
-- |
|
12 |
y=6+3Cosx |
-- |
-- |
|
13 |
y=x+Cosx |
-- |
-- |
|
14 |
y=2x+Cosx+1 |
-- |
-- |
|
15 |
y=0,5x+Cosx+1 |
-- |
-- |
|
16 |
y=2/x+2x |
0,1<x<2 |
x=0,2 |
|
17 |
y=1/x+x |
-- |
-- |
|
18 |
y=2/x+x |
-- |
-- |
|
19 |
y=2/3x+3x |
-- |
-- |
|
20 |
y=1/4+4x+1 |
-- |
-- |
|
21 |
y=1/x+5x |
-- |
-- |
|
22 |
y=1/x+1-e |
-- |
-- |
|
23 |
y=1/2x+3-e |
-- |
-- |
|
24 |
y=1/5x+x-1 |
-- |
-- |
|
25 |
y=1-e+1/x |
-- |
-- |
|
26 |
y=2-e+1/2x |
-- |
-- |
|
27 |
y=1/3x+x+2 |
-- |
-- |
|
28 |
y=0,1x-2x+10 |
0,1<x<2 |
x=0,2 |
|
29 |
y=1/5x+5x |
-- |
-- |
|
30 |
y=3/5x+8x |
-- |
-- |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.