Синтез непрерывной системы управления

координат касательную кривой, и в точке касания получим оптимальные значения k и Ти, при подстановке которых в передаточную функцию АФЧХ разомкнутой системы касается окружности с заданным показателем колебательности.

1.3 Расчёт регулятора по каналу управления.

Моделирование работы системы с регулятором

Передаточная функция объекта выглядит следующим образом:

Рисунок 1.1 – структура заданного объекта

Реакция системы на единичное входное воздействие:

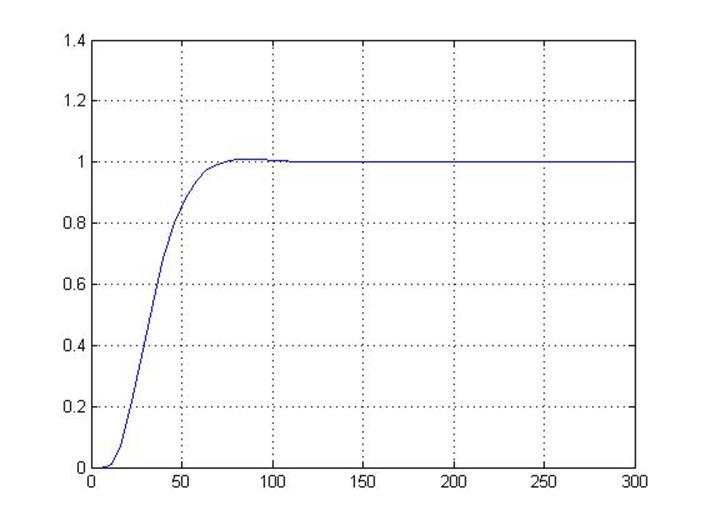
Рисунок 1.2 – реакция объекта на единичное входное воздействие

1.3.1 Расчет П-регулятора

Рассмотрим синтез П-регулятора как наиболее простого.

Программа в среде MATLAB:

clc

clear all

W1=tf([0.95],[7 1]);

W2=tf([1.1],[150 20 1],'td',7);

Wo=W1*W2

% задаем величину показателя качества

M=1.17;

w=-2:0.01:2;

p=j*w;

C0=1.18;

Wo=1.*exp(-7.*p)./(1050.*p.^3+290.*p.^2+27.*p+1);

Wr=C0;

Ws=Wr.*Wo;

% создаем функции для перехода в комплексную область

Re=real(Ws);

Im=imag(Ws);

% объявляем радиус окружности

R=M/(1-M^2);

R=abs(R);

% C - расстояние от мнимой оси до центра окружности

C=M^2/(1-M^2);

x=-R^2:0.01:R^2;

y1=sqrt(R^2-(x-C).^2);

y2=-sqrt(R^2-(x-C).^2);

% k - тангенс угла наклона касательной к окружности

k=tan(asin(1/M));

% задаем уравнение прямой

y3=k*(x);

figure(1);

plot(Re, Im, x, y1, x, y2, x, y3);

axis([-2 2 -2 2]);

grid on

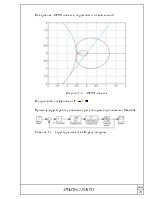
Построение АФЧХ объекта, окружности и касательной

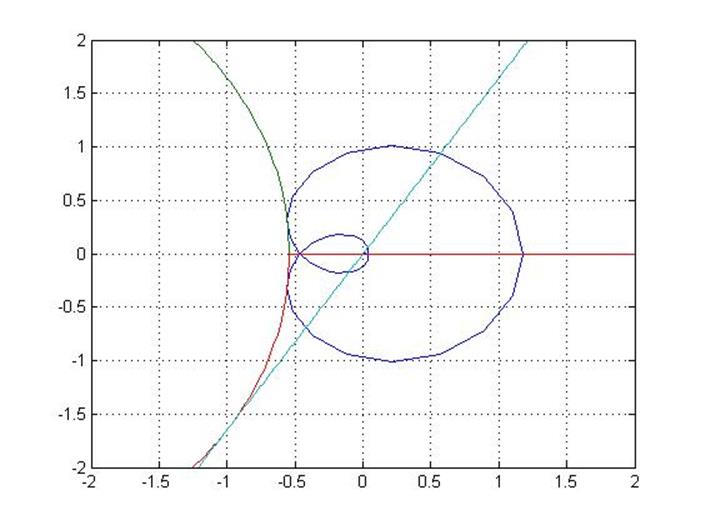
Рисунок 1.3 – АФЧХ объекта

Полученный коэффициент

Промоделируем работу системы с регулятором в приложении Simulink:

Рисунок 1.4 – структура объекта с П-регулятором

График переходного процесса выглядит следующим образом:

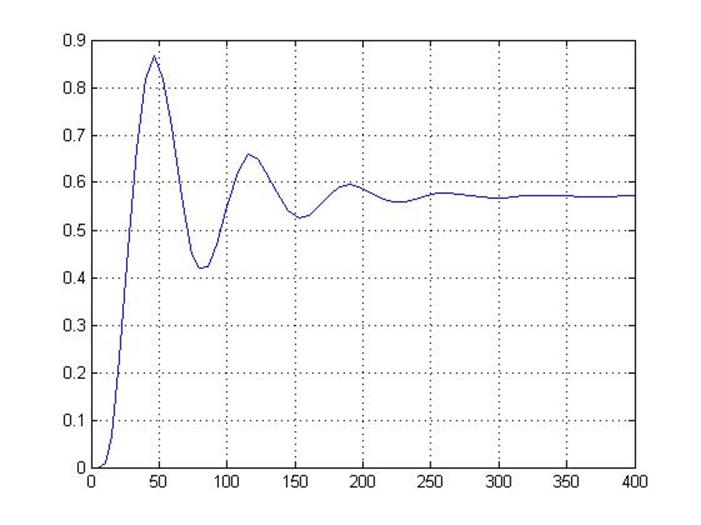
Рисунок 1.5 – переходная характеристика объекта с П-регулятором

В результате чего система достигает перерегулирования σ = 42 %, а установившаяся ошибка превышает ε ≤ 1 %, что удовлетворяет условию курсового проекта. Расчётное время входа системы в допустимые пределы установившейся ошибки – 160 секунда.

Следовательно, P-регулятор не может быть использован.

1.3.2 Расчет ПИ-регулятора

Рассмотрим синтез ПИ-регулятора.

Программа в среде MATLAB:

clc, clear

% задаем величину показателя качества

M=1.17;

w=-2:0.01:2;

p=j*w;

C0=0.13;

C1=32.2;

Wo=1.*exp(-7.*p)./(1050.*p.^3+290.*p.^2+27.*p+1);

Wr=(C0+C1./p);

Ws=Wr.*Wo;

% создаем функции для перехода в комплексную область

Re=real(Ws);

Im=imag(Ws);

% объявляем радиус окружности

R=M/(1-M^2);

R=abs(R);

% C - расстояние от мнимой оси до центра окружности

C=M^2/(1-M^2);

x=-R^2:0.01:R^2;

y1=sqrt(R^2-(x-C).^2);

y2=-sqrt(R^2-(x-C).^2);

% k - тангенс угла наклона касательной к окружности

k=tan(asin(1/M));

% задаем уравнение прямой

y3=k*(x);

figure(1);

plot(Re, Im, x, y1, x, y2, x, y3);

axis([-5 5 -5 5]);

grid on

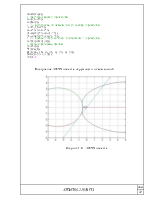
Построение АФЧХ объекта, окружности и касательной

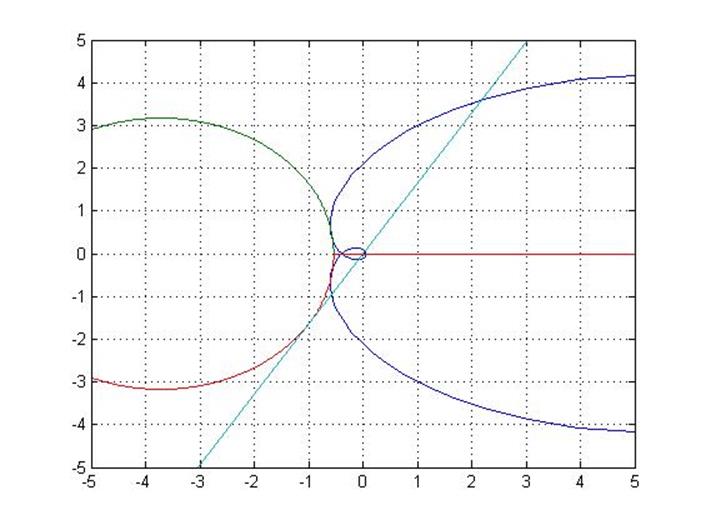
Рисунок 1.6 – АФЧХ объекта

C0=[0.01 0.05 0.08 0.12 0.13 0.12];

C1=[36.8 35.5 34.8 33.6 32.2 31.5];

kp=C0;

Ti=C1;

figure(2)

plot(kp,Ti)

grid on

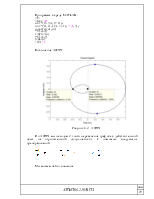
Расчет коэффициентов регулятора:

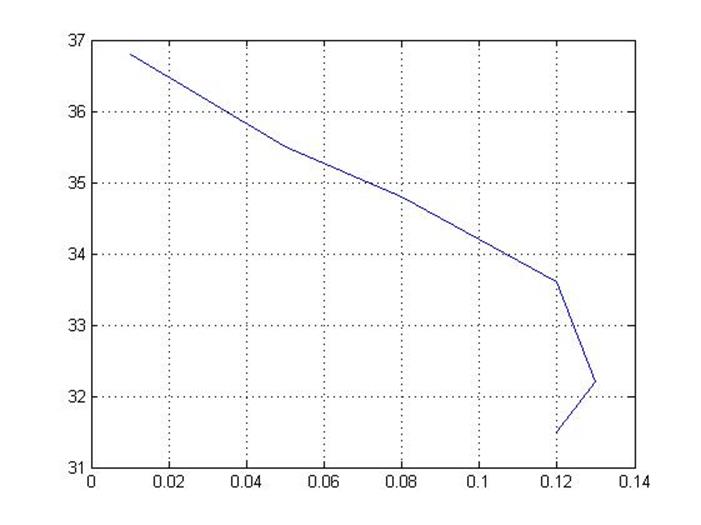
Рисунок 1.7 – нахождение коэффициентов регулятора

Полученные коэффициент

Промоделируем работу системы с регулятором в приложении Simulink:

Рисунок 1.8 – структура объекта с ПИ-регулятором

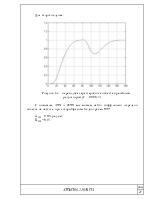
График переходного процесса выглядит следующим образом:

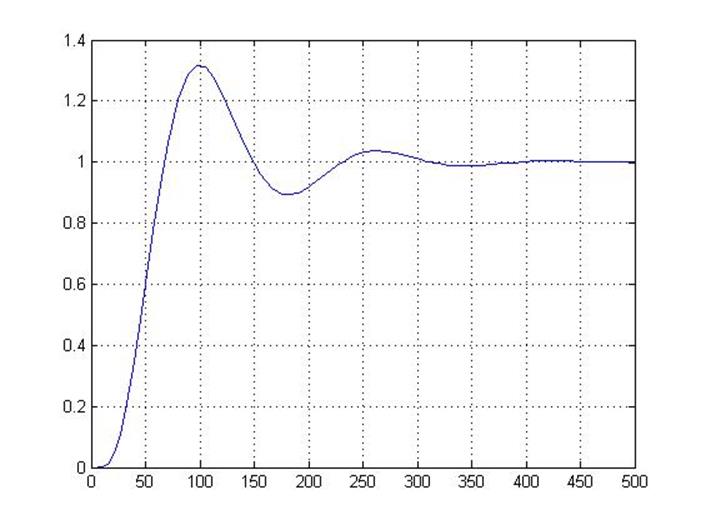
Рисунок 1.9 – переходная характеристика объекта с ПИ-регулятором

В результате чего система достигает перерегулирования σ = 25 %, а установившаяся ошибка не превышает ε ≤ 1 %, что удовлетворяет условию курсового проекта. Расчётное время входа системы в допустимые пределы установившейся ошибки – 212 секунд.

2 Расчет компенсатора возмущающего воздействия

2.1 Основные понятия

Синтез системы комбинированного регулирования может происходить по частям. Сначала необходимо выполнить синтез замкнутого контура регулирования. Что и было сделано в предыдущей части. Затем необходимо рассчитать компенсирующую цепь: определить чувствительный элемент для изменения возмущения; определить точку включения этой цепи в замкнутый контур; составить условие инвариантности; определить вид и параметры передаточной функции цепи, и элементы для физической реализации цепи.

Компенсирующая цепь включает чувствительный элемент для измерения возмущения и элемент, который создаёт необходимый компенсирующий сигнал. Условием инвариантности регулируемой величины Y от возмущения f является равенство, которое возвращает в ноль передаточную функцию W_F .

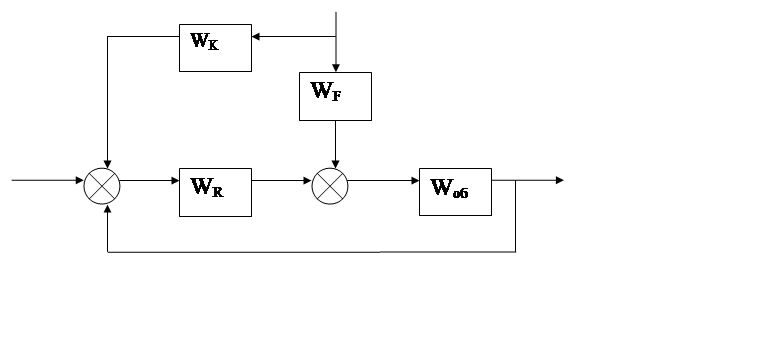
Рисунок 2.1 –схема включения компенсотора

На основании структурной схемы можно записать условие компенсации возмущения:

F*W_F – F*W_K*W_R = 0

Откуда видно, что W_F  = W_K*W_R

Тогда W_K = W_F / W_R.

При условии физической реализуемости этого выражения система обеспечивает полную инвариантность выходного сигнала y от возмущения f.

Если расчётная передаточная функция компенсатора физически не реализуется, то необходимо разложить её в ряд:

W_K (р) = С0 + С1*р + С2*р² + …

И ограничиться приведёнными тремя составляющими. В этом случае система будет иметь частичную инвариантность.

2.2 Расчёт передаточной функции компенсатора. Моделирование работы системы с компенсатором

Передаточная функция :

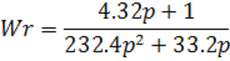
Передаточная функция возмущения:

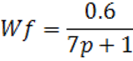
Тогда передаточная функция компенсатора будет равна:

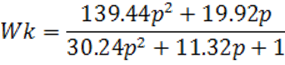
Промоделируем работу системы с данным компенсатором:

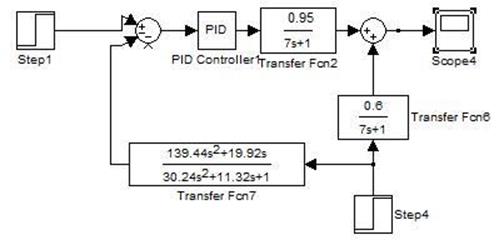
Рисунок 2.2 – структурная схема системы с компенсатором

График переходного процесса по каналу возмущения:

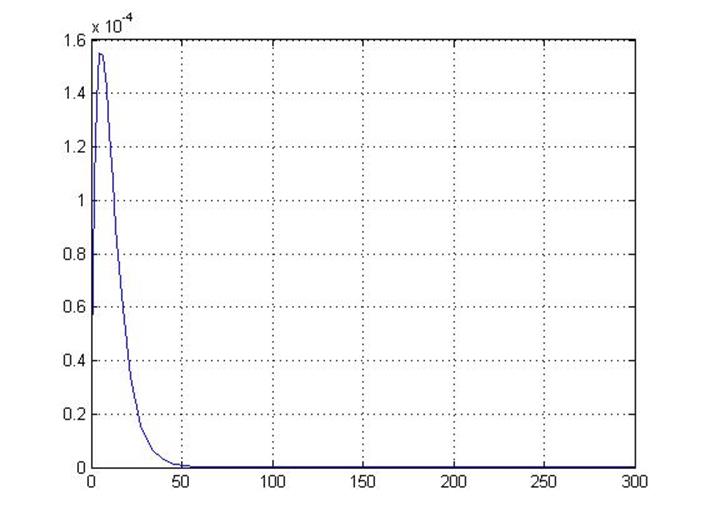
Рисунок 2.3 - переходная характеристика объекта с компенсатором по каналу возмущения

Рассчитанный компенсатор полностью удовлетворяет условию, так как отклонение по каналу возмущения меньше заданного ε ≤ 1 %.

3 Моделирование работы системы с использованием двухпозиционного релейного регулятора

3.1 Вывод характеристики для идеального двухпозиционного реле

3.2 Расчёт параметров автоколебаний. Моделирование работы системы с двухпозиционным релейным регулятором

Система с релейным регулятором имеет вид:

Рисунок 3.1 – структура объекта с релейным регулятором

Построим амплитудочастотную и фазочастотную характеристики. Также построим АФЧХ для данной системы.

Программа в среде MATLAB:

clc

clear all

W1=tf([0.95],[7 1]);

W2=tf([1.1],[150 20 1],'td',7);

W=series(W1,W2)

figure(1)

nyquist(W)

figure(2)

bode(W)

grid on

Построение АФЧХ:

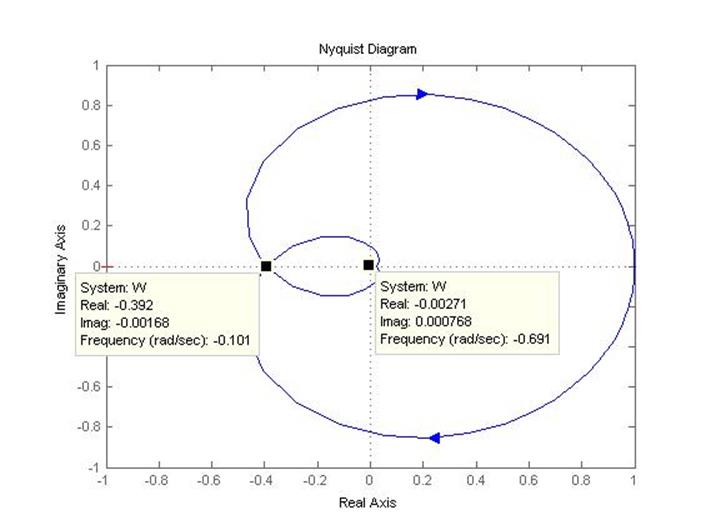
Рисунок 3.2 - АФЧХ

По АФЧХ мы находим 2 точки пересечения графика с действительной осью на отрицательной полуплоскости. С помощью следующих преобразований:

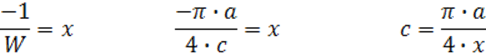
Мы можем найти значения:

С1=0.32  и  С2= 0.0022

При подстановке значений найденных при помощи АФЧХ мы получим следующие виды переходных характеристик системы:

Для первого случая:

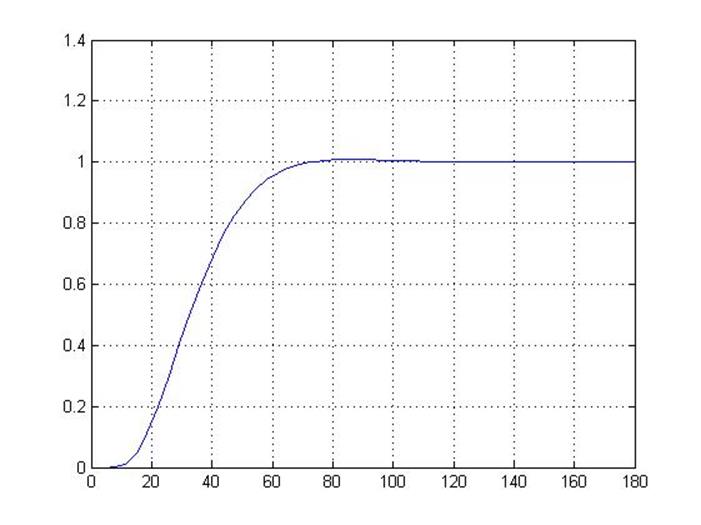
Рисунок 3.3 – переходная характеристика объекта с релейным регулятором (С = 0.32)

Для второго случая:

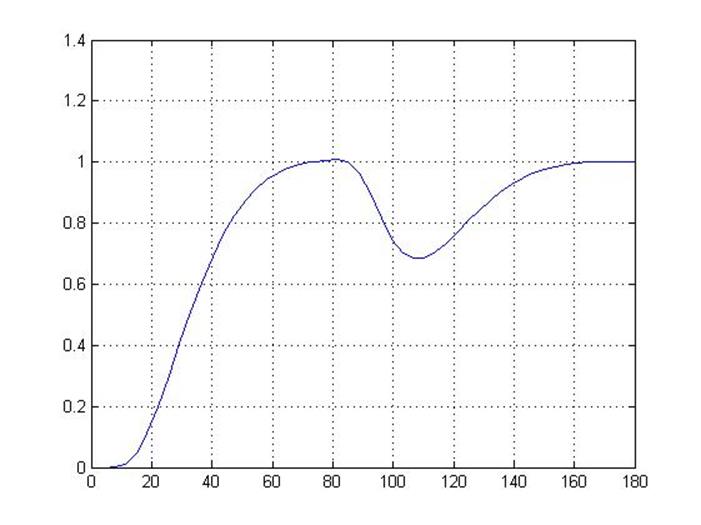
Рисунок 3.4 – переходная характеристика объекта с релейным регулятором (С = 0.00147)

С помощью АЧХ и ФЧХ мы можем найти коэффициент передачи объекта на частоте, при которой фазовый сдвиг равен 180º.

w₁₈₀ = 0.104 рад/сек.

K₁₈₀ = 9.15

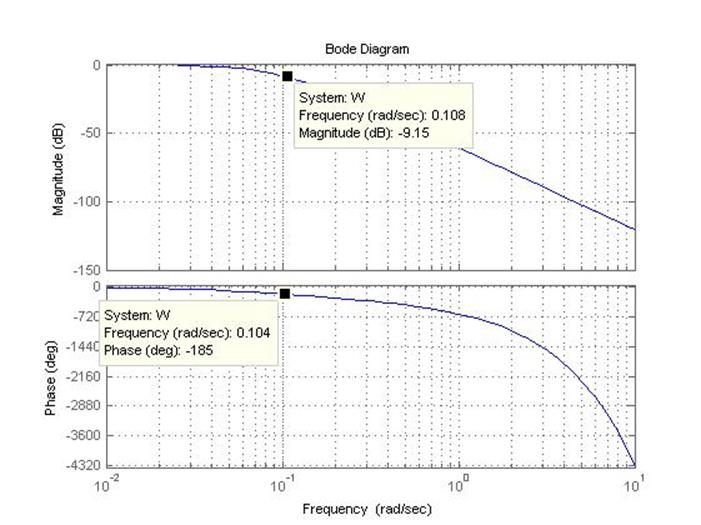
Рисунок 3.5 – АЧХ и ФЧХ

Тогда из формулы:

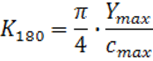
Мы можем выразить значение , которое будет равно:

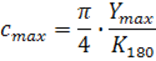
Тогда переходный процесс будет выглядеть следующим образом:

Рисунок 3.6 – переходная характеристика объекта с релейным регулятором (С = 0.0858)

Проанализировав 3 переходные характеристики можно сделать вывод, что при С = 0.0022 система является неустойчивой, при значении С = 0.0858 установившаяся ошибка не превышает ε ≤ 1 %, что удовлетворяет условию курсового проекта, а расчётное время входа системы в допустимые пределы установившейся ошибки – 61 секунда.

Заключение

Для заданной  в условии курсового проекта системы был рассчитан П-регулятор, параметры которого Кп = 1.18. В результате подачи на вход системы единичного воздействия перерегулирование составляет