Расчет изотермического химического реактора с непрерывным перемешиванием.
Весьма существенным при анализе систем
управления является понятие управляемости. Неформально система
управляема, если найдется такое управление ![]() ,
которое обеспечивает ее перевод из произвольного начального состояния
,
которое обеспечивает ее перевод из произвольного начального состояния ![]() в произвольное же состояние
в произвольное же состояние ![]() за конечное время. Более строго
определение управляемости может быть сформулировано следующим образом.
за конечное время. Более строго
определение управляемости может быть сформулировано следующим образом.
Система называется полностью
управляемой , если из любого начального состояния ![]() она
может быть переведена в любое наперед заданное состояние
она
может быть переведена в любое наперед заданное состояние ![]() с помощью некоторого управления
с помощью некоторого управления ![]() за конечное
за конечное ![]() .
.
Возможен случай частично управляемой системы, т.е. системы, имеющей подмножества начальных состояний, из которых достижение произвольного желаемого состояния за конечное время невозможно.
Рассмотрим случай, когда имеется
изотермический химический реактор с перемешиванием реагентов, в котором
происходит необратимая реакция ![]() , где реакция
, где реакция ![]() имеет порядок 2, а реакция
имеет порядок 2, а реакция ![]() ¾ порядок ½. Причем
скорости реакций заданы: r1 = k1cA, r2 = k3cB, где k1, k3 ¾ константы скоростей реакций.
¾ порядок ½. Причем
скорости реакций заданы: r1 = k1cA, r2 = k3cB, где k1, k3 ¾ константы скоростей реакций.
Модель процесса в этом случае задается следующими уравнениями:
![]() ,
,
![]() .
.
Требуется поддержать сА и сB
как можно ближе к заданным уставкам сАd и сAd
, изменяя концентрации реагентов ![]() и
и ![]() , т.е. cAf и
сBf .
, т.е. cAf и
сBf .
После введения безразмерных переменных
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
приводится к виду:
![]() ,
, ![]() (1)
(1)
![]() ,
,
![]() . (2)
. (2)
Тогда задача регулирования формулируется
так: поддерживать выходные концентрации ![]() на
заданных уровнях, изменяя входные концентрации
на
заданных уровнях, изменяя входные концентрации ![]() .
.
Таким образом, имеем нелинейную систему, которая записана в виде системы 2-ух дифференциальных уравнений 1-го порядка :
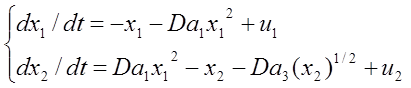
Синтезируем нашу нелинейную систему методом обратных задач.
Метод обратных задач используется тогда, когда зная конечный результат, делаем расчет, находим уравнения, формулы и т.д., т.е. находим оптимальное управление для нашей системы.
Для нашего случая на выходе должна быть желаемая динамическая характеристика.
Сведем систему уравнений до уравнения
самого высокого порядка. Для этого продифференцируем ![]() по
времени :
по
времени :
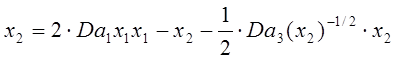 (3)
(3)
Зададимся желаемым ДУ 2-го порядка :
![]()
Возьмем, что от системы управления требуется, чтобы ее переходная характеристика как можно быстрее стремилась к установившемуся значению с минимальным перерегулированием. Системы такого типа принято называть системами с апериодической реакцией. В качестве меры близости переходной характеристики к установившемуся значению принимают зону, равную 2% от этого значения. Тогда временем установления считают время Ts, за которое переходная характеристика входит в указанную зону. Апериодическая реакция характеризуется следующими показателями:
1. Установившаяся ошибка = 0.
2. Быстродействие ® минимальное время нарастания и время установления.
3. 0,1% £ относительное перерегулирование < 2%.
4. Относительный выброс ниже установившегося значения < 2%.
Показатели (3) и (4) требуют, чтобы после того как в момент Ts переходная характеристика войдет в зону 2% от установившегося значения, она все время оставалась в пределах этой зоны.
Чтобы определить коэффициенты передаточной функции замкнутой системы T(s), при которых реакция будет иметь апериодический характер, приведем сначала эту передаточную функцию к нормированному виду.
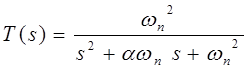 (4)
(4)
Разделим числитель и
знаменатель на ![]() :
:
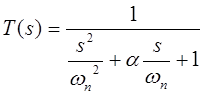 (5)
(5)
Введя обозначение ![]() , получим:
, получим:
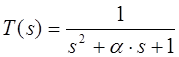 . (6)
. (6)
Выражение (3) ¾ это нормированная передаточная функция
замкнутой системы второго порядка. Тем же самым способом определяются и
нормированные передаточные функции систем более высокого порядка. Коэффициентам
a,b,g и т.д.
придаются значения, при которых система будет иметь апериодическую реакцию. В
выражении (3) фигурирует нормированная переменная ![]() .
Поэтому частота
.
Поэтому частота ![]() определяется по заданному времени
установления или времени нарастания. Так, если в системе второго порядка
необходимо иметь время установления, равное 1с, то мы имеем нормированное время
установления
определяется по заданному времени
установления или времени нарастания. Так, если в системе второго порядка
необходимо иметь время установления, равное 1с, то мы имеем нормированное время
установления
![]() .
.
Отсюда находим частоту ![]() :
:
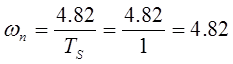 .
.
После этого можно записать передаточную функцию замкнутой системы в виде (4):
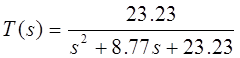
Промоделируем полученную систему, используя приложение к математическому пакету MATLAB-Simulink:
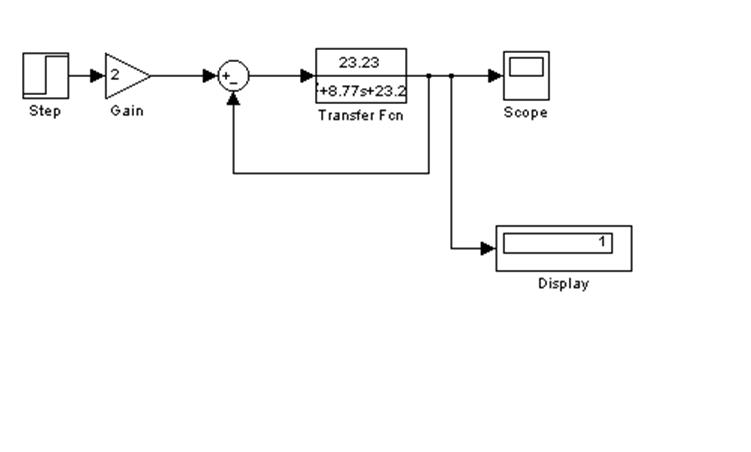
Переходной процесс для нашей системы выглядит следующим образом:
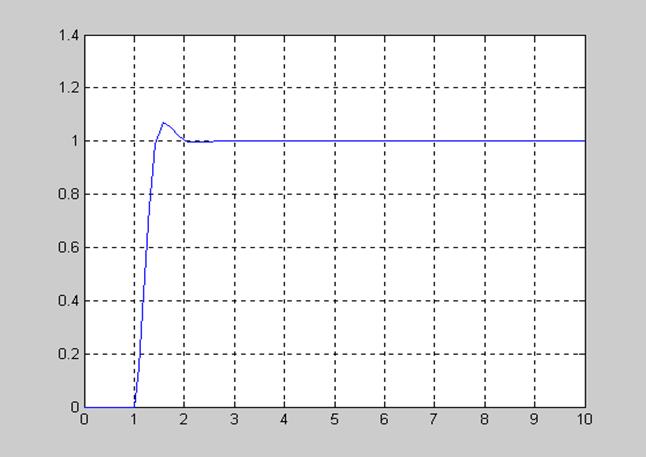
Передаточную функцию нашей замкнутой системы 2-го порядка мы можем записать как дифференциальное уравнение 2-го порядка:
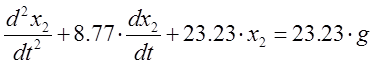
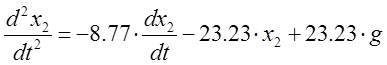
Это и есть наше 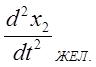 .
.
Теперь на основе этого уравнения подставим в уравнение (3) это желаемое уравнение :
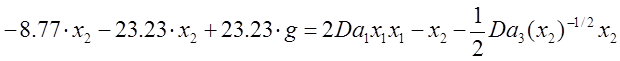
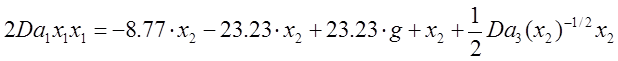
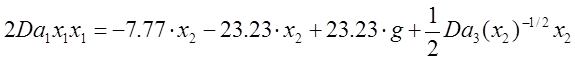
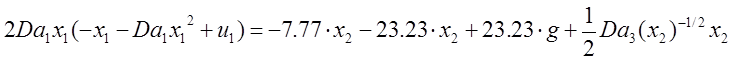
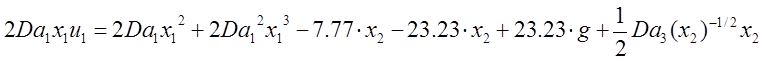
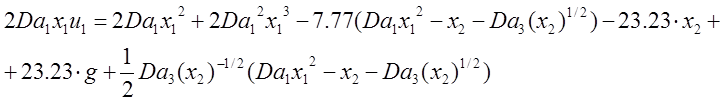
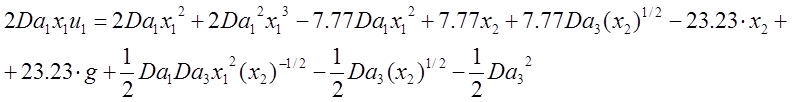
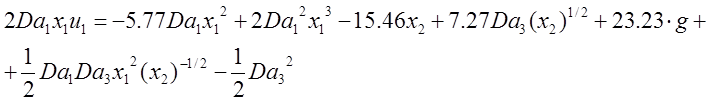
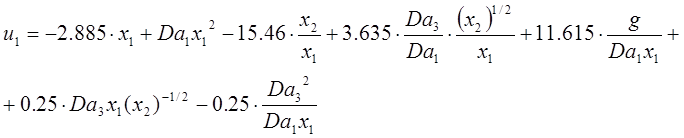
Получили закон для управляющего
воздействия, которое включает задающее воздействие g, где ![]() ¾ числа Дамкелера для разных ступеней реакции.
¾ числа Дамкелера для разных ступеней реакции.
Зададимся параметрами химического реактора :
V = 10 м3 ¾ объем химического реактора;
t = 30 мин =1800 с ¾ время протекания реакции;
F = V/t = 0.00555 м3/с =5.55 л/с;
Причем константы скоростей реакции зависят от температуры :
![]() , i=1,2 где Ei ¾ энергия активации; Ai0 ¾ концентрации реагентов.
, i=1,2 где Ei ¾ энергия активации; Ai0 ¾ концентрации реагентов.
А10 = 4000 л/(моль×с) = 4 м3/(моль×с),
А20 = 6.2×105 л/(моль×с) = 6.2×102 м3/(моль×с),
Е1 = 5000 кал/(г×моль),
Е2 = 10000 кал/(г×моль).
Подставив значения, приняв Т=300 °С, получим :
![]()
![]()
Получим управляющее воздействие равным :
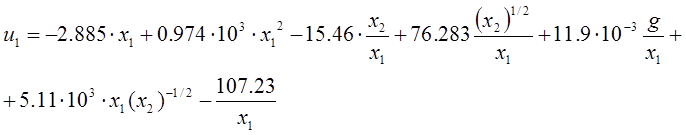
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.