Задачи, которые до сих пор возлагали на 1 центральный ЭВМ, теперь распределяется по нескольким специализированным микровычислителям. Децентрализованные системы позволяют снизить требования к быстродействию отдельных вычислителей, рассредоточить и упростить прикладное программное обеспечение, повысить стойкость к отказам и устранить основные недостатки, свойственные системам с центральным ЭВМ.
С 1975г в промышленность поступили цифровые регуляторы и программируемые системы управления. Одна цифровая машина может выполнять функции нескольких аналоговых, могут реализовывать дополнительные функции, выполнявшие раннее другими устройствами или совершенно новыми формами (программированную проверку номинальных режимов, автоматический переход к обработке регулятора, осуществляющую по разомкнутому циклу в соответствии с текущим режимом работы системы, контроль предельных значений сигналов и т.д.).
На основе цифровых регуляторов могут быть построены системы управления любых типов, включая системы с последовательным управлением, многомерные системы с перекрестными связями, системы с прямыми связями. Таким образом, перечисленное позволяет утверждать, что цифровые измерительные и управляющие технологии со временем получат самое широкое распространение и в значительной степени вытеснят традиционную аналоговую технику.
Большой интерес представляет так же сравнительное исследование цифровых и непрерывных систем с целью анализа эффектов вносимых квантованием сигналов по времени и по уровню. Что и будет рассмотрено далее в курсовой работе.
1. ПРЕОБРАЗОВАНИЕ НЕПРЕРЫВНОЙ МОДЕЛИ В ДИСКРЕТНУЮ И ВЫБОР ПЕРИОДА КВАНТОВАНИЯ
Каждую систему управления, в которой присутствует хотя бы один элемент, который не подчиняется непрерывному характеру изменения сигналов можно отнести к классу дискретных систем. Для этих систем характерным является исчезновение сигналов информации хотя бы на одном элементе на небольшой отрезок времени.
Пусть
имеем на входе в дискретный элемент непрерывный сигнал. .В этом случае
реальное время заменяем на кванты и вводим период квантования t=к×Т, к=0,1,…,![]() . Если Т
. Если Т![]() 0
тогда имеем непрерывную модель.
0
тогда имеем непрерывную модель.
Непрерывную систему, структурная схема которой приведена
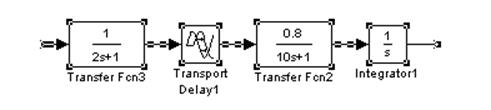
необходимо перевести в дискретную область. Для этого выбрать период квантования. Известно, что период квантования должен быть кратен запаздыванию. В этом случае выберем Ткв =1,0.2,0,1 ( что кратно 0,2 ).Перед переводом в дискретную область, перемножаем передаточные функции объектов.
Воспользуемся приложением Simulink математического пакета MATLAB.
WW1=tf([1],[2 1],'td',0.2);
2=tf([0.8],[10 1 0]);
w1w2=W1*W2
Transfer function:
0.8
exp(-0.2*s) * ------------------20 s^3 + 12 s^2 + s
W=c2d(w1w2,1)
Transfer function:
0.003035 z^3 + 0.01942 z^2 + 0.007474 z + 3.017e-005
---------------------------------------------------z^4 - 2.511 z^3 + 2.06 z^2 - 0.5488 z
Sampling time: 1
WWW=c2d(w1w2,0.1)
Transfer function:
6.568e-006 z^2 + 2.588e-005 z + 6.374e-006
z^(-2) * -----------------------------------------z^3 - 2.941 z^2 + 2.883 z - 0.9418
Sampling time: 0.1
WW=c2d(w1w2,0.2)
Transfer function:
5.177e-005 z^2 + 0.000201 z + 4.875e-005
z^(-1) * ---------------------------------------z^3 - 2.885 z^2 + 2.772 z - 0.8869
Sampling time: 0.2
В результате перехода в дискретную область получаем следующий график, на котором отображены функции перехода с различным временем квантования.
2. МОДЕЛИРОВАНИЕ ДИСКРЕТНОГО ВАРИАНТА ОБЪЕКТА И НАХОЖДЕНИЕ ОШИБКИ ДИСКРЕТИЗАЦИ
Структурная схема объекта в непрерывной области и дискретной области.
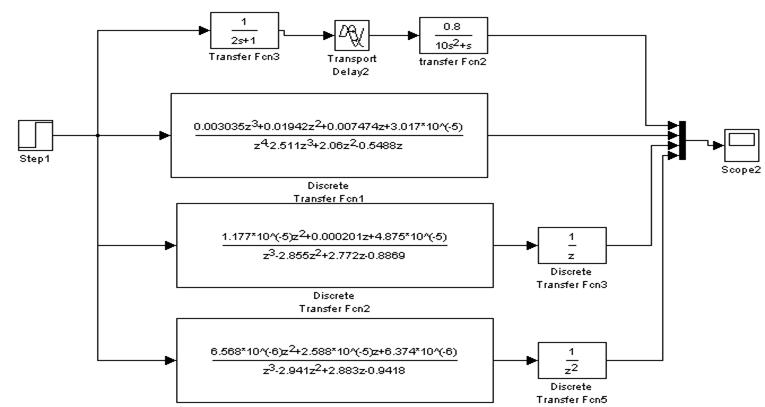
При моделировании системы и последующем анализе пришли к выводу что наиболее оптимальный вариант достигается при шаге квантования равном1, при этом график выглядит следующим образом:
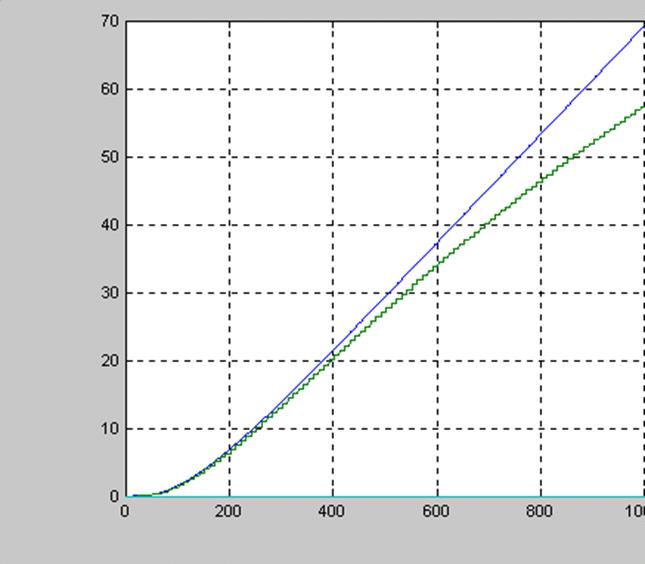
Так как передаточная функция объекта нашей системы в своей структуре
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.